场景文本检测&识别学习 day09（SSM、S4、Mamba、S6）

本文链接：https://blog.youkuaiyun.com/u011453680/article/details/138823482

在这里插入图片描述

SSM是一个针对连续函数的模型，即输入是连续函数，输出也是连续函数。
上图为状态方程和输出方程，其中h(t)是当前时刻的状态，x(t)是当前时刻的输入，h’(t)是下一个时刻的状态，y(t)是当前时刻的输出。于是上图可以写成下图的形式：
下面是详细的流程图，由于D * x(t)为跳跃连接（res连接），所以在论文中一般都省略，灰色部分为通常意义上的SSM模型流程部分
综上，SSM的方程可以写成以下的形式：
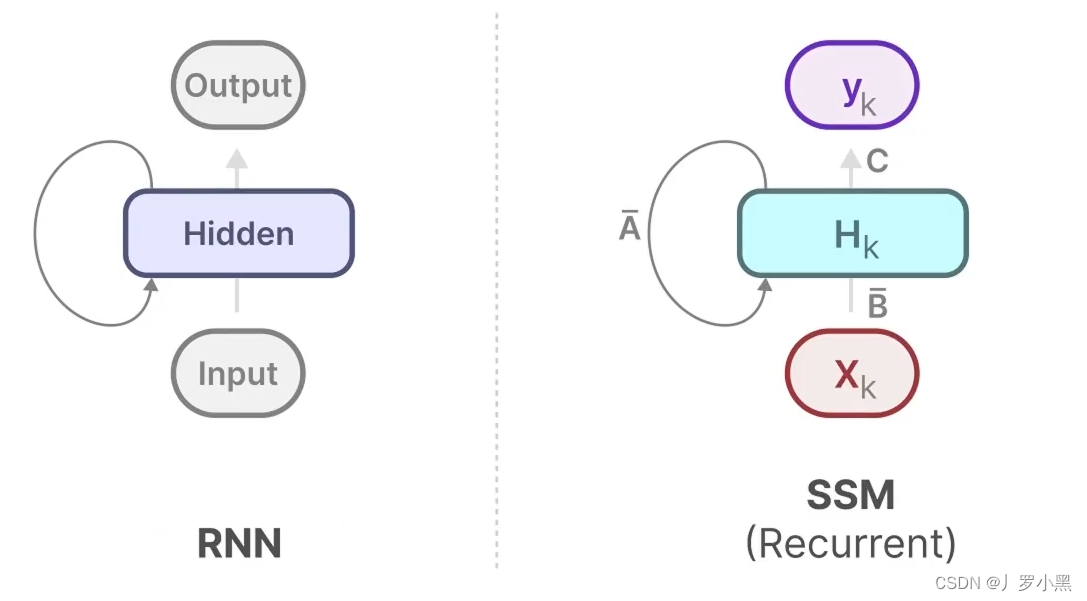
由此可以得出SSM跟RNN很类似，一个拥有状态，一个拥有隐藏状态，如下：

S4模型对SSM的改进有以下三点：
1. 采用零阶保持，来进行连续化：由于SSM模型是针对连续函数的，但是在文本、图像等领域，数据都是离散的，所以我们需要将离散的点连续化，才能输入进SSM模型，最后再从连续的输出中采样离散的点来得到真正的输出
2. 使用卷积结构表示，从而能够并行训练，加快训练速度
3. 使用HIPPO矩阵，解决长距离依赖
先看零阶保持，如下：
对于离散输入，在每个时间步 $\Delta$ 中，都保持到一个位置上，从而可以使输入连续
对于连续输出，每隔一个时间步 $\Delta$ ，都进行一个采样，从而可以得到离散输出
由于只有A、B矩阵是反应之前状态、输入是如何影响当前状态的（在连续模型中），而C矩阵是反应状态和输出的映射关系（在连续模型和离散模型中是相同的），所以离散化的重点就是离散化那些描述状态是如何随时间改变的连续模型的矩阵，即A、B矩阵。A、B矩阵是常数。
注意：矩阵可以乘函数，但是这个函数得是向量值函数，通常是用来表示系统状态。
相对应的离散化A、B矩阵如下：
那么状态方程和输出方程就变成如下的形式，为了简化，现在的 $h_k$ 表示当前的状态， $h_(k-1)$ 表示之前的状态， $y_k$ 表示当前的输出， $x_k$ 表示当前的输入
再看卷积结构表示，如下：
如果我们递归的将 $h_t$