Finding Nemo
| Time Limit: 2000MS | Memory Limit: 30000K | |
| Total Submissions: 6880 | Accepted: 1576 |
Description
Nemo is a naughty boy. One day he went into the deep sea all by himself. Unfortunately, he became lost and couldn't find his way home. Therefore, he sent a signal to his father, Marlin, to ask for help.
After checking the map, Marlin found that the sea is like a labyrinth with walls and doors. All the walls are parallel to the X-axis or to the Y-axis. The thickness of the walls are assumed to be zero.
All the doors are opened on the walls and have a length of 1. Marlin cannot go through a wall unless there is a door on the wall. Because going through a door is dangerous (there may be some virulent medusas near the doors), Marlin wants to go through as few doors as he could to find Nemo.
Figure-1 shows an example of the labyrinth and the path Marlin went through to find Nemo.
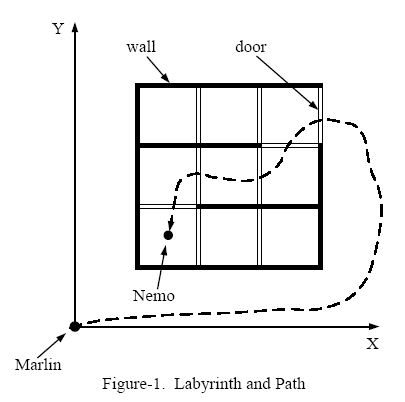
We assume Marlin's initial position is at (0, 0). Given the position of Nemo and the configuration of walls and doors, please write a program to calculate the minimum number of doors Marlin has to go through in order to reach Nemo.
After checking the map, Marlin found that the sea is like a labyrinth with walls and doors. All the walls are parallel to the X-axis or to the Y-axis. The thickness of the walls are assumed to be zero.
All the doors are opened on the walls and have a length of 1. Marlin cannot go through a wall unless there is a door on the wall. Because going through a door is dangerous (there may be some virulent medusas near the doors), Marlin wants to go through as few doors as he could to find Nemo.
Figure-1 shows an example of the labyrinth and the path Marlin went through to find Nemo.

We assume Marlin's initial position is at (0, 0). Given the position of Nemo and the configuration of walls and doors, please write a program to calculate the minimum number of doors Marlin has to go through in order to reach Nemo.
Input
The input consists of several test cases. Each test case is started by two non-negative integers M and N. M represents the number of walls in the labyrinth and N represents the number of doors.
Then follow M lines, each containing four integers that describe a wall in the following format:
x y d t
(x, y) indicates the lower-left point of the wall, d is the direction of the wall -- 0 means it's parallel to the X-axis and 1 means that it's parallel to the Y-axis, and t gives the length of the wall.
The coordinates of two ends of any wall will be in the range of [1,199].
Then there are N lines that give the description of the doors:
x y d
x, y, d have the same meaning as the walls. As the doors have fixed length of 1, t is omitted.
The last line of each case contains two positive float numbers:
f1 f2
(f1, f2) gives the position of Nemo. And it will not lie within any wall or door.
A test case of M = -1 and N = -1 indicates the end of input, and should not be processed.
Then follow M lines, each containing four integers that describe a wall in the following format:
x y d t
(x, y) indicates the lower-left point of the wall, d is the direction of the wall -- 0 means it's parallel to the X-axis and 1 means that it's parallel to the Y-axis, and t gives the length of the wall.
The coordinates of two ends of any wall will be in the range of [1,199].
Then there are N lines that give the description of the doors:
x y d
x, y, d have the same meaning as the walls. As the doors have fixed length of 1, t is omitted.
The last line of each case contains two positive float numbers:
f1 f2
(f1, f2) gives the position of Nemo. And it will not lie within any wall or door.
A test case of M = -1 and N = -1 indicates the end of input, and should not be processed.
Output
For each test case, in a separate line, please output the minimum number of doors Marlin has to go through in order to rescue his son. If he can't reach Nemo, output -1.
Sample Input
8 9 1 1 1 3 2 1 1 3 3 1 1 3 4 1 1 3 1 1 0 3 1 2 0 3 1 3 0 3 1 4 0 3 2 1 1 2 2 1 2 3 1 3 1 1 3 2 1 3 3 1 1 2 0 3 3 0 4 3 1 1.5 1.5 4 0 1 1 0 1 1 1 1 1 2 1 1 1 1 2 0 1 1.5 1.7 -1 -1
Sample Output
5 -1
Source
题意:
给你坐标系中墙或门的位置,以及被困者的位置,问救援者从外面营救被困者至少通过几道门
代码:
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<string>
#include<queue>
#define MAX 210
#define INF 0x3f3f3f3f
using namespace std;
typedef struct Node
{
int x,y,len;
bool operator < (const Node &x1) const //这道题运用了优先队列,len最小值优先
{
return len>x1.len;
}
}node;
int m,n,xmax,ymax,sx,sy;
int dis[MAX][MAX],xx[MAX][MAX],yy[MAX][MAX]; //dis[i][j]存放走到(i,j)点经过的门数
//xx[i][j]存放横向的墙或门的位置
//yy[i][j]存放纵向的墙或门的位置
priority_queue<node> q;
void bfs()
{
int x,y;
memset(dis,INF,sizeof(dis));
while(!q.empty()) q.pop();
node p;
p.x=0; p.y=0; p.len=0;
q.push(p);
dis[0][0]=0;
while(!q.empty())
{
p=q.top();
q.pop();
x=p.x; y=p.y;
if(x==sx && y==sy) return;
if(y+1<=ymax && dis[x][y+1]>dis[x][y]+xx[x][y+1]) //向上走
{
dis[x][y+1]=dis[x][y]+xx[x][y+1];
p.x=x; p.y=y+1; p.len=dis[x][y+1];
q.push(p);
}
if(y-1>=0 && dis[x][y-1]>dis[x][y]+xx[x][y]) //向下走
{
dis[x][y-1]=dis[x][y]+xx[x][y];
p.x=x; p.y=y-1; p.len=dis[x][y-1];
q.push(p);
}
if(x-1>=0 && dis[x-1][y]>dis[x][y]+yy[x][y]) //向左走
{
dis[x-1][y]=dis[x][y]+yy[x][y];
p.x=x-1; p.y=y; p.len=dis[x-1][y];
q.push(p);
}
if(x+1<=xmax && dis[x+1][y]>dis[x][y]+yy[x+1][y]) //向右走
{
dis[x+1][y]=dis[x][y]+yy[x+1][y];
p.x=x+1; p.y=y; p.len=dis[x+1][y];
q.push(p);
}
}
dis[sx][sx]=-1;
}
int main()
{
int i,j,x,y,t,d;
double tx,ty;
while(scanf("%d%d",&m,&n)!=EOF)
{
if(m==-1 && n==-1) break;
xmax=-1; ymax=-1;
//memset(dis,INF,sizeof(dis));
memset(xx,0,sizeof(xx));
memset(yy,0,sizeof(yy));
for(i=1;i<=m;i++)
{
scanf("%d%d%d%d",&x,&y,&d,&t);
if(d)
{
for(j=0;j<t;j++)
yy[x][y+j]=INF;
xmax=max(x,xmax);
ymax=max(y+t,ymax);
}
else
{
for(j=0;j<t;j++)
xx[x+j][y]=INF;
xmax=max(x+t,xmax);
ymax=max(y,ymax);
}
}
for(i=1;i<=n;i++)
{
scanf("%d%d%d",&x,&y,&d);
if(d) yy[x][y]=1;
else xx[x][y]=1;
}
scanf("%lf%lf",&tx,&ty);
if(tx>xmax || ty>ymax) printf("0\n"); //注意这个判断条件
else
{
sx=(int)tx;
sy=(int)ty;
bfs();
printf("%d\n",dis[sx][sy]);
}
}
return 0;
}
思路:
bfs+优先队列
(这个优先队列要再研究下。。)





















 920
920

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








