CSU Warm Up 2

最新推荐文章于 2020-10-28 13:23:23 发布

Lanifer

最新推荐文章于 2020-10-28 13:23:23 发布

阅读量583

点赞数

CC 4.0 BY-SA版权

本文链接：https://blog.youkuaiyun.com/lg_csu/article/details/15946083

本文提供了ACM竞赛中五个问题的代码实现与解析，涉及图论、字符串处理、动态规划等算法，通过具体实例展示了算法设计与编程技巧。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

比赛地址：http://acm.hust.edu.cn/vjudge/contest/view.action?cid=36773#status//G/0

先贴个代码 , 晚上再写题解 . 代码较挫，莫见笑

A: 诶，图论基本不会做，在高人提示下做出来的。

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cstdlib>
using namespace std;
const int maxn = 10050 , maxm = 100050;
int N , M  ,A ,E;
struct Edge{
    int u , v ,w;
    bool operator < (const Edge & b) const {
        return  w < b.w;
    }
}edge[maxm];
int fa[maxn] ;
int Find(int x){
    return fa[x]==x ? x : fa[x] = Find(fa[x]) ;
}

void Init(){
    for(int i= 0 ;i<=N;i++) fa[i] =  i;
}
int Kruskal(){
    int ans = 0;
    sort(edge , edge+E);
    for(int i=0;i<E;i++){
        int fx = Find(edge[i].u) , fy = Find(edge[i].v);
        if(fx == fy) continue;
        fa[fx] = fy ;
        ans += edge[i].w;
    }
    return ans;
}

int main()
{ 
    int T ,cas = 1;
    scanf("%d",&T);
    while(T--){
        scanf("%d%d%d",&N,&M,&A) ;
        Init();
        E = 0;
        int x ,y , z;
        for(int i=0;i<M;i++){
            scanf("%d%d%d",&x , &y , &z);
            if(z >= A) continue;
            edge[E++] = (Edge) {x , y ,z };
        }
        int cost = Kruskal();
        int cnt = 0;
        for(int i=1;i<=N;i++)
            if(Find(i) == i) cnt ++;
        cost += cnt * A;
        printf("Case #%d: %d %d\n",cas++ , cost , cnt);
    }
    return 0;
}

B : 略

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <string>
using namespace std;

int main()
{
    int T , cas = 1;
    char a[100] ,b[100];
    scanf("%d\n",&T);
    while(T--){
        gets(a) ,gets(b);
        int len = strlen(b);
        string AA = (string) a;
        string BB = (string) b;
        if (AA == BB) { printf("Case %d: Yes\n",cas++); continue; }

        string B = (string) b;
        string A = "";
        for(int i=0; a[i]!='\0' ;i++){
            if(a[i]!=' ') A += a[i];
        }
        if(A==B) { printf("Case %d: Output Format Error\n",cas++) ; continue; }
        else { printf("Case %d: Wrong Answer\n",cas++); }
    }
    return 0;
}

C: 预处理出所有必败点，再二分查找答案啊。。。

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
using namespace std;
typedef long long LL;
const int maxn = 1000050;
int X1[maxn] , Y1[maxn] ;
int vis[maxn];
int FN = 0;
int Find(int x1,int x2 ,int y1,int y2){
    int L = max (lower_bound(X1,X1+FN,x1)-X1 , lower_bound(Y1,Y1+FN,y1)-Y1);
    int R = min (upper_bound(X1,X1+FN,x2)-X1 , upper_bound(Y1,Y1+FN,y2)-Y1);
    return L < R ? R - L : 0 ;
}
LL gcd(LL a,LL b){
    LL r;
    while(b) r=a%b , a=b ,b=r;
    return a;
}
int main()
{
    for(int a=1,t=1;a<maxn;a++ ){
        if(vis[a]) continue;
        int b=a + t++;
        if(b>maxn) break;
        vis[a] = vis[b] = 1;
        X1[FN] = a , Y1[FN++] = b;
    }
    int T ,cas=1;
    scanf("%d",&T);
    while(T--){
        int x1, y1 ,x2 ,y2;
        scanf("%d%d%d%d",&x1, &y1 , &x2 , &y2);
        LL B = Find(x1,x2,y1,y2) + Find(y1,y2,x1,x2);
        LL C = (LL)(x2-x1+1)*(y2-y1+1) , A = C - B;
        LL d =gcd(A , C);
        A/=d , C/=d;
        printf("Board %d: %lld / %lld\n",cas++ , A , C);
    }
    return 0;
}

D: 略

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <map>
#include <string>
using namespace std;
typedef unsigned long long LL;
int B,V;
int t[300];
string name[300];

LL toNum(char* s){
    LL ret = 0;
    int len = strlen(s);
    for(int i=0 , t=len-1 ; t>=0 ;i++ ,t--){
        if(s[t]=='1') ret += (1<<i);
    }
    return ret;
}
int main()
{
    while(scanf("%d%d",&B,&V)!=EOF){
        map<string,LL> mp;
        for(int i= 0 ;i<V;i++){
            cin>>name[i];
            cin>>t[i];
        }
        char tmp[50];
        for(int i=0;i<V;i++){
            LL ret = 0;
            for(int j=0;j<t[i];j++){
                cin>>tmp;
                ret = (ret<<(B)) + toNum(tmp) ;
            }
            mp[name[i]] = ret;
        }

        int Q;
        cin>>Q;
        string tt;
        for(int i=0;i<Q;i++){
            cin>>tt;
            if(mp.find(tt) == mp.end()) {
                cout<<tt<<"="<<endl; continue;
            }
            else{
                cout<<tt<<"="<<mp[tt]<<endl;
            }
        }
    }
    return 0;
}

E:大水题

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
const int maxn=110;
int w[maxn] ,  h[maxn] , N;
int main()
{
    int cas = 1;
    while(scanf("%d",&N)!=EOF){
        memset(w , 0 ,sizeof(w));
        memset(h , 0 ,sizeof(h));
        int x, y;
        bool OK = false;
        for(int i=0;i<N;i++){
            scanf("%d%d",&x,&y);
            if(x==y) OK = true;
            w[x] = h[y] =1;
        }
        if(OK) {
            printf("Case %d : %d\n",cas++ , 0); continue;
        }

        int MIN = 200;
        for(int i=0;i<=100;i++){
            for(int j=0;j<=100;j++){
                if(w[i] && h[j]){
                    MIN = min(MIN , abs(i-j));
                }
            }
        }
        if(MIN == 0) {
            printf("Case %d : %d\n",cas++ , 1);
        }
        else printf("Case %d : %d\n",cas++ , (MIN+1)/2);
    }
    return 0;
}

G: 此题可用LCS模型来解决，为了更好的说明，在此先复习一下最长公共子序列：

动态规划的一个计算最长公共子序列的方法如下，以两个序列 $X$ 、 $Y$ 为例子：

设有二维数组 $f[i][j]$ 表示 $X$ 的 $i$ 位和 $Y$ 的 $j$ 位之前的最长公共子序列的长度，则有：

$f[1][1] = same(1,1)$

$f[i][j] = max\{f[i-1][j-1] + same(i,j), f[i-1][j],f[i][j-1]\}$

其中， $same(a,b)$ 当 $X$ 的第 $a$ 位与 $Y$ 的第 $b$ 位完全相同时为“1”，否则为“0”。

此时， $f[i][j]$ 中最大的数便是 $X$ 和 $Y$ 的最长公共子序列的长度，依据该数组回溯，便可找出最长公共子序列。

该算法的空间、时间复杂度均为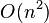 $O(n^{2})$

此题稍有不同的是：多了个"bad" , 且必须保证连续，故只需将状态转移改为：

dp[ i ][ j ] = dp[ i -1 ][ j-1 ] + 1 , if " s[i] and s[j] are not bad candies " && "s[ i ] == s[ j ] ";

dp[ i ][ j ] = 0 , otherwise;

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <string>
using namespace std;
const int maxn= 1010;
int dp[maxn][maxn];
int id(char c){
    if(c>='a' && c<='z') return c-'a';
    return c-'A' + 26 ;
}
char a[maxn] , b[maxn] ;
int isbad[100] , A[maxn] , tot;

int main()
{ 
    int T , cas=1;
    scanf("%d\n",&T);
    while(T--){
        memset(isbad,0,sizeof(isbad));
        memset(dp , 0, sizeof(dp));

        gets(a+1) , gets(b) ;
        int len = strlen(a+1) , len2 = strlen(b);
        for(int i=0;i<len2;i++){
            isbad[id(b[i])] = 1;
        }
        tot = -1;
        for(int i=1;i<=len;i++){
            int tmp = id(a[i]);
            if(isbad[tmp]) A[i] = tot--;
            else A[i] = tmp;
        }
        int ans = 0;

        for(int i=1;i<=len;i++){
            for(int j=i+1;j<=len ; j++ ){

                 if(A[i] < 0 || A[j] <0 ) {         // bad candies
                    dp[i][j] = 0;
                    continue;
                }
                if(A[i] == A[j] ){ 
                    dp[i][j] = dp[i-1][j-1] + 1;
                }
                else {
                    dp[i][j] = 0;
                }
                int MIN = min(dp[i][j] , j-i);  // 避免重叠
                ans = max (ans , MIN); 
            }
        }
        printf("Case #%d: %d\n",cas++ , ans);
    }

    return 0;
}