Ural 1268 Little Chu (原根)

最新推荐文章于 2022-02-20 02:53:10 发布

原创最新推荐文章于 2022-02-20 02:53:10 发布 · 1.6k 阅读

0 ·

CC 4.0 BY-SA版权

ACM_数论and数学类同时被 2 个专栏收录

55 篇文章

订阅专栏

ACM_Ural

5 篇文章

订阅专栏

本文介绍了一种高效求解质数n的最大原根的方法。通过分析原根的性质及利用快速幂模运算，提出了非暴力求解策略，显著提高了计算效率。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

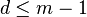对于两个正整数 $gcd(a,m)=1$ ，由欧拉定理可知，存在正整数 $d \le m-1$ ，比如说欧拉函数 $d= \phi (m)$ ，即小于等于 m 的正整数中与 m 互质的正整数的个数，使得 $a^d \equiv 1 \pmod{m}$ 。

由此，在 $gcd(a,m)=1$ 时，定义 $a$ 对模 $m$ 的指数 $Ord_m(a)$ 为使 $a^d \equiv 1 \pmod{m}$ 成立的最小的正整数 $d$ 。由前知 $Ord_m(a)$ 一定小于等于 $\phi (m)$ ，若 $Ord_m (a) = \phi (m)$ ，则称 $a$ 是模 $m$ 的原根。

摘自维基百科

这个题目就是要求一个质数n的最大的原根

现在的问题就是怎么求原根，如果直接暴力是 O(nlogn * 因子数)，显然是不行的。。

方法：

如果q不是n的原根，那么必然存在一个t < n-1且 q^t = 1(mod n)，这里我就假设q^t = 1(mod n)， t肯定是整除n-1的(想想就明白)

根据裴蜀定理可知ax+by=gcd(a,b)必然有解

所以必然存在tx + (n-1)y = gcd(t, n-1)，所以q^(tx) = 1 = q^( -(n-1)y + gcd(t, n-1)) = q^( gcd(t, n-1) ) ，即q^( gcd(t, n-1) ) = 1

因为t < n-1 且t 整除n-1，所以 t 至少整除 (n-1)/pi (1 <= i <= tot)中的一个，pi为n-1的素因子

所以要判断q是不是n的原根，只需要判断 q^( (n-1)/pi ) % n 其中如果有一个等于1的话，那q就不是原根！

代码：

#include 
  
   
#include 
   
    
#include 
    
     
using namespace std;
typedef __int64 ll;

int a[111];

int pow_mod(int x, int n, int mod) {
    int ret = 1;
    while(n) {
        if(n & 1)   ret = (ll)ret*x%mod;
        x = (ll)x*x%mod;
        n >>= 1;
    }
    return ret;
}

int main() {
    int n, t;
    scanf("%d", &t);
    while(t--){
        scanf("%d", &n);
        int tmp = n-1, tot = 0;
        for(int i = 2;i*i <= tmp ;i++) if(tmp % i == 0) {
            a[tot++] = i;
            while(tmp % i == 0) tmp /= i;
        }
        if(tmp > 1) a[tot++] = tmp;
        tmp = n-1;
        for(int i = n-1;i >=2; i--) {
            bool flag = 1;
            for(int j = 0;j < tot; j++) {
                if(pow_mod(i, tmp/a[j], n) == 1) {
                    flag = 0; break;
                }
            }
            if(flag) {
                printf("%d\n", i); break;
            }
        }
    }
    return 0;
}