tensorflow基础学习—滑动平均模型_模型输出滑动平均-优快云博客

本文链接：https://blog.youkuaiyun.com/two_apples/article/details/97138289

本文深入探讨了滑动平均模型在TensorFlow中的应用，详细解释了指数加权平均算法及其在模型训练中的作用，包括影子变量的概念和如何通过动态调整衰减率加速训练过程。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

滑动平均模型可以再一定程度上提高最终模型在测试数据上的表现，下面来说说我对它的理解。

下面来介绍一下google 关于滑动平均模型的原话介绍：

在tensoreflow中提供了tf.train.ExponentialMovingAverage来实现滑动平均模型。在初始化ExponentialMovingAverage时，需要提供一个衰减率（decay）。这个衰减率将用于控制模型更新的速度。ExponentialMovingAverage对每个变量会维护一个影子变量（shadow_variable），这个影子变量的初始值就是相应变量的出事值，而每次运行变量更新时，影子变量就会更新为: $shadow\_variable=decay * shadow\_variable+(1-decay) * variable$ 其中shadow_variable为影子变量，variable为待更新的变量,decay为衰减率，从公式可以看到，decay决定模型更新的速度，decay越大，模型越趋于稳定，在实际运用中，decay一般都是很接近1的数字（比如0.99或者0.999）。为了使模型在训练前期可以训练的更快，ExponentialMovingAverage还提供了num_updates参数来动态设置decay的大小，如果ExponentialMovingAverage初始化时提供了num_dates参数，那么每次更新使用的衰减率就是： $min\{decay,\frac{1+num\_updates}{10+num\_updates}\}$ 以上的官方阐述到此结束，其实看完这段话还不足以理解，但是需要先get到几个关键词，衰减率，影子变量，num_dates可以在训练前期训练的更快。解释部分开始：

第一，我们需要了解指数加权平均算法，其实影子变量的更新公式就是利用的指数加权算法。

指数加权推导与偏差修正

以上是一个链接，有一个数学推导的过程，这里我在通俗的解释一下什么指数加权：
指数加权平均，也叫指数加权移动平均，有两个作用，一是抚平短期波动，二是显现变化趋势，以气温为例：
加权平均的计算公式： $T_t=\beta\ T_{t-1}+(1-\beta)\ \theta_t$ 其中 $T_t$ 表示第t天的记录温度， $\theta$ 表示第t天的测量温度，经过加权后，温度曲线会更加的平滑， $\beta$ 越大，后项收到前项的影响就会越大。指数加权经数学证明为 $\frac{1}{1-\beta}$ 个数据的平均移动。假设 $\beta=0.9$ ,即是今天的测量温度对记录温度的贡献为0.1。
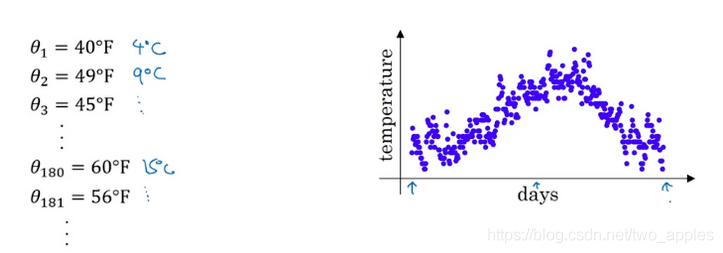
在这里插入图片描述
初始化 $T_t=0,\beta=0.9$ 时
$T_1=\beta\ T_0+(1-\beta)\ \theta_1$ $T_2=\beta\ T_1+(1-\beta)\ \theta_2$ $T_3=\beta\ T_2+(1-\beta)\ \theta_3$ $\dots$ 将 $T_{100}$ 展开得到 $T_{100}=0.1\theta_{100}+0.9*T_{99}=0.1\theta_{100}+0.9*(0.1\theta_{99}+0.9*T_{98})$ $=0.1\theta_{100}+0.1*0.9\theta_{99}+0.1*0.9^2\theta_{98}+\dots+0.1*0.9^{99}\theta_1$ 这是一个衰减，以 $\frac{1}{e}$ 为界限，当变量前面的系数小于这个值时，我们可以看成这个变量对总量（即估算的气温）没有贡献，而只有系数大于 $\frac{1}{e}$ 的变量对气温估算有贡献，通过计算当 $\beta=0.9$ 时，一共有10项值有贡献， $\beta=0.98$ 时，有50项有贡献。即是有 $\frac{1}{1-\beta}$ 个数据有贡献，于是便有了下图：
当 $\beta=0.9$ 时，代表用最近10天的平均气温来估算（红色线）：
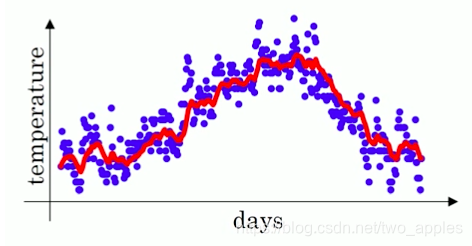
在这里插入图片描述
当 $\beta=0.98$ 时，代表用最近50天的平均气温来估算（绿色线），当 $\beta=0.5$ 时，代表用最近2天的平均气温来估算（黄·色线）：

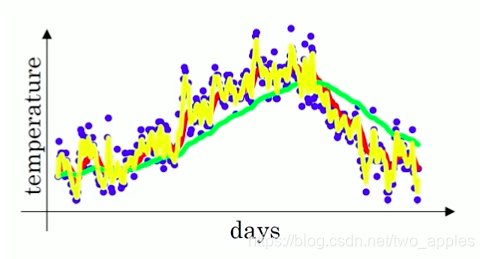
num_updates用来在前期控制衰减率，假如 $\beta=0.98$ ，但是在记录前期并没有50个数据来参考，估计值就会偏离，这也是指数平均法里面的偏差修正，但是在滑动平均模型里通过num_uptdates来控制衰减率。
$min\{decay,\frac{1+num\_updates}{10+num\_updates}\}$ 当num_updates比较小时，就会采用后面的那个作为衰减率。
当num_updates=5时， $\frac{1+num\_updates}{10+num\_updates}$ 值比较小，用于初期的衰减更加合适。
影子变量所谓影子变量就是通过滑动模型得到的值，当记录的数据出现较不符合规律的噪声时，影子变量回把它拉到一个比较正常的范围之内，其实我们真正要用的应该是影子变量，而不是记录的值，影子变量是趋势的刻写。

import tensorflow

#定义一个变量用于计算滑动平均,这个变量的初始值为0
#类型是tf.float32，因为所有需要计算滑动平均的变量必须是实数型

v1=tf.Variable(0,dtype=tf.float32)
#这里step变量模拟神经网络中迭代的轮数，可以用于动态控制衰减量，
# 需要用trainable=False参数指定不训练这个变量， 避免这个变量被计算滑动平均值
step=tf.Variable(0,trainable=False)

#定义一个滑动平均的类(class)。初始化时给定了衰减率（0.99）和控制
# 率的变量step。定训练轮数的变量可以加快训练前期的迭代速度
ema=tf.train.ExponentialMovingAverage(0.99,step)
#定义一个更新变量滑动平均的操作，这里需要给定一个列表，每次执行
#这个操作时，这个列表的变量就会被更新
maintain_averages_op=ema.apply([v1])
with tf.Session() as sess:
    #初始化所有变量
    init_op=tf.global_variables_initializer()
    sess.run(init_op)

    #通过ema.average(v1)获取滑动平均之后变量的取值，在初始化
    # 之后变量v1的值和v1的滑动平均都是0
    print(sess.run([v1,ema.average(v1)]))

    #更新step的值为10000
    sess.run(tf.assign(step,10000))
    #更新v1的值为10
    sess.run(tf.assign(v1,10))
    #更新v1的滑动平均值，衰减率为min{0.99,(1+step)/(10+step)=0.999}=0.99
    #所以v1的滑动平均值会被更新到0.99*4.5+0.01*10=4.555
    sess.run(maintain_averages_op)
    print(sess.run([v1,ema.average(v1)]))
    #输出[10.0,4.5549998]

    #再次更新滑动平均值,得到的滑动平均值为0.99*4.555+0.01*10=4.60945
    sess.run(maintain_averages_op)
    print(sess.run([v1,ema.average(v1)]))