新书上市 | 读完这本书，连初中生都能回答钱学森出的那个关于火箭发射的经典难题了！

有一个关于钱学森先生的故事广为人知，他从国外回国后在中国科技大学任教，曾在一次开卷考试中出过一道题“从地球上发射一枚火箭，绕过太阳再返回到地球上来，请列出方程求解。”

考试从上午八点半开始，直到中午还没有一个人交卷，中间还有两个学生晕倒被抬出去。钱老宣布说：“吃午饭吧，吃完接着考。”直到傍晚也做不出来，大家只好交卷。成绩出来，竟有95％的人不及格。

通过这样一次考试，钱老认识到大家的数学基础不够，于是决定，力学系的毕业生延迟半年毕业，专门补习数学，所用教材就是加州理工学院的《工程数学》。在半年时间里，每个学生光数学题就做了3000多道。由于打下了坚实的数学基础，学生们受益匪浅。

时隔今日，知乎航天及天文学领域优秀答主太空僧给我们带来了他的新作《数理化，上天啦：如何把大象送上火星？》，这本书以一次假想的太空发射任务为线索，融合数理化等多学科领域的知识，深入全面地科普了火箭制造、推进剂、飞行入轨行等三方面的内容。

既有航天知识的科普，又有数理化知识的专业讲解，设计火箭、选择推进剂、飞船变轨转向、在火星生活……本书会事无巨细地教给你，如何进行一场穿越太空的行星际旅行。

来源 | 《数理化，上天啦（上）：如何把大象送上火星？》

作者 | 太空僧

节选自 | 火箭为什么要分好几级？

想把大象号火箭从地表送上轨道，至少要让它的速度达到 7.9 千米 / 秒的第一宇宙速度。那么，如何能让火箭加速到这么快呢？

01

能用大炮飞上天吗

很多物理科普读物在讲解质点在重力场中的运动轨迹时，都喜欢像上一节那样，举“牛顿大炮”的例子。但很少有人会追问：为什么是大炮而不是别的东西？

在 17 世纪，想要把一个物体以很高的初速度射出尽可能远的距离，加农炮是无可争议的首选。“加农”音译自意大利语“cannone”，意思是“大管子”。

大炮最早在中国宋朝后期就被发明出来了，欧洲在一两个世纪后也开始研制大炮，但准头都不太行，攻城时只能进行“范围攻击”，难言精准。直到伽利略和牛顿的时代，大炮才开始真正有了瞄准的概念。

后来，基于牛顿的数学和物理学体系，预测炮弹轨迹的“弹道学”才成为可能，大炮终于不再“瞎射”。可以说，是牛顿给大炮装上了“眼睛”，让其成为当时战场上最先进的武器装备。这也是牛顿在书中喜欢用大炮作为例子的原因之一。

直到 19 世纪中叶，科幻作家儒勒·凡尔纳（Jules Verne，1828—1905）在写《从地球到月球》时，还在幻想用大炮将“炮弹车厢”中的三位乘客送上月球。

到了第一次世界大战（简称“一战”）期间，大炮的初速度更高、射程更远了。1918 年 3 月 23 日早上 7 点 18 分，法国巴黎塞纳河畔突然遭到轰炸，整个巴黎的民众都听到了巨响。

仅仅过了约 20 分钟，巴黎东站附近再次遭受毫无预警的爆炸袭击。之后每隔 15~20 分钟，巴黎城区就会发生一起爆炸。那时同盟国已经研发出用于投弹的轰炸机，所以法国人自然而然地将这突如其来的轰炸归咎于此，于是紧急加强了防空和预警措施。

可是等了整整一天，巴黎上空也没出现一架德国的飞机，但莫名的巨响仍在继续——第一天共发生了 21 次爆炸。

巴黎城内人心惶惶，市民纷纷猜测德军已逼近巴黎，恐惧与不安如瘟疫般蔓延。摸不着头脑的法国军队在爆炸处搜集到一些弹片，这些厚度超过 5 厘米的弹片上有着明显的斜向凹凸线条，显然是大炮的膛线挤压痕迹。

当时的大炮射程有限，普遍在 10 千米 ~20 千米，于是法军在巴黎近郊展开了地毯式搜索，但一无所获。为了尽快找到躲在暗处的敌军大炮，法军启用了他们最新研发的声波监听定位设备。

尽管狡猾的德军为了掩盖巨响，在射击时安排其他地方的普通大炮同时发射，但法国的监听人员还是很快锁定了这门超级大炮的方位：在巴黎和拉昂的连线上。

然而，即使法军飞行员在拉昂附近的森林上空亲眼看到了大量的烟雾，也不敢相信轰击巴黎的炮弹来自那里，因为拉昂和巴黎相距 100 多千米，射程如此远的大炮超出了法国人的想象。

后来的情报表明，轰击巴黎的 300 多枚炮弹确实是从拉昂的这门名为“巴黎大炮”的大炮中射出的。作为一战时期最大的大炮，它能让炮弹的初速度达到惊人的 1640 米 / 秒，是声速的 4 倍多。射程达到 130 千米，能把 106 千克的炮弹打到 4.23 万米的高空。

这是当时人造物体所能达到的最大高度，以至于炮手在计算炮弹的落地位置时，必须考虑地球自转的影响。拉昂的纬度比巴黎更高，科里奥利力会让炮弹向右偏移，因此炮口实际要瞄准巴黎偏东的方向。

不过，由于受到空气阻力等各种因素的影响，偏差还是很大，实际轰炸效果因此大打折扣，几乎未能准确击中任何有价值的军事目标。

战争是肮脏血腥的。它消耗了巨大的社会资源，破坏了宝贵的文化遗产，甚至剥夺了无数无辜的生命。但从另一个角度来看，战争又能促进科技创新。各国倾注大量资金和人力，将科技的发展推向了极限。当然，我们绝不希望战争成为科技进步的最大动力。期待有一天，科技能反过来抑制战争，减少伤亡和痛苦，重塑人类对文明的理解。

一战结束后，德国人已经将目光从大炮转移到火箭的研发上去了，但是威力巨大的大炮在战后仍被一些研究机构所青睐。20 世纪 60 年代初，美国在加勒比海上的巴巴多斯建造了一门口径达 16 英寸（约 406 毫米）、炮管长 36 米的超级大炮，以研究利用大炮发射卫星的可行性。

之所以选在巴巴多斯，是因为那里比美国本土更靠近赤道，可以让炮弹或卫星从地球自转中获得更大的初始速度，以达到更高的轨道高度。可惜的是，这个被称为“高海拔研究计划”（High Altitude  Research Project，HARP）的项目，最终还是没能把任何炮弹或卫星送上轨道。

这门竖起来比 10 层楼还高的大炮的最大发射速度虽然达到了 2.2 千米 / 秒，但仍远低于第一宇宙速度。

退一步说，即使真的造出了“轰”地一下把物体加速到第一宇宙速度的超级大炮，这个物体也得像铸铁弹丸一样结实才行，精密的仪器载荷和我们的大象号火箭恐怕都承受不了这样的加速度。

就拿人来举例吧，普通人在 5 倍重力加速度，或者说 5 个 g 时就会出现眩晕和恶心，6.5 个 g 时就会昏迷。即使是经过长期训练的特技飞行员和航天员，也只能在 12 个 g 的极限过载中坚持很短的时间。

在发射前我们暂时还不清楚大象能承受多大的过载，假设采用普通人能承受的 6 个 g 为标准，若物体以 60 米 / 秒2 的加速度均匀加速（取 g=10 米 / 秒2），那么为了能达到第一宇宙速度，就需要匀加速 132 秒。

如果这个超级大炮的炮管是直的，经过计算可知，炮管需要 520 千米长，几乎相当于从北到南横跨整个塔里木盆地。如果炮尾在天山山脉，那么炮口就已经架到昆仑山脉上了。这么长的炮管，还没发射就被自身的重量压塌了。

当然，我们可以在地下挖一条长长的隧道作为炮管，只不过这项工程也过于浩大了；或者改为环形加速，就像粒子加速器那样，但巨大的离心力又会带来新的问题。

看来，想要实现太空旅行，大炮这种在短时间内把物体加速到第一宇宙速度的路线似乎不太现实，必须换一种加速的思路。

02

航天之父的火箭方程

在“牛顿大炮”的假想实验中，隐含了一个前提：大炮的炮弹本身是无动力的，被射出炮口时的速度就是它的飞行速度，即炮弹只能依靠发射时的初速度来维持自身不坠落到地面上。想要让炮弹飞得足够远，就得让炮弹在炮管里面加速到足够快，因此需要把炮管做得足够长，这样炮弹才有可能被充分加速。但前面已经分析了，在现有技术条件下，这在工程上是不现实的。

既然大炮的方法行不通，那是否可以用一个较小但持续的加速度来把火箭慢慢加速到第一宇宙速度呢？第二次世界大战（简称“二战”）后期，纳粹德国转向了这种思路，尝试用不需要炮管的火箭代替大炮。火箭把推进剂“背”在身上，这样就可以一边飞一边喷出气体加速了。当喷气产生的反作用力大于火箭所受的总重力时，合力向上，火箭就能加速上升。这样看来，似乎只要飞得足够久，就应该能达到第一宇宙速度。

当我们开车去长途旅行时，要去加油站加足够多的汽油才能到达目的地。火箭也一样，只是旅途中间没有加油站，而且油耗还挺高，所以火箭得背大量的推进剂才行。

问题来了，想要火箭飞得更远，就得背更多的推进剂，质量就增加了；质量增加后又需要消耗更多的推进剂，所以就得背更多推进剂……这就陷入了“面多加水，水多加面”的循环。人类现有的加工制造技术是有上限的，没办法无限制地增加质量，那到底要携带多少推进剂才刚好够用呢？想要得到答案，必须先找到速度增量与所需推进剂之间的关系才行。

然而，随着推进剂的不断消耗，火箭的质量是在不断变化的。这是一种变质量力学，我们无法直接套用牛顿第二定律来确定火箭的加速度和速度。只有另辟蹊径，才能解决这一难题。

1883 年，一位名叫康斯坦丁· 齐奥尔科夫斯基（Konstantin Tsiolkovsky，1857—1935）的俄国乡村教师也开始思考这一问题。他和戈达德一样，同为儒勒·凡尔纳的忠实读者，受其科幻小说的启发，齐奥尔科夫斯基自少年时代起就不断思考太空旅行的可行性，探究可变质量物体的运动理论。终于，在 1897 年 5 月10 日这一天，他找到了通往太空之门的钥匙。

在狭小逼仄的书房里，齐奥尔科夫斯基的脑海中浮现出一个广袤的宇宙。他先假设太空中有一枚不受任何外力影响的理想火箭。火箭的质量为m ，喷出气体的质量为dm，火箭因为喷出气体而得到了一个反作用力，所以速度增加了dv 。

为了计算方便，他假设喷气速度恒定不变为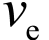，如图 1-14 所示。

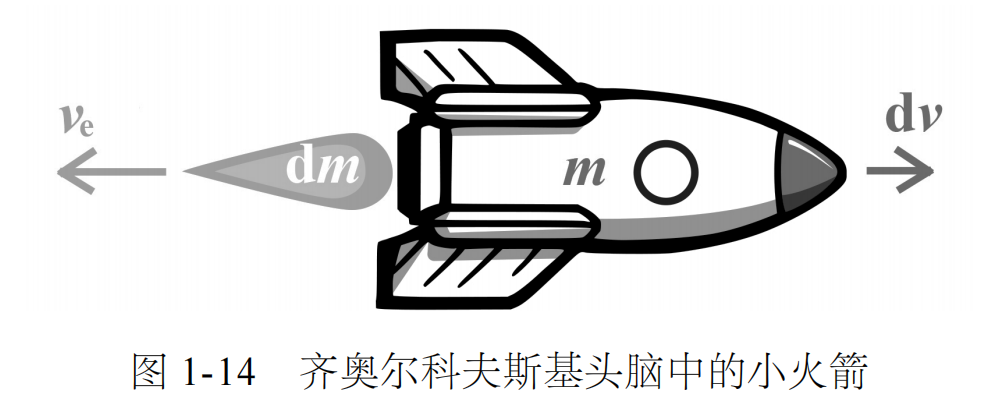
实际上，当后来的科学家造出真正的火箭后，发现在大气中飞行的火箭的实际喷气速度并不是恒定的，而是会随着外界大气压的变化而改变，且通常比在真空中的喷气速度小一些。

另外，在喷管出口的横截面上，各个点的喷气速度也不可能完全一致，但是具体的速度值又很难精确地测量出来。这也太复杂了！那怎么办？物理学家在分析问题时擅长化繁为简，抓主要矛盾。我们不妨把这个三维问题简化为一维问题，仍然假设一个均匀的轴向喷气速度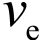 ，用这个假想的速度代替多变的实际喷气速度，使分析过程不至于过于繁杂。这个 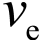便被称为“有效喷气速度”。

根据动量守恒定律，如果一个系统不受外力或所受外力的矢量和为零，这个系统的总动量保持不变，则有：

设开始喷气前，火箭的初始质量为 （包括推进剂、有效载荷和其他所有设备），速度为 。喷气完毕后（此时推进剂已所剩无几），火箭的最终质量变为 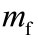。经过简单的微积分运算（具体的推导过程参考本节后的延伸阅读部分），齐奥尔科夫斯基得到了以下表达式：

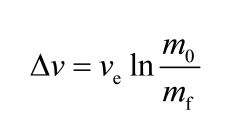
这就是后来以他的姓氏命名的“齐奥尔科夫斯基公式”，也被称为“齐奥尔科夫斯基火箭方程”。在不考虑空气阻力和地球引力等其他外力的理想情况下，利用这个公式能计算出火箭在发动机工作期间获得的速度增量。如果是从起飞到推进剂消耗完毕的整个过程，这个速度增量也被称为火箭的“特征速度”。

这个公式形式简单，应用起来也不难。举个例子，假设外太空中有一枚不受外力的初始质量为 3 吨的火箭，其发动机以 3 千米 / 秒的喷气速度向后喷气，最终消耗了 1 吨推进剂，那么火箭获得的速度增量为：

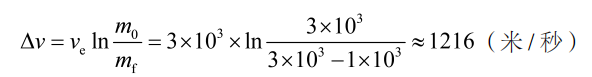
03

干质比与锤子

让我们再来看看下面这个公式：

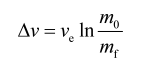
等式左边的速度差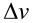 是火箭速度的变化量，如果从静止开始加速到彻底熄火结束，算出来的就是火箭的最终速度。从公式还可以看出，在喷出气体质量保持不变的情况下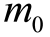（和 都不变），从静止开始加速的火箭的最终速度与等式右边的喷气速度 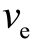成正比。

也就是说，火箭点火获得的最终速度取决于喷气速度，更快的喷气速度会得到更快的最终速度。这个结论符合我们的直觉，因此比较容易理解，至于如何才能让喷气速度更快，后面再详细讨论。

你只需要知道，不只是在齐奥尔科夫斯基的年代，即使是现在，最强大的化学火箭发动机喷气速度也不到 6 千米 / 秒。如果不想点办法，火箭根本不可能进入近地轨道。

我们先看公式的后半部分：火箭的最终速度与 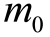和 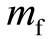的比值的对数成正比。火箭从地面发射时的总质量是 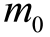，最后推进剂耗尽，只剩下有效载荷和不能抛弃的结构设备时的质量就是结构质量 。

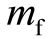从公式上来看，推进剂的需求量（ 与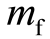 的差值）随着 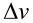的增加而呈指数级增加。或者说，为了让火箭的最终速度更快，火箭的初始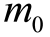质量 与最终质量 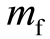的比值越大越好。这个比值有个专门的名称，叫作“干质比”。

不难看出，干质比越大，速度增量 越大，火箭能达到的最终速度也就越快。

04

从干质比到火箭分级

由于材料、技术和成本的限制，实际应用中的干质比是有上限的。我们无法造出一枚 99% 的质量是推进剂，只有 1% 的质量用于制造贮箱、发动机、整流罩的火箭，更何况还要考虑有效载荷的质量。因此，折中的方案就是火箭用掉多少推进剂，就把它对应的贮箱即时扔掉，避免带着无用的结构加速，浪费剩余的推进剂。

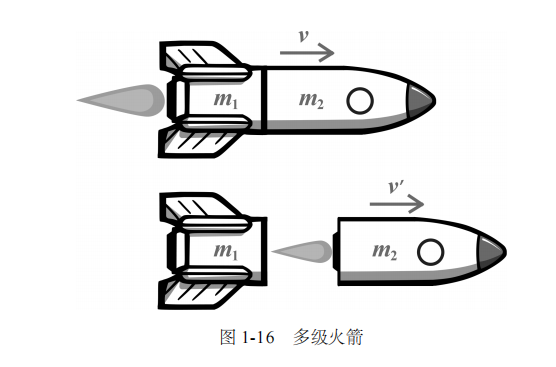
基于这个理论，齐奥尔科夫斯基提出了多级火箭的设想。他认为，通过多级火箭依次点火可以更容易地将有效载荷送入太空。一旦一级火箭的推进剂耗尽，就立即抛弃这一级的贮箱和发动机等结构，然后第二级火箭点火并继续加速剩余的箭体，如图 1-16 所示。

这种火箭分级的方法使最终质量变得更小，因此可以获得更快的最终速度。可以说，多级火箭是以尽可能低的成本将尽可能多的有效载荷送上太空的最具成本效益的策略。

为了更直观地展现单级火箭和多级火箭的差异，我们举个例子吧。假设火箭的喷气速度 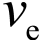为 3000 米 / 秒，考虑到空气阻力和重力的影响，我们计划让 达到略大于第一宇宙速度的 9000 米 / 秒。

如果用单级火箭 代入齐奥尔科夫斯基公式：

求得干质比为：

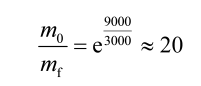
也就是说，初始质量是最终质量的 20 倍，那么推进剂质量占火箭初始质量的比就达到了 95%，剩余的 5% 分配给发动机、贮箱和有效载荷等。

航天飞机用于存放液氢−液氧推进剂的外储箱（那个让人印象深刻的大橙罐）所携带的推进剂的质量占比就达到了 96%，相比之下，苏打水易拉罐中的苏打水也只占到 94% 而已。

如果用两级火箭 第一级的喷气速度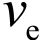 同样为 3000 米 / 秒，按照经验，假设第一级的推进剂耗尽后 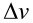只需要达到 4400 米 / 秒，按照同样的计算方法，求得干质比为：

因此第一级推进剂的质量占比约为 77%，剩余的质量占比为 23%。假设第一级火箭的贮箱和发动机等结构的质量占初始质量的 4%，则第一级火箭以外的质量占比为 19%。第一级被抛弃后，火箭的速度已经达到了 4400 米 / 秒，那么离最终目标速度 9000 米 / 秒还差的 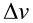是 4600 米 / 秒。再来一遍同样的计算过程，求得干质比为：

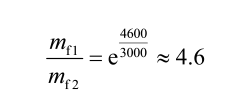
因此第二级推进剂的质量约占第二次点火前总质量的 78%，也就是约占发射前原始总质量的 15%（19%×78%），因此第二级火箭的贮箱、发动机以及有效载荷的质量占发射前总质量的 4%（100% – 77% – 4% – 15%）。

对于整个火箭来说，所有的发动机、贮箱和有效载荷的质量占比为4% + 4% = 8%，即推进剂质量占总质量的比下降到了 92%，而火箭的最终质量（抛弃第一级后只剩第二级，因此最终质量指的也是第二级的部分质量，如图 1-17所示）占比从 5% 下降至 4%。

4% 的数值意味着火箭的干质比从单级火箭的 20 提高到了现在的 25（100%/4%），即火箭分级这个方法让干质比变得更大了。从另一个角度来说，使用同样的推进剂，分级火箭可以产生更大的速度增量。

从上面的分析来看，似乎火箭级数越多，干质比越大，最终速度越快。但在实际应用中，火箭级数的增加意味着发动机、连接机构、伺服机构和控制机构的数量增加，这不但会让生产加工变得更为复杂，还会提高故障率和发射风险，如果想回收火箭的话也会变得更加困难，得不偿失。因此，目前的火箭多采用二到三级结构，最多不超过四级。

需要注意的是，齐奥尔科夫斯基火箭方程是一个理想化的模型，其成立需要满足两个前提条件：

1. 火箭本身不受外力，只受自身喷出气体产生的推力；

2. 火箭的喷气速度是恒定的。

在实际飞行中，火箭发动机可以通过调节阀门或其他技术保证喷气速度基本不变，但火箭毕竟是从地球发射的，它肯定会受到地球引力和空气阻力等一系列外力的影响。怎么办呢？难道齐奥尔科夫斯基火箭方程就不能用了吗？其实我们只要多试射几次，就能获得实际的数据，之后凭借经验，可以大致估算出这些外力的影响程度，再把这些影响折算成速度增量的损失值，齐奥尔科夫斯基火箭方程也就能在大气层内使用了。

  推荐阅读

《数理化，上天啦：

如何把大象送上火星？》

作者：太空僧

一本让孩子理解航天、爱上科学的科普佳作！

知乎航天及天文学领域优秀答主太空僧“手把手”地教你造火箭，去火星！

通过一个具体的场景：把大象送上火星，从第一步造火箭开始，到进入太空的过程，把数理化知识完美的与现实场景完美结合起来。设计火箭、选择推进剂、飞船变轨转向、在火星生活……本书会事无巨细地教给你，如何进行一场穿越太空的行星际旅行。