变态跳台阶

变态跳台阶

题目描述

一只青蛙一次可以跳上1级台阶，也可以跳上2级……它也可以跳上n级。求该青蛙跳上一个n级的台阶总共有多少种跳法。

题解

简要提炼思路：

1、有n个台阶，则每次可以跳1，2，3，，，n个台阶。【f(n)为n个台阶有多少种跳法】

2、若第一次跳1，2，3，，，n个台阶，则分别剩下n-1，n-2，n-3，，，0个台阶可以跳。

　　故有：　　   f(n) = f(n-1) + f(n-2) + ，，，+ f(1) + f(0) 　　（1）种跳法。

　　由此可得：   f(n-1) = f(n-2) + ，，，+ f(1) + f(0) 　　　　   （2）种跳法。

　　综合(1)(2) ：

　　　　　　　　

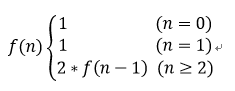
public int JumpFloorII(int target) {
        if(target <= 0 )
            return -1;
        else if(target == 1)
            return 1;
        else
            return 2 * JumpFloorII(target - 1);
}

参考详细解答：https://www.nowcoder.com/questionTerminal/22243d016f6b47f2a6928b4313c85387

posted @ 2019-03-08 18:35 sky-walker 阅读( ...) 评论( ...) 编辑 收藏