渐进符号
1、渐进紧确界记号:Θ
Θ的数学含义:
对一个给定的函数g(n),用Θ(g(n))来表示以下函数的集合
Θ(g(n))={ f(n):存在正常量c1、c2和n0,使得对所有n ≥ n0n_{0}n0,有0≤ c1g(n) ≤ f(n) ≤ c2g(n) }
Θ(g(n))要求每个成员 f(n)∈Θ(g(n)) 均渐进非负,即当n足够大时 f(n) 非负,渐进正函数就是对所有足够大的n均为正的函数。
EX:T(n)=100n4+20n3+15n2+6n+1100n^{4}+20n^{3}+15n^{2}+6n+1100n4+20n3+15n2+6n+1
当n足够大的时候,算法的运行时间取决于时间表达式T(n)的最高项,最高项的系数在n较大时,对时间作用较小,其余项可忽略不计.
故T(n)≈n4\approx n^{4}≈n4 T(n)=Θ(n4)T(n)= Θ(n^{4})T(n)=Θ(n4)
2、渐进上界记号:O
Θ记号渐进地给出一个函数的上界和下界,当只有一个渐进上界时,使用O记号。
数学定义:对于给定的函数g(n),用O(g(n))来表示以下函数的集合
O(g(n))={f(n)O(g(n)) = \{f(n)O(g(n))={f(n):存在正常数量n和c0c_{0}c0,使得对所有n⩾n0,0⩽f(n)⩽cg(n)}n\geqslant n_{0},0\leqslant f(n) \leqslant cg(n) \}n⩾n0,0⩽f(n)⩽cg(n)}
使用O记号,我们常常可以仅仅通过检查算法的总体结构来描述算法的运行时间,以插入排序为例,双重嵌套循环结构最坏情况运行为O(n2)(n^{2})(n2),也就是说上界为
O(n2)(n^{2})(n2)。
以下举几种常见的复杂度
O(1)<O(logn)<O(n)<O(nlogn)<O(n2)<O(n3)<O(2n)<O(n!)O(1)<O(logn)<O(n)<O(nlogn)<O(n^{2})<O(n^{3})<O(2^{n})<O(n!)O(1)<O(logn)<O(n)<O(nlogn)<O(n2)<O(n3)<O(2n)<O(n!)
O(1)O(1)O(1): 基本执行操作次数是常量
O(n)O(n)O(n): 一般出现在只有一个循环的情况下
O(n2)O(n^{2})O(n2):一般出现在嵌套循环中
public void test(int n)
{
for(int i=0;i<n;i++)
{
for(int j=0;j<n;j++)
{
......
}
}
}
O(logn)O(logn)O(logn):(二分查找等,例如以下模块 )
public void test(int n)
{
for(int i=1;i<n;i+=2)
{
.......
}
}
O(nlogn)O(nlogn)O(nlogn): 常出现在归并排序中
3、渐进下界符号:Ω
与O定义类似,Ω记号提供了渐进下界。
定理:对于任意两个函数f(n)和g(n)f(n)和g(n)f(n)和g(n),我们有f(n)=Θ(g(n))f(n)=Θ(g(n))f(n)=Θ(g(n)),当且仅当f(n)=O(g(n))且f(n)=ωf(n)=O(g(n)) 且 f(n)=\omegaf(n)=O(g(n))且f(n)=ω
4、非渐进紧确上界:o
由O记号提供的上界可能是也可能不是紧确的,非紧确的可用o记号。
定义:o(g(n))={f(n):对任意正常量c>0,存在常量n0>0,使得对所有的n⩾n0,有0⩽f(n)⩽cg(n)}o(g(n))=\{ f(n):对任意正常量c>0,存在常量n_{0}>0,使得对所有的n\geqslant n_{0},有0 \leqslant f(n) \leqslant cg(n)\}o(g(n))={f(n):对任意正常量c>0,存在常量n0>0,使得对所有的n⩾n0,有0⩽f(n)⩽cg(n)}
EX:f(n)=n2+n,o(n)=n3f(n)=n^{2}+n,o(n)=n^{3}f(n)=n2+n,o(n)=n3
5、非渐进紧确下界:ω\omegaω
ω和Ω\omega和\Omegaω和Ω的关系与o和O的关系相同,在这里不过多阐述。
可以用下图记忆渐进符号
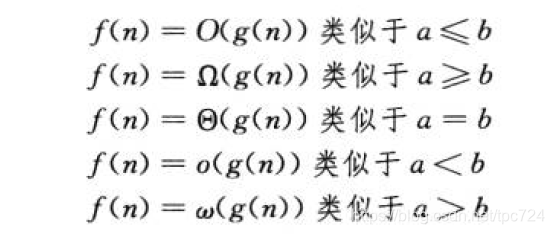
参考资料:算法导论(第三版)




 本文深入解析了算法分析中的渐进符号,包括Θ、O、Ω、o和ω的定义及应用,通过具体示例说明了如何使用这些符号来评估算法的时间复杂度。
本文深入解析了算法分析中的渐进符号,包括Θ、O、Ω、o和ω的定义及应用,通过具体示例说明了如何使用这些符号来评估算法的时间复杂度。
















 1489
1489

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








