The Difference Between Trees and Hash Tables

http://www.informit.com/guides/content.aspx?g=java&seqNum=472

ava Reference Guide

Hosted by Steven Haines

Guide Contents

•  Print

< Back  Page 47 of 650  Next >

The Difference Between Trees and Hash Tables

Last updated Mar 14, 2003.

Java provides two primary Set implementations: the TreeSet and the HashSet. Furthermore, it provides two primary Map implementations: the TreeMap and the HashMap. When would you want to use one over the other? What’s the difference?

The short answer is that the TreeMap and TreeSet classes store their data (or keys in the case of the TreeMap) in a Tree whereas the HashMap and HashSet store their data in a Hash Table. The longer, and more important answer, lies in the difference between a tree and a hashtable. The difference can be described in two ways: (1) implementation details and (2) behavior, where behavior describes the functionality that is available as well as the performance under different conditions.

I’ll start with the hash table. A hash table is a contiguous region of memory, similar to an array, in which objects are hashed (a numerical value is computed for the object) into an index in that memory. For example, consider a hash table that holds 100 elements. A hash function would compute a number between 0 and 99 and then insert the item at that location. When that item is requested then the same hash function would compute the same number and know exactly where to go to retrieve that object. There are some details that I’ve overlooked, such as sizing a hash table appropriately, the effect of resizing a hash table, and how to handle collisions (two objects hash to the same value), but I’ll address those as they come up. The key takeaways for using a hash table are:

• Inserting an object into a hash table is a constant time operation
• Retrieving an object from a hash table is a constant time operation

Trees, or more specifically binary search trees, store their data in hierarchical a tree. Figure 1shows an example of a tree.

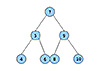
Figure 1. The Structure of a Tree

From figure 1, the top node is the “root” of the tree. The root has one child to its left and one child to its right, in which the child to its left has a lower value and the child to the right has a higher value. This requirement is maintained throughout the entirety of the tree. In this example, the root node has a value of 7: all of its left children are less than 7 and all of its right children are greater than 7. To add a new item to the tree, such as 3, we would examine the root node 7, see that 3 is less than 7, so we would go it its left child. The left child is 5, so we would again traverse to the left child. Finally, because 3 is less than 4, the new node is inserted as the left child of 4. A tree support inserting new elements at a speed that is of the order log(n), meaning that as long as the tree maintains its balance (each node has approximately the same number of children in its left subtree as in its right subtree), you will need to examine the logarithm (base 2) of the number of elements (n) contained within the tree.

Recall that log base 2 is defined as follows:

2^n = number of nodes

So in this case we have 7 nodes, so

2^n = 7, which is just a little under 3 (2^3 = 8)

This means that in order to find an object in a tree with 7 (or 8) nodes, you would need to examine 3 nodes. And the size of the tree grows rapidly with this exponent: 2^4 = 16, 2^5 = 32, 2^6 = 64, 2^7 = 128, and so on. If your tree has 128 elements, it will take 7 operations to find a location to insert a new item and it will take a maximum of 7 operations to find an object. It is not as fast as a hash table (constant time means one operation), but it is still rather fast.

And, as with hash tables, trees are not a panacea because you might have noticed that I added the caveat “as long as the tree maintains its balance.” Unfortunately great effort must be expended in order to keep a tree balanced, which complicates its implementation, but there are several well established algorithms to keep a tree balanced.

Given this background that hash tables store its data in an array like structure with constant time inserts, searches, and deletes and trees store its data in a hierarchical tree with log(n) inserts, log(n) searches, and log(n) deletes, when would you use one over the other?

Looking at performance alone, the hash table is the preferred data structure to hold your set and map data, but it has some significant drawbacks:

• It requires more memory than is needed to hold its data. This is true because as a hash table becomes more and more populated, the chances for collision (two objects hashing to the same index), become more and more likely. In general, a hash table should not be more than 75% - 80% full. This means that if you want to hold 100 items, you need to have a hash table that can hold 125 – 133 elements.
• You need to know approximately how many elements you want to hold in the hash table to avoiding having to resize the hash table. For example, consider a hash table that can hold 125 elements, has 100 elements and a load factor (how full it can become before it is resized) or 80%, and the 101st is added. The hash table has crossed that 80% threshold and must be resized: simply operation, right? Wrong! The hash function computes the index for an item in the table, based on the size of the table. Therefore, as the table is resized, to say 150, all 100 objects must be rehashed to an index between 0 and 149 (instead of the previous hash of values between 0 and 124.) Rehashing is very expensive operation that requires “n” operations – so when it occurs, your constant time insert becomes of order O(n), which is far worse than the performance of a tree.
• Because hash tables compute seemingly arbitrary values for objects, there is no way to extract objects in any natural order. For example, the numbers 1, 2, 3, and 4 may come out as 2, 1, 3, 4 or 4, 1, 3, 2 and so forth. The order is determined by where the hashing algorithm inserts the objects, not on any natural order

Contrasting hash tables with trees yields the following benefits that trees provide:

• Trees only use the amount of memory needed to hold its items
• Because trees can grow and shrink as needed, they never suffer from needing to be rehashed – the balancing operation may become complex, but at no point do the insert operation approach an order of O(n) (it never needs to examine every object in the tree during an insert)
• Because trees store objects in a hierarchical structure, it is simple to extract items in their natural order (as long as that natural order defines the condition by which the tree established its hierarchical structure.)

In short, if you know approximately how many items you need to maintain in your collection, you can maintain additional unused memory in order to avoid hash collisions, and you do not need to extract items in a natural order, then hash tables are your best choice because they offer constant time insertion, search, and deletion. On the other hand, if memory is tight, you do not know how many items you may need to store in memory, and/or you need to be able to extract objects in a natural order, then a tree is a better choice.

Another condition you might want to consider when making your decision is the balance of operations that will be performed on your collection. For example, you may not know how many items you need to store in your collection (so you wouldn’t know how to best size a hash table), but you know that data will be loaded and inserted into your collection on startup and then all future operations will be searches. In this situation, you might be willing to accept rehashing your table (possibly multiple times) during startup to gain constant time search. On the other hand, if items will be consistently added and removed and you do not know how many items will be stored in your collection, then you might be willing to accept O(log n) search time to avoid potentially rehashing a table at runtime.

The point is that there is no general correct answer to whether a hash table or a tree is better, the nature of the data and the nature of the operations you will be performing on that data will determine the correct solution. The key is for you to understand how both solutions work and the benefits and tradeoffs of both solutions so that given the constraints of the problem, you are equipped to make the best decision.