Scipy 课后练习

Exercise 10.1: Least squares

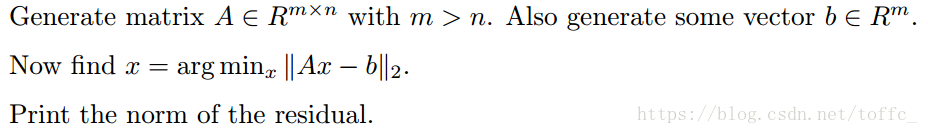
import numpy as np

A = np.random.normal(size=(5,3))
b = np.random.normal(size=(5,1))
x = np.dot(np.dot(np.linalg.inv(np.dot(A.T, A)), A.T), b)

print("x:")
print(x)

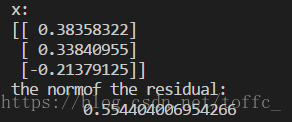
print("the normof the residual: \n\t", end='')
print(np.linalg.norm(x))

result：

Exercise 10.2: Optimization

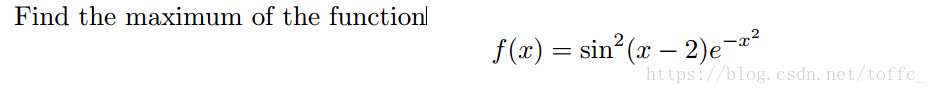
import numpy as np 
import scipy.optimize as opt

def m(x):
    return -np.sin((x - 2) * np.exp(-x**2))**2

maximum = opt.minimize(m, 0)['x'][0]
print("The maximum is " + str(maximum))

Exercise 10.3: Pairwise distances

import numpy as np 
import scipy.spatial as spt 

X = np.random.randint(0, 100, (10, 5))
print(X)
print(spt.distance.pdist(X))

[[50 20 92  6 92]
 [90  9  5 47 63]
 [11 56 46 99 10]
 [95  8 13 53 14]
 [95 24 98 55 66]
 [49 52 11 75 31]
 [85 73 75 22 70]
 [23 71 51 24 92]
 [ 9 31 80 95 56]
 [98 67 61 44 72]]
[108.68302535 142.4991228  129.24008666  71.79136438 126.75961502
  71.15476091  73.04108433 105.65509926  85.54530963 125.07597691
  50.26927491  94.72064189  73.30757123  98.46319109 108.71522432
 122.56834828  81.57205404 112.16505695 125.92060991  60.84406298
 127.02361985 112.88489713  62.58594091 121.58947323 100.94057658
  69.49100661 110.75197515 132.37069162 126.26163313  96.11971702
 109.97272389  64.30396566 106.01415     97.30878686  58.17215829
 100.81170567  94.65199417  88.47033401  88.13625815  70.08566187
 114.41153788  29.81610303  94.73119866  80.87644898 111.51233116]