ProblemSet of Union Find

最新推荐文章于 2025-05-08 10:41:00 发布
原创 最新推荐文章于 2025-05-08 10:41:00 发布 · 253 阅读 · 0 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

本文深入探讨了并查集的基本概念及其多种实现方式，包括快速查找、快速合并、加权快速合并以及加权路径压缩等，并通过具体示例展示了如何应用这些算法解决实际问题。

并查集模板：

快速查找 并查集

这是一个eager的并查集，就是在合并两个节点的时候将这两个节点的组份id修改成同一个根节点的编号.

public class QuickFindUF {

	private int[] componentID; //各个节点（数组索引）所属的组份（数组值）
	private int count; // number of components

	public QuickFindUF(int n)
	{
		if(n<0) throw new IllegalArgumentException();
		this.count=n;
		this.componentID=new int[n];
		for(int i=0;i<n;i++)
		{
			componentID[i]=i;
		}
	}
	
	//连接两个节点    O(n)
	public void union(int p,int q){
		int rootP=this.find(p);
		int rootQ=this.find(q);
		if(rootP==rootQ)
			return;
		int label=Math.min(rootP, rootQ);
		int max=Math.max(rootP, rootQ);
		for(int i=0;i<this.componentID.length;i++)
			if(this.componentID[i]==max)
				this.componentID[i]=label;
		count--;
	}
	
	//在查找p节点所属组份ID过程中会将实际上同属于一个组份的不同ID修改成相同
	public int find(int p)
	{
		int n=this.componentID.length;
		if(p<0||p>=n)
			throw new IllegalArgumentException("index " + p + " is not between 0 and " + (n-1));
		while(p!=this.componentID[p])
		{
			this.componentID[p]=componentID[componentID[p]];
			p=componentID[p];
		}
		return p;
	}
	
	public boolean isConnected(int p,int q)
	{
		int n=this.componentID.length;
		if(p<0 || p>=n || q<0 || q>=n)
			throw new IllegalArgumentException("index " + p +" or "+q+ " is not between 0 and " + (n-1));
		return this.find(p)==this.find(q);
	}

	public int count()
	{
		return this.count;
	}
}

快速合并 并查集

public class QuickUnionUF {

	private int[] componentID;
	private int count; // number of components
	
	public QuickUnionUF(int n)
	{
		if(n<0) throw new IllegalArgumentException();
		this.count=n;
		this.componentID=new int[n];
		for(int i=0;i<n;i++)
		{
			componentID[i]=i;
		}
	}

	//连接两个节点
	void union(int p,int q)	//O(N)
	{
		int rootP=this.find(p);
		int rootQ=this.find(q);
		if(rootP==rootQ)
			return;
		this.componentID[rootP]=rootQ;
		count--;
	}
	
	//在查找p节点所属组份ID过程中会将实际上同属于一个组份的不同ID修改成相同
	int find(int p)	//O(N)
	{
		int n=this.componentID.length;
		if(p<0||p>=n)
			throw new IllegalArgumentException("index " + p + " is not between 0 and " + (n-1));
		while(p!=this.componentID[p])
		{
			this.componentID[p]=componentID[componentID[p]];
			p=componentID[p];
		}
		return p;
	}
	
	boolean isConnected(int p,int q)	//O(N)
	{
		int n=this.componentID.length;
		if(p<0 || p>=n || q<0 || q>=n)
			throw new IllegalArgumentException("index " + p +" or "+q+ " is not between 0 and " + (n-1));
		return this.find(p)==this.find(q);
	}

	int count()
	{
		return this.count;
	}

加权快速合并 并查集

public class WeightedQuickUnionUF {

	/*
	 * 加权快速合并并查集在快速合并并查集基础上：把 深度较小的树合并到较大的树上
	 */
	int[] componentID;
	int[] size; //以下标i为根节点的节点数
	int count; // number of components
	
	
	
	public WeightedQuickUnionUF(int n)  //O(N)
	{
		if(n<0) throw new IllegalArgumentException();
		this.count=n;
		this.componentID=new int[n];
		this.size=new int[n]; //以索引i为根节点的树的总结点数
		
		for(int i=0;i<n;i++)
		{
			componentID[i]=i;
			this.size[i]=1;
		}
	}
	
	//连接两个节点
	void union(int p,int q)	//O(1)
	{
		int rootP=this.find(p);
		int rootQ=this.find(q);
		if(rootP==rootQ)
			return;
		if(this.size[rootP]<=this.size[rootQ])
		{
			this.size[rootQ]+=this.size[rootP];
			this.componentID[rootP]=rootQ;
		}
		else
		{
			this.size[rootP]+=this.size[rootQ];
			this.componentID[rootQ]=rootP;
		}
		count--;
	}
	

	//在查找p节点所属组份ID过程中会将实际上同属于一个组份的不同ID修改成相同
	int find(int p)  //O(N),O(the depth of p) if given root nodes
	{
		int n=this.componentID.length;
		if(p<0||p>=n)
			throw new IllegalArgumentException("index " + p + " is not between 0 and " + (n-1));
		while(p!=this.componentID[p])
		{
			this.componentID[p]=componentID[componentID[p]];
			p=componentID[p];
		}
		return p;
	}
	
	boolean isConnected(int p,int q)
	{
		int n=this.componentID.length;
		if(p<0 || p>=n || q<0 || q>=n)
			throw new IllegalArgumentException("index " + p +" or "+q+ " is not between 0 and " + (n-1));
		return this.find(p)==this.find(q);
	}

	int count()
	{
		return this.count;
	}
}

加权路径压缩快速合并 并查集

public class WeightedQuickUnionPathCompressionUF {

    int[] father;
    int[] size;
    int count; // number of components

    public WeightedQuickUnionPathCompressionUF(int n)  //O(N)
    {
        if(n<0) throw new IllegalArgumentException();
        this.count=n;
        this.father=new int[n];
        this.size=new int[n]; //以索引i为根节点的树的总结点数

        for(int i=0;i<n;i++)
        {
            father[i]=i;
            this.size[i]=1;
        }
    }

    //连接两个节点
    boolean union(int p,int q)	//O(1)
    {
        int rootP=this.find(p);
        int rootQ=this.find(q);
        if(rootP==rootQ)
            return false;
        if(this.size[rootP]<=this.size[rootQ])
        {
            this.size[rootQ]+=this.size[rootP];
            this.father[rootP]=rootQ;
        }
        else
        {
            this.size[rootP]+=this.size[rootQ];
            this.father[rootQ]=rootP;
        }
        count--;
        return true;
    }

    //在查找p节点所属组份ID过程中会将实际上同属于一个组份的不同ID修改成相同
    int find(int p)  //O(N),O(the depth of p) if given root nodes
    {
        int n=this.father.length;
        if(p<0||p>=n)
            throw new IllegalArgumentException("index " + p + " is not between 0 and " + (n-1));

        int root=p;
        while(root!=this.father[root])
            root=this.father[root];
        while(p!=root)
        {
            int new_root=this.father[p];
            this.father[p]=root;
            p=new_root;
        }
        return p;
    }

    boolean isConnected(int p,int q)
    {
        int n=this.father.length;
        if(p<0 || p>=n || q<0 || q>=n)
            throw new IllegalArgumentException("index " + p +" or "+q+ " is not between 0 and " + (n-1));
        return this.find(p)==this.find(q);
    }

    int count()
    {
        return this.count;
    }

684. Redundant Connection

class Solution {
    
    public static int maxCount=1010;
    
    public int[] findRedundantConnection(int[][] edges) {
        
        WeightedQuickUnionPathCompressionUF uf=new WeightedQuickUnionPathCompressionUF(maxCount);
        for(int[] e:edges){
            if(!uf.union(e[0],e[1]))
                return e;
            
        }
        return new int[]{0,0};
    }
}

public class WeightedQuickUnionPathCompressionUF {

    int[] father;
    int[] size;
    int count; // number of components

    public WeightedQuickUnionPathCompressionUF(int n)  //O(N)
    {
        if(n<0) throw new IllegalArgumentException();
        this.count=n;
        this.father=new int[n];
        this.size=new int[n]; //以索引i为根节点的树的总结点数

        for(int i=0;i<n;i++)
        {
            father[i]=i;
            this.size[i]=1;
        }
    }

    //连接两个节点
    boolean union(int p,int q)	//O(1)
    {
        int rootP=this.find(p);
        int rootQ=this.find(q);
        if(rootP==rootQ)
            return false;
        if(this.size[rootP]<=this.size[rootQ])
        {
            this.size[rootQ]+=this.size[rootP];
            this.father[rootP]=rootQ;
        }
        else
        {
            this.size[rootP]+=this.size[rootQ];
            this.father[rootQ]=rootP;
        }
        count--;
        return true;
    }

    //在查找p节点所属组份ID过程中会将实际上同属于一个组份的不同ID修改成相同
    int find(int p)  //O(N),O(the depth of p) if given root nodes
    {
        int n=this.father.length;
        if(p<0||p>=n)
            throw new IllegalArgumentException("index " + p + " is not between 0 and " + (n-1));

        int root=p;
        while(root!=this.father[root])
            root=this.father[root];
        while(p!=root)
        {
            int new_root=this.father[p];
            this.father[p]=root;
            p=new_root;
        }
        return p;
    }

    boolean isConnected(int p,int q)
    {
        int n=this.father.length;
        if(p<0 || p>=n || q<0 || q>=n)
            throw new IllegalArgumentException("index " + p +" or "+q+ " is not between 0 and " + (n-1));
        return this.find(p)==this.find(q);
    }

    int count()
    {
        return this.count;
    }
}

[外交]
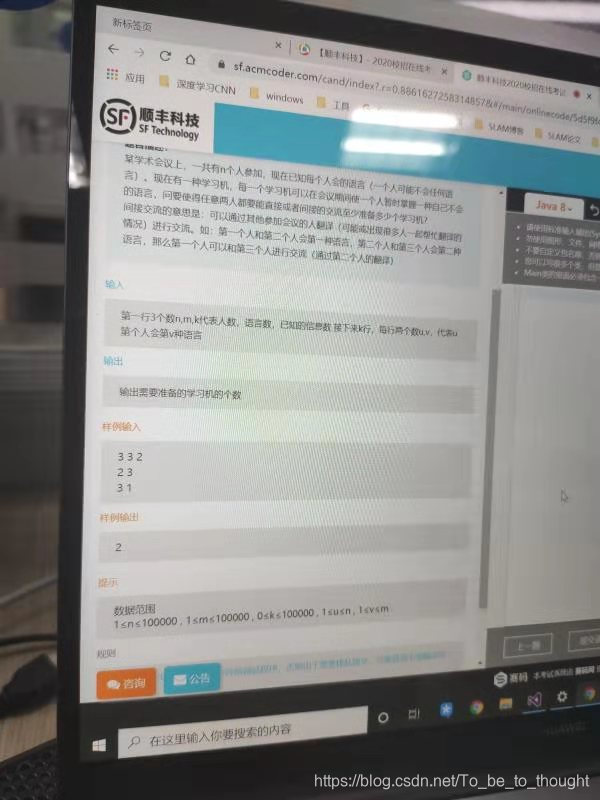
在这里插入图片描述

package ShunFeng;

import java.util.ArrayList;
import java.util.HashMap;
import java.util.Scanner;

public class Main1 {


    public static void main(String[] args) {

        Scanner cin = new Scanner(System.in);

        int n = cin.nextInt();    // 参会人数
        int m = cin.nextInt();    // 语言数量
        int k = cin.nextInt();    // 记录条数
        HashMap<Integer, ArrayList<Integer>> record = new HashMap<>();
        for (int i = 0; i < k; i++) {
            int a = cin.nextInt(), b = cin.nextInt();
            if (record.containsKey(b)) {
                record.get(b).add(a);
            } else {
                ArrayList<Integer> tmp = new ArrayList<>();
                tmp.add(a);
                record.put(b, tmp);
            }
        }
        QuickUnionUF uf = new QuickUnionUF(n);  //建立大小为n的并查集，不会任何语言的人或者只会一种语言（并且该语言不被其他任何人掌握的）始终独立为一个组份
        for (int i : record.keySet()) {
            ArrayList<Integer> arr = record.get(i);
            int a = arr.get(0);
            for (int j = 1; j < arr.size(); j++) {
                uf.union(a-1, arr.get(j)-1);  //人的编号减一对应数组下标的范围
            }
        }
        System.out.println(uf.count()-1);
        /*
        7 4 9
        1 1
        2 1
        3 1
        4 2
        3 2
        4 3
        5 3
        6 3
        3 4
        1->(1,2,3)
        2->(4,3)
        3->(4,5,6)
        4->(3)


        3 3 2
        2 3
        3 1
         */
    }
}

public class QuickUnionUF {
    private int[] componentID;
    private int count; // number of components
    public QuickUnionUF(int n)
    {
        if(n<0) throw new IllegalArgumentException();
        this.count=n;
        this.componentID=new int[n];
        for(int i=0;i<n;i++)
        {
            componentID[i]=i;
        }
    }
    //连接两个节点
    void union(int p,int q)	//O(N)
    {
        int rootP=this.find(p);
        int rootQ=this.find(q);
        if(rootP==rootQ)
            return;
        this.componentID[rootP]=rootQ;
        count--;
    }
    //在查找p节点所属组份ID过程中会将实际上同属于一个组份的不同ID修改成相同
    int find(int p)	//O(N)
    {
        int n=this.componentID.length;
        if(p<0||p>=n)
            throw new IllegalArgumentException("index " + p + " is not between 0 and " + (n-1));
        while(p!=this.componentID[p])
        {
            this.componentID[p]=componentID[componentID[p]];
            p=componentID[p];
        }
        return p;
    }
    boolean isConnected(int p,int q)	//O(N)
    {
        int n=this.componentID.length;
        if(p<0 || p>=n || q<0 || q>=n)
            throw new IllegalArgumentException("index " + p +" or "+q+ " is not between 0 and " + (n-1));
        return this.find(p)==this.find(q);
    }
    int count()  //返回组份数
    {
        return this.count;
    }
}
Disjoint Set Union
2301_78527293的博客
08-01 429
并查集题目合集，以kuangbin专题为主
普林斯顿大学算法课1算法第四版 Union−Find课程总结quick find, quick union, weighted quick union（with path）
weixin_43854443的博客
03-09 712
序言 本文是我个人对coursera上普林斯顿大学的课程分节总结，主要介绍核心思路和代码实现。课程地址如下： 普林斯顿-算法part1，课程深入浅出，并附有配套书籍和网站，十分适合我这样的入门者学习算法。 写博文的目的有两个方面 由于是课外的学习，需要转化成果来增加自己的动力 输出是最好的复习方式 那么废话不多说，让我们先来看看这一节讲了些什么。 本节简介 本节以从一个物理模型开始抛出动态连接...
图论基础之Union Find
圣·马坡岭皇家码农
08-09 482
Concept Union Find通常被翻译为并查集，让人听起来觉得非常高深莫测，为此，我给它起了个外号 叫做：“认祖宗”！ 没错，寻找根节点的过程难道不就叫“认祖宗”吗？ 我们可以把图论中的一些术语用日常生活用语联系起来： 节点：形形色色的人 边：父子关系 根：一群人的祖宗 并查集就是把一群人用一种算法分成不同家族。 其中一个重要的过程就是认亲。 所以，并查集有如下几个要素...
数据结构之并查集 Union Find 剖析
chen
03-15 703
数据结构之并查集 Union Find 剖析 文章目录数据结构之并查集 Union Find 剖析概述原理时间复杂度分析实现实现Quick Find并查集实现Quick Union并查集考虑size优化并查集基于rank优化并查集路径压缩优化并查集Leetcode 547. Friend Circles相关链接公众号参考 概述 并查集（英文：Disjoint-set data structure，直译为不交集数据结构）： 是一种数据结构， 用于处理一些不交集（Disjoint sets，一系列没有重复元素
Problem Set 4
dingxingdi的博客
03-30 574
处理完所有等于约束之后，再依次检查每个不等于约束是否成立(不等号两边的元素如果在同一集合中就不成立)，如果都成立那么就可以同时满足，否则就不行。.根据数学归纳，两棵子树都是满二叉树，而且两棵子树的大小是相同的，所以两个子树一模一样，在加上根节点可知，整棵树是一个满二叉树，当然也就平衡了。是不是峰值，如果是的话就找到了，如果都不是的话就说明数列在开头一段处于单调递增的状态，末尾一段处于单调递减的状态，于是可以知道在。的时候，设根节点的两个儿子的大小分别为。的数删掉，同时记录删除的数的个数，设为。
Problem Set 6
dingxingdi的博客
05-08 735
我们考虑一个朴素的做法：遍历所有非树边，将每条非树边加入到树中，暴力标记形成的环上与非树边权重相同的树边；由于这条树边不是桥边，所以一定存在连接这两个连通块的边，而且这些边是非树边，我们在前面的循环过程中可以遍历到，而这条树边既然没有被打上标记，就说明这些非树边的权重都严格大于这条树边，而去掉这条树边之后。要判断一条树边是不是临界边，就是要判断是否存在一条与其权重相同的非树边，使得加入这条非树边形成的环上包含这条树边。之后，剩余的树不是剩余子图的MST，那么我们将这颗剩余的树换成MST，再加上。
Problem Set 2
dingxingdi的博客
03-11 934
Problem Set 2.1 Problem 2.1.1 将\(2n\)个人按照评分从大到小排序，前\(n\)个人为一组，后\(n\)个人为一组，根据贪心不难知道算法正确 def max_score_difference(scores, n): scores.sort(reverse=True) sum_team1 = sum(scores[:n]) sum_team2...
Leetcode: Number of Islands II && Summary of Union Find
weixin_30360497的博客
12-30 120
A 2d grid map of m rows and n columns is initially filled with water. We may perform an addLand operation which turns the water at position (row, col) into a land. Given a list of positions to ...
并查集 Union Find
底层码农
11-06 6458
并查集 Union Find
Almost Union-Find
smoggyxhdz的博客
07-21 349
并查集的删除操作，可以看做是类似树的懒惰删除， 废弃该节点，但不删除，用根结点记录这个并查集的容量和大小，在节点被废弃后，从它的根节点处删除这个节点的数据 用一个新的节点替换该节点获得其的属性，代替它加入到新的并查集中 可以用一个id[i]数组代替i Almost Union-Find Time Limit: 1000MS   Memory Limit: Unkn
基础数据结构和算法一：UnionFind
George's dev dream port
11-19 180
  The problem that we consider is not a toy problem; it is a fundamental computational task, and the solution that we develop is of use in a variety of applications, from percolation in physical ch...
cf2146B.Merging the Sets https://codeforces.com/problemset/problem/2146/B
最新发布
10-10
题目标签或常见解法：在Codeforces上，"Merging the Sets" 可能是一个关于集合合并、并查集(Union-Find)或类似算法的问题。2146B是题目编号，我需要确认。 用户提到了链接，所以我应该假设这是一个真实题目。从记忆...
union find 算法 可用在聚类
tattarrattat的专栏
07-02 1590
 并查集(Union-Find Sets)2009-02-23 12:38本文通过几道题介绍一下并查集的应用。 第一道题目：The Suspects (http://acm.pku.edu.cn/JudgeOnline/problem?id=1611)1. N个人编号,从0到N-1。2. 给出这N个人分成M个集合的描述(同一个人可以加入不同
【PTA】【数据结构与算法】并查集
葑鈊丶
01-10 7010
选择题 1.The array representation of a disjoint set containing numbers 0 to 8 is given by { 1, -4, 1, 1, -3, 4, 4, 8, -2 }. Then to union the two sets which contain 6 and 8 (with union-by-size), the inde...
模拟退火算法（附python代码）
热门推荐
To_be_thinking的博客
08-21 1万+
https://www.cnblogs.com/ranjiewen/p/6084052.html这篇文章把模拟退火的来龙去脉讲得十分清楚，下面直接上代码。值得注意的是对于不同的问题，其中的关键一步随机扰动的选择是不一样的，如果选择不当会导致搜索域变小或者很难达到最优解（较优），并且求得的解不一定就是最优解。 Q1：第一个例子就是求一个一元函数y=x+10sin(5x)+7cos(4x)的最小值：...
高斯混合模型（GMM）源代码实现（二）
To_be_thinking的博客
06-03 5586
第一篇(https://blog.youkuaiyun.com/To_be_to_thought/article/details/90759715)讲了原理推导，网上有很多讲解原理的很少有实现的。Talk is cheap,show the code. 第二篇主要是GMM的实现，先用面向过程的方式实现并检验算法的正确性，再用面向对象的方式进行封装。然后再对比sklearn的源代码库进行分析比较。 算法流程...
感知机算法（Perceptron Learning Algorithm）和代码实现（Python）
To_be_thinking的博客
09-18 4550
PLA算法是机器学习中最为基础的算法，与SVM和Neural Network有着紧密的关系。                                                                                                  import numpy as np import matplotlib.pyplot as p...
优化梯度下降算法 Momentum、RMSProp(Root mean square propagation)和Adam( Adaptive Moment Estimation)
To_be_thinking的博客
09-26 3044
https://blog.youkuaiyun.com/To_be_to_thought/article/details/81780397阐释Batch Gradient Descent、Stochastic Gradient Descent、MiniBatch Gradient Descent具体原理。 对于梯度下降算法，当参数特别多时容易发现，速度会变慢，需要迭代的次数更多。优化速度与学习率、梯度变化量...
迷宫问题的递归和非递归解法
To_be_thinking的博客
05-05 2854
迷宫问题一般可以建模为一个二维数组，二维数组的值表示位置（i，j）是否可以通行,将位置数据结构设为 每个格网的数据结构 public class Loc { int row_idx; int col_idx; Loc pre; boolean pass; boolean visited; public Loc(int i,int j,Loc pre,boolean pass,...
评论
成就一亿技术人!
拼手气红包6.0元
还能输入1000个字符
 
红包 添加红包
表情包 插入表情
表情包 代码片
 条评论被折叠 查看
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值