【23-24 秋学期】NNDL 作业8 卷积 导数 反向传播

习题5-2 证明宽卷积具有交换性， 即公式(5.13)．

习题5-4 对于一个输入为100 × 100 × 256的特征映射组， 使用3 × 3的卷积核， 输
出为100 × 100 × 256的特征映射组的卷积层， 求其时间和空间复杂度． 如果引入
一个1 × 1卷积核， 先得到100 × 100 × 64的特征映射， 再进行3 × 3的卷积， 得到
100 × 100 × 256的特征映射组， 求其时间和空间复杂度．

习题5-5 对于一个二维卷积， 输入为3 × 3， 卷积核大小为2 × 2， 试将卷积操作重
写为仿射变换的形式． 参见公式(5.45) .

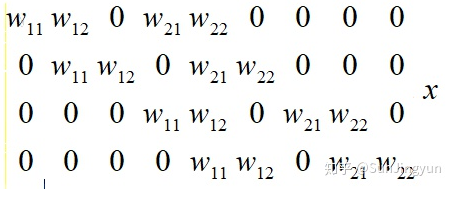
附加题 阅读 “5.3.1 卷积神经网络的反向传播算法”，举例说明推导过程.

在卷积神经网络 (Convolutional Neural Network, CNN) 中，反向传播算法用于更新网络的权重和偏置。下面是推导过程的示例，其中我们假设有一个包含两个卷积层和一个全连接层的简单CNN。

首先，我们定义损失函数，通常使用交叉熵损失函数。然后，我们使用反向传播算法计算每个参数的梯度，并使用梯度下降法来更新参数。 假设我们的CNN网络结构如下：

1. 输入层：输入图像的像素值
2. 卷积层1：包含多个卷积核（filter）和对应的偏置项（bias）
3. 激活层1：使用ReLU激活函数 池化层1：使用最大池化操作
4. 卷积层2：包含多个卷积核和偏置项
5. 激活层2：使用ReLU激活函数
6. 池化层2：使用最大池化操作
7. 全连接层：将特征图展平为一维向量，并连接到输出层
8. 输出层：使用softmax激活函数输出类别概率

假设我们要训练这个CNN来进行图像分类任务，现在我们来看看如何使用反向传播算法来更新卷积层1的权重和偏置项。

前向传播：首先，我们将输入图像通过卷积层1，激活层1和池化层1，得到特征图。具体操作包括：使用卷积核对输入图像进行卷积操作，加上偏置项，然后通过ReLU激活函数进行激活，最后使用最大池化操作来降低特征图的尺寸。假设卷积层1的输出特征图为A。

反向传播：

• a. 计算输出层的误差：使用损失函数计算输出层的误差。
• b. 计算全连接层的误差：将输出层的误差通过权重矩阵传播到全连接层，得到全连接层的误差。
• c. 计算池化层2的误差：将全连接层的误差通过全连接层的权重矩阵传播到池化层2，得到池化层2的误差。
• d. 反向传播到卷积层2：将池化层2的误差通过池化操作传播到卷积层2，得到卷积层2的误差。
• e. 反向传播到激活层1：将卷积层2的误差通过激活函数的导数传播到激活层1，得到激活层1的误差。
• f. 反向传播到卷积层1：将激活层1的误差通过卷积操作传播到卷积层1，得到卷积层1的误差。

更新参数：根据卷积层1的误差，计算卷积核和偏置项的梯度。具体操作包括：计算卷积核的梯度，即将卷积层1的误差与输入图像进行卷积操作；计算偏置项的梯度，即卷积层1的误差的元素和。然后，使用梯度下降法更新卷积核和偏置项的值。

习题 5-7 忽略激活函数， 分析卷积网络中卷积层的前向计算和反向传播（公式
(5.39)） 是一种转置关系．

习题5-8 在空洞卷积中， 当卷积核大小为𝐾， 膨胀率为𝐷时， 如何设置零填充𝑃 的
值以使得卷积为等宽卷积 .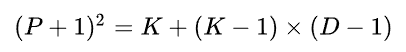

其中，P表示零填充的数量。通过计算得到的P值，可以确定需要在输入特征图的周围填充多少个零值，以便在应用空洞卷积时，输出特征图的宽度与输入特征图的宽度保持一致，从而实现等宽卷积。