蓝桥杯---子串分值（数学）

子串分值

题目描述
对于一个字符串 SS，我们定义 SS 的分值 f(S)f(S) 为 SS 中恰好出现一次的字符个数。例如 f(“aba”) = 1，f(“abc”) = 3, f(“aaa”) = 0f(“aba”)=1，f(“abc”)=3,f(“aaa”)=0。

现在给定一个字符串 S0⋯n−1，（长度为 n，1≤n≤10^5
），请你计算对于所有 SS 的非空子串 Si…j(0 ≤ i ≤ j < n)(0≤i≤j<n),f(S i⋯j) 的和是多少。

输入描述
输入一行包含一个由小写字母组成的字符串 SS。

输出描述
输出一个整数表示答案。

输入

ababc

输出

21

运行限制
最大运行时间：1s
最大运行内存: 256M
思路1：

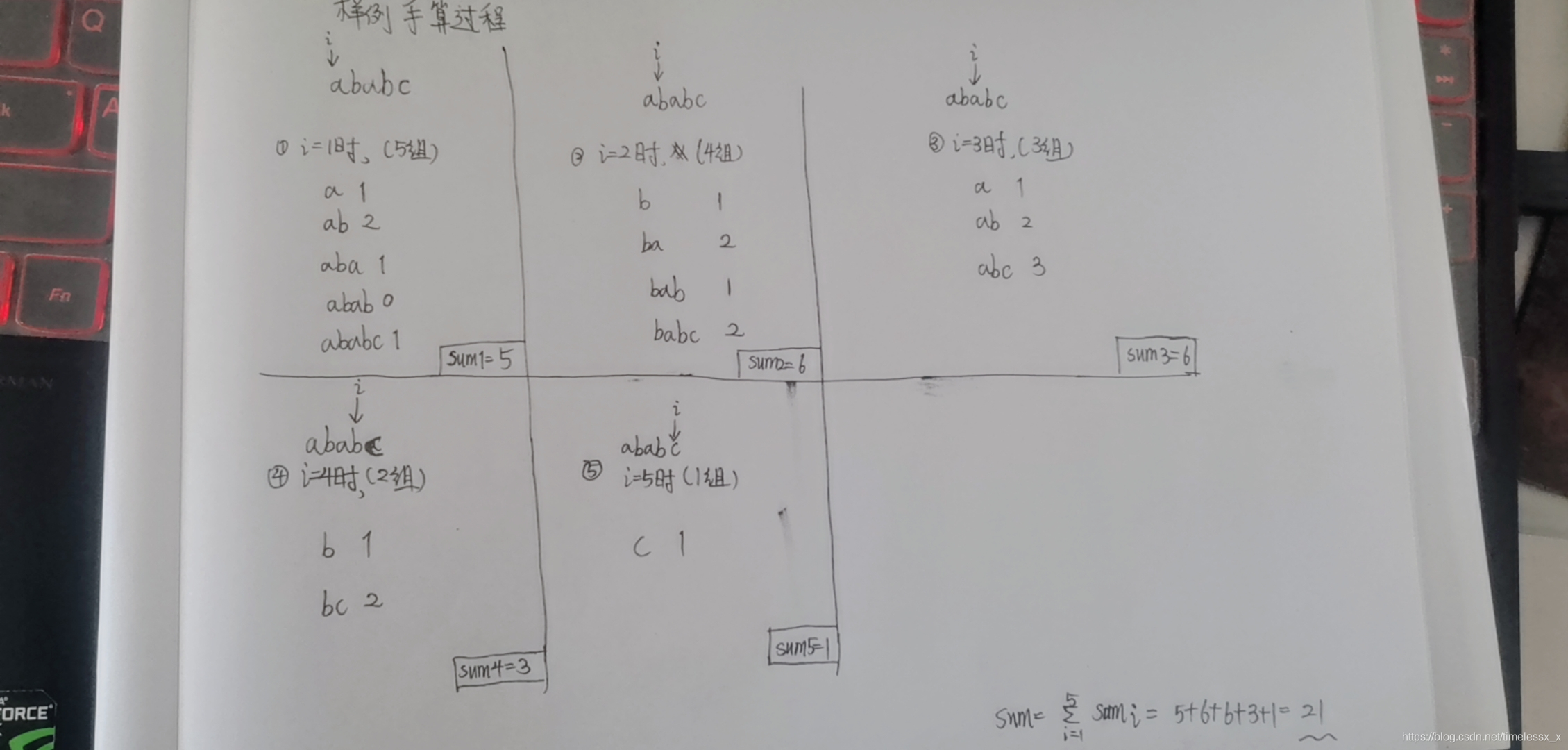
所以外层循环i为起始位置控制；
内层j从i到n，且没有重复的score++，且ans+=score；
有一个重复的（即vis[j]==1时）score–，且ans+=score；
code:（60%）

#include<stdio.h>
#include<iostream>
#include<cstring>

using namespace std;
char s[100003];
int vis[27];
int main()
{
    scanf("%s",s);
    int len=strlen(s);
    int sum=0;
    for(int i=0;i<len;i++){
        memset(vis,0,sizeof vis);
        int score=0;
        for(int j=i;j<len;j++){
            if(vis[s[j]-'a']==0){
                score++;
                sum+=score;
                vis[s[j]-'a']++;
            }else{
                if(score>=1&&vis[s[j]-'a']==1){
                    vis[s[j]-'a']++;
                    score--;
                }
                sum+=score;
            }
        }
    }
    printf("%d",sum);
    return 0;
}

思路2：
对于每一个字符求其对sum的贡献值；
仔细观察会发现：每个字符的贡献值=（当前下边index-前一个相同字符下标）*（下一个相同字符下标-当前下标index）
如果前面没有相同的字符，就默认前一个相同字符下标为0；
如果后面没有相同的字符，就默认后一个相同字符下标为s_length;

把所有的字符贡献值累加在一起即可！
accept code：

#include<iostream>
#include<string.h>
#include<string>

using namespace std;
#define   MAX   100003
int main()
{
    string s;
    int pre[MAX],next[MAX],a[27];
    cin>>s;
    s="0"+s;
    int len=s.length();
    for(int i=0;i<27;i++){
        a[i]=0;
    }

    for(int i=1;i<len;i++){
        int index=s[i]-'a';
        pre[i]=a[index];
        a[index]=i;
    }

    for(int i=0;i<27;i++){
        a[i]=len;
    }

    for(int i=len-1;i>=1;i--){
        int index=s[i]-'a';
        next[i]=a[index];
        a[index]=i;
    }
    long long int ans=0;
    for(int i=1;i<len;i++){
        ans+=(long long)((i-pre[i])*(next[i]-i));
    }
    printf("%lld",ans);
    return 0;
}