FP-growth算法来高效发现频繁集_fpgrowth算法算频繁项集-优快云博客

本文详细介绍了FP-growth算法，一种用于高效发现频繁集的算法，对比Apriori算法，FP-growth只需对数据扫描两次。文章分为FP树介绍、FP树构建和从FP树挖掘频繁项集三个部分，通过实例解析算法流程，包括如何构建FP树和从FP树中抽取频繁项集。通过对数据的排序和筛选，构建FP树并利用条件模式基构建条件FP树，从而迭代地发现频繁集。

FP-growth算法是一种高效发现频繁集的算法，比Apriori算法高效，但是不能用于发现关联规则。FP-growth算法只需要对数据即信两次扫描，而Apriori算法对于每个潜在的频繁项集都会扫描数据集判定给定模式是否是频繁，所以FP-growth更快。FP-growth算法主要分为两个过程：

构建FP树；
从FP树中挖掘频繁项集。

1.FP树介绍

FP代表频繁模式（Frequent Pattern）,它和数据结构中的其它树特别相似，但是在FP树中，一个元素项可以出现多次，如下图所示：

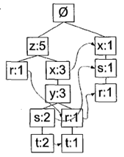
图1

如图1所示，FP树会存储项集的出现频率，而每个项集会以路径的方式存储在树中。从最上面的空集合开始，每一条路径就是一个项集，这里要除过去带箭头的那些路径链接，因为带箭头的的链接是相似项之间的链接，叫节点链接，是用于快速发现相似项的位置（至于相似项是什么，看后面就知道其含义了）。

这棵树可以分为纵向和横向的，纵向的就是每个项集的集合，横向的就是相似项，用于方便元素的查找。

为了挖掘频繁项集，我们首先要构建FP树。我们需要对数据扫描两遍。第一遍对所有元素项的出现次数进行统计，根据Apriori原理，如果某元素不是频繁的，那么包含该元素的超集也是不频繁的，所以就不需要考虑这些超集，第二遍扫描值考虑哪些频繁元素。

2.构建FP树

首先给出FP树的节点的结构：

class treeNode:
    def __init__(self, nameValue, numOccur, parentNode):
        self.name = nameValue
        self.count = numOccur
        self.nodeLink = None
        self.parent = parentNode      #needs to be updated
        self.children = {}

    def inc(self, numOccur):
        self.count += numOccur

    def disp(self, ind=1):
        print ' '*ind, self.name, ' ', self.count
      &nb