隐马尔科夫模型

1.隐马尔科夫模型介绍

        隐马尔可夫模型是关于时序的概率模型，描述有一个隐藏的马尔科夫链随机生成不可观测的随机序列，在有各个状态生成一个观测而产生观测序列的过程。

                               

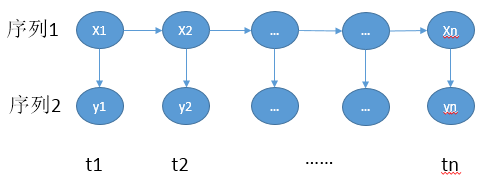
                                                                                     图1

        隐马尔可夫模型可以简单的表示为图1所示的模型。序列1是随机生成的不可观测的隐序列，也成为状态序列；中在每一个t时刻，隐序列的每个状态xn可以生成对应的状态yn，所有的yn组成了序列2，是我们可以实际观测到的序列，称为观测序列。

        设Q是所有可能的状态序列，V是所有可能的观测序列，表示形式如下：

                                              

        N就表示所有的状态数，M就表示所有的观测数。

        序列1可以表示为：I=(i1,i2,⋯,iT)，表示为长度为T的状态序列；序列2可以表示为，表示为状态序列对应的观测序列。

        对于时序的概念，肯定要有从一个时刻到下一时刻的改变，也就是状态转移；马尔可夫模型中只有隐状态的转移，状态集合为Q，一共有N个状态，所以可以将所有的状态转移情况表示为一个N×N的矩阵形式：

                                                        

其中

                                                    

        表示t时刻状态为qi，到t+1(下一时刻)，状态为qj的概率。

        每一时刻的状态都会生成一个观测值，所以观测值是通过状态来确定的，而观测值之间没有必然的联系，那么我们就需要给出各个状态生成各个观测值的概率，状态有N个，观测值有M个，所有我们可以表示为一个N×M的矩阵：