理解Logistic回归：从分布到分类-优快云博客

本文链接：https://blog.youkuaiyun.com/things_use/article/details/102455621

Logistic回归是一种分类算法，不同于预测算法。它使用Logistic分布和sigmoid函数处理二分类问题，与线性回归有密切关系。Logistic模型的条件概率分布通过极大似然估计方法求解参数，优化过程可以采用梯度上升法或其变种，如随机梯度上升法和小批量梯度法。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

“回归”一词，第一印象指的是线性回归，是一种预测算法；而Logistic回归算法中虽然也有“回归”，但是他并不是预测算法，而是一种分类算法，用于二分类的问题，但是它和线性回归还是有一定的关系的。

Logistic分布

首先我们给出Logistic分布函数如下：

其中μ是函数位置，γ>0为形状参数。我们取μ=0，γ=1得到下面分布函数(x用z代替)：

画出上面函数的图像如下：

这里可以看到，上述函数图像中函数的上限是无限接近于1，函数的下限是无限接近于0，而F(0)=0.5，即函数图像以（0,0.5）形成中心对称。这个函数是单调递增的。

对于二分类算法，我们常用的是0和1进行标记，0表示正例，1表示反例，具有明显的不连续性即

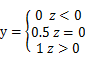
所以我们可以看到这个函数是非连续的函数，在具体的算法中比较难以进行计算，所以我们需要一个连续的函数，所以sigmoid函数就可以很好的解决这个问题，可以代替非连续的单位阶跃函数，并且是连续可微的，图像如上图所示。

线性回归和Logistic回归的关系

设中，为了计算方便，将权值向量和输入向量加以扩充，仍记作ω和x,即ω={ω1,ω2,…ωn,b},x={x1,x2,…xn,1 }将其带入sigmoid函数中我们得到

即

因为logistic多用于二分类算法，0反例，1是正例，所以我们这里定义二项Logistic回归模型的条件概率分布：

设正例发生的概率是p，则反例发生的概率是1-p，将上面两个式子相比我们得到：

即，我们得到左边是一个对数，右面就是我们熟悉的线性回归函数，其中p比上1-p即事件发生的概率比上事件不发生的概率指的是一个事件的几率，而几率的对数就是我们熟悉的线性回归函数。所以输出Y=1的对数几率是由输入x的线性函数表示的模型，即logistic模型。

模型参数估计

上面已经介绍了logistic模型，接下来就是正经的学习过程了，也就是求ω和b的过程了。

由于这个是二分类模型，即,所以满足0-1分布模型。我们可以用极大似然估计方法进行参数估计，从而得到Logistic模型。

令P(Y=1|x)=h(x) , P(Y=0|x) = 1-h(x)得到似然函数：

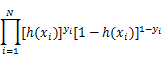
对其求对数，将乘法运算转化为对数的加法运算，得到其对数似然函数为：

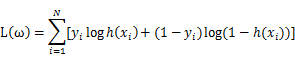
带入相关表达式的

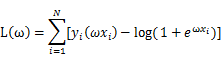
我们的目标就是最大化似然函数，然后我们对L(ω)中的ω求导得:

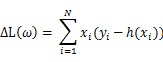
所以可以得到ω的迭代公式，，其中α是学习率，需要我们指定。到此为止，就可以得到了参数的迭代公式，我们就可以通过训练数据进行参数估计了。

算法优化

计算上面的参数过程，很明显我们使用的是梯度上升法，从上面的的求梯度的公式，我们可以看到，每次迭代我们都要用到所有的训练数据，这样数据少的话还可以，但是数据多的话就会有很大的计算量，所以我们可以采用随机梯度上升法，即每次迭代的中只选取一组值即令。采用这种算法，虽然计算简单，但是模型的误差也会相对较大。