朴素贝叶斯法

1. 概述

    朴素贝叶斯法是基于贝叶斯定理与特征条件独立假设的分类方法。对于给定的训练数据集，首先基于特征条件独立假设学习输入/输出的联合概率分布；然后基于此模型，对于给定的输入x，利用贝叶斯定理求出后验概率最大的输出y。、

上面的一段话是李航《统计学习方法》中的一段话，中间涉及到了一些基本概念，是贝叶斯方法的前提。

条件独立假设：这是贝叶斯方法的前提条件，

条件概率公式：

P(B|A) = P(AB)/P(A)，这个是条件概率公式，P(AB)是联合概率。

贝叶斯公式：

P(A|B) = (P(B|A)P(A))/P(B)

    贝叶斯公式是通过条件概率推导过来的。上面的条件概率也可以写成P(A|B) = P(AB)/P(B)，从这里我们可以看出，条件A和B是相对的，这里假设A是我们要的分类的结果，B是条件，联合两个条件概率，我们得到上面的贝叶斯公式：在B的情况下，结果是分类A的概率，在这种情况下，我们成P(A)为先验概率，P(A|B)称为后验概率；所以贝叶斯公式就是我们熟悉的由先验概率求后验概率的公式；贝叶斯公式中分子是P(B|A)p(A)，结合上面的条件概率公式，可知分子是联合概率，所以我们要通过先验概率和条件概率先求出联合概率，然后在求其后验概率；而P(A)和P(B|A)都是我们可以通过样本得出来的。贝叶斯的学习过程，也就是通过样本数据计算P(A)和P(B|A)的过程。

    这个分母是什么，简单的看就是：是条件B的概率，在贝叶斯公式中，我们就是要通过条件B来求A，即对应的分类，所以这个结果是变量，B相对是不变的；更通俗的说是在条件B下计算各种分类的概率，所以这个时候对于所有分类，分母是不变的；用公式解释如下，即全概率公式：

，将其带入上面的贝叶斯公式得到更详细的贝叶斯公式：

,即在条件B下，分类结果是Ai的概率。

1. 模型

上面介绍的是贝叶斯方法的基本理论知识，下面就是将其推广到实用的层面。

我们前面也说了贝叶斯方法是建立在条件独立假设之上的，我们这里用X表示条件，Y表示结果（我觉得将X理解为自变量，Y理解为因变量），对于条件X可能是有多个属性组成的，而这些个条件都是相互独立的；即如果判断一个水果是苹果还是梨，我们可以通过颜色和形状判断，那么这个颜色和形状是相互对立互不影响的。所以具体的，条件独立性假设公式为：

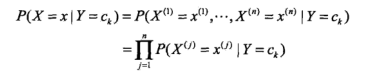
将上面的贝叶斯公式换成自变量X和因变量Y,

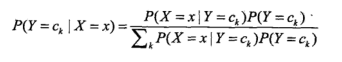
然后再讲独立性假设公式带入贝叶斯公式：

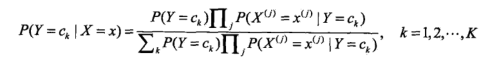
这个就是我们最终得到的计算公式。通过概述中，我们可以知道，对于所有的分类分母都是相同的，所以我么只计算分子部分就可以了。所以最终的分类器如下

arg表示取概率最大的那个分类。

1. 极大似然估计、学习分类算法

这里的估计是用频率代替概率，所以先验概率P(Y=)，的极大似然估计是：

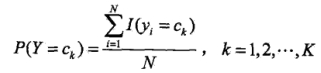
分子是所有分类为ck的数量，N是所有样本的数量。

 

在多特征的样本里，每个x有多个特征（形状和颜色），而每个特征又有多个取值（如颜色：红色、白色、灰色，青色。。。。）。设第j个特征可能取值的集合为{，，…，，}，条件概率P(=|Y=)的极大似然估计是：

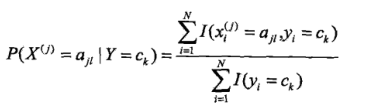
分子是分类结果是ck的总数，分子式分类结果是ck中特征值是的个数。

学习分类算法的过程就是计算所有特征的所有取值的条件概率，以及所有的先验概率，最后对于需要分类的样本（给定的测试数据），计算：

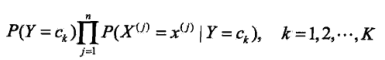
比较结果最大的那个分类，就是我们估计的测试样本的分类。

1. 贝叶斯估计

贝叶斯方法存在一个缺陷：如果如果某个分类下，某个特征的某个取值，对应的样本数量是0，那么它对应的条件概率就是0，那么最后进行分类的时候，概率就成了0,这样明显是不合适的，就会使分类出现偏差，所以为了解决这个偏差，采用贝叶斯估计,具体条件概率的贝叶斯估计是：

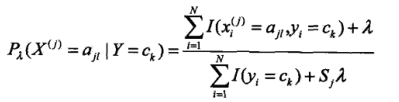
我们可以看到是在贝叶斯方法的条件概率的分子分母上都加上了常数项，其中λ>=0，当λ时0的时候，就回归成了我们前面说的极大似然估计了。取λ=1,成为拉普拉斯平滑（拉普拉斯修正）。

所以，对于所有的条件概率都有：

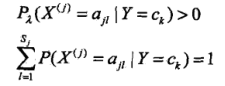
其中的是每个特征中，特征值的个数。

同理先验概率的贝叶斯估计如下：

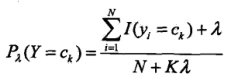
K是分类种类数，N是样本总数。

 

最后，这里只是结合李航的《统计学习方法》，自己做了一些总结和自己的理解，只是做了理论的推导，具体还要结合实际应用才能更加深入一步了解啊。不过贝叶斯方法应该最多还是用在文本分类。