基于PSO与KF的无人机路径规划

基于粒子群优化与卡尔曼滤波的无人机海洋无线传感器网络节点运动预测数据采集

摘要

在本文中，我们考虑一个位于海面的无线传感器网络，其中节点因风和海流而漂移。在我们的场景中，将使用无人机（UAV）从传感器节点收集数据。目标是找到一条可飞行路径，该路径在传感器节点能耗、无人机与传感器节点之间的总信道吞吐量、无人机飞行时间以及无人机对节点的访问频率方面均达到最优。此外，该路径还应在节点位置估计不确定性方面实现最优。

采用卡尔曼滤波器（KF）来估计节点运动，利用粒子群优化（PSO）方法计算综合考虑上述各项目标的无人机路径。所提出的节点跟踪感知路径规划方案与另外两种场景进行了比较：一种是在所有时刻均基于节点位置的完全信息进行路径规划，另一种是基于节点的最后已知位置进行路径规划。

I. 引言

本文假设无线传感节点的电池容量有限，i.e.它们无法从周围环境中获取能量。这些节点能够感知并确定某些环境参数，例如水污染的空间和时间范围、有毒藻类区域、叶绿素浓度[1],盐度、浊度、pH[2],氧气密度或鱼类和哺乳动物活动。在某些应用中，必须建立一个连通网络以实现完整的功能，例如在线数据采集、实时数据分析以及触发事件功能。这样的网络需要高能耗来维持完全连通，从而导致节点和网络寿命缩短。

在其他场景中，由于测量值（例如盐度或海水中的化学成分）在不同位置之间差异较大，分布式无线传感器网络被部署到大面积区域。要使这种包含大量传感器的广域网络始终保持连接，将在能耗方面带来高昂成本。对于部署在极端或偏远地区的原位传感器网络，维护和数据采集都可能非常具有挑战性。

无人机（UAV）技术已广泛传播并流行于各个领域。与传统载人飞行器相比，最显著的优势是低成本、提高安全性以及易于部署。在无线通信中有许多应用利用无人机扩展通信范围、促进宽带5G网络发展，并通过小型无人机群辅助扩展蜂窝移动网络[3],，或从偏远地区或恶劣环境中的广域网络收集数据[4]。

II. 贡献与所考虑的场景

在文献中，例如[3],[5],[6]和[4]，通常认为无线传感器节点是静止的或具有有限的移动性。换句话说，假设节点的位置是固定的或已知的，并可用于路径规划。如果节点被部署后可随海面自由漂移，则该假设不再成立：由于节点会随着洋流漂移，持续与其保持连接以获取其位置更新通常是成本过高或不切实际的。主要目标是放宽上述假设。我们的主要贡献是将卡尔曼滤波器（KF）引入路径规划中，利用卡尔曼滤波器来估计和预测传感器节点的位置。当无人机处于通信范围内时，可以测量节点的位置。

我们还将研究能够获取额外洋流测量数据的情况。为了评估所提出的方法，我们将使用卡尔曼滤波器估计节点位置的方法（场景3）与另外两种场景进行比较。以下将描述这三种场景。

A. 场景1：完整的传感器节点位置信息

在此场景中，假设在任何时刻，无人机进行路径规划所需的节点信息均可获取。这意味着无人机将始终获得关于节点新位置的最新信息，因此可被视为能够取得最佳结果的理想情况。然而，由于节点是移动的，这要求节点反复向无人机发送其位置信息。这种做法存在两个不利之处：与无人机的额外通信将消耗传感器节点的能量，并且节点可能需要额外的设备（卫星通信设备）以实现远距离通信。

如果传感器与无人机完全互联，则传感器节点的位置信息可通过其他节点中继至无人机，但由于节点间通信的路径损耗较高，这仍会缩短传感器节点的使用寿命。

B. 场景2：受限范围的位置测量

在此场景中，无人机只有在进入通信范围后才能获取节点的新位置信息，因此会使用传感器节点最后已知的位置进行规划。当无人机能够与节点通信时，可以更新其飞行路径。

缺点是节点可能已经从先前已知的位置移动了较远的距离，这意味着无人机将需要花费更多时间从传感器网络中收集数据。在最坏的情况下，传感器节点甚至可能“丢失”，因为其新位置超出了无人机的通信范围，前提是无人机飞向传感器节点最后已知的位置。在这种情况下，无人机可以开始搜索这些节点，但这超出了本文的研究范围。

C. 场景3：基于估计的位置信息

在此场景中，无人机使用卡尔曼滤波器来估计和预测传感器节点的位置。通过基于风力和洋流预测的环境模型，无人机每次能够与传感器节点通信时，可根据节点之前的位置信息以及新测量数据来估计传感器节点的新位置。

D. 比较不同场景

为了公平比较这些场景中的节点能耗，我们考虑在所有情况下使用相同的无线通信链路。仅在第一种场景中，采用可调发射功率的无线信号，以确保无人机在需要时总能与传感器节点通信。当无人机与某个传感器节点之间的距离超过最大通信距离（即在初始发射功率下）时，将调整传输功率以确保此情况下的通信。在另外两种情况下，只有当无人机与传感器节点处于通信范围内时，才建立通信链路。本文将实现这些场景并比较其性能。

III. 建模

A. 传感器节点运动模型

考虑 n个无线传感器节点。为简化起见，我们假设节点 i ∈的位置向量 xi ∈ R2由微分方程 x˙i= θ+ wi给出，初始条件为 xi(0) ∈ R2，其中 θ ∈ R2是环境影响（洋流和风）在东西和北方向上的速度向量， wi ∈ R 2是一个随机高斯白噪声向量。我们假设˙环境影响由 θ= wθ描述，其中 wθ ∼N(0, Qθ)， Qθ为协方差。我们还假设这些节点具有相同的速度，因为它们部署在同一区域，天气和洋流的变化较小。因此，描述所有传感器节点运动以及恒定速度向量的微分方程组可表示为

x˙= Ax+ w:=
$$
\begin{bmatrix}
0_{2×2n} & I_{2×2} \
\cdots & \cdots \
I_{2×2} & 0_{2×2n}
\end{bmatrix}
x + w
$$
(1)

where x= (x >
1 , x >
2 ,…, x >
n , θ) > and w= (w >
1 , w >
2 ,…, w >
n , w θ)

B. 测量模型

我们考虑两种不同的传感器模型。在一种情况下，传感系统通过天气预报或其他传感设备获取有关影响传感器网络的风速和洋流速度的一些信息。在另一种情况下，我们假设没有此类测量数据可用，但可以根据传感器的测量位置，在环境效应为缓慢变化或恒定的假设下，对相关信息进行一定程度的估计。

1) 无速度向量测量的测量模型：

我们假设仅当无人机处于节点的通信距离内时，才能测量节点的位置。这被建模为

yi(tk)= xi(tk)+ vi(tk) if ∥ ∥p(tk)− xi(tk)∥∥≤ Lmax(2)

其中， tk是一个特定的时间实例， yi ∈ R 2是节点i ∈{1,…, n}的位置测量值，该测量值包含加性多元零均值正态分布噪声，其协方差为Ri，即 vi ∼ N(0, Ri)。此外， p表示无人机的位置，而 Lmax（将在第三节‐C中详细说明）表示系统的最大通信距离。引入 Lmax仅是为了简化我们场景的仿真。传感器通常监听来自无人机的广播信号，并在其传输时间的实际距离小于 Lmax时，周期性地发送其位置以及其他感知数据。同样为了简化，我们假设传感器配备有全球定位系统，类型相同，并且每次传输使用相同的数据长度。我们强调，可以开发更复杂的网络，其中包含使用不同数据长度的各种类型的传感器。还请注意，这些测量值取决于无人机与传感器节点之间的相对距离，因此是异步的。无人机将利用卡尔曼滤波器对节点位置进行估计。

2) 带有速度矢量测量的测量模型：

在此情况下，我们将假设具有测量模型（2），并且此外

yθ= θ+ vθ (3)

因此， yθ ∈ R 2 是带有加性多元零均值正态分布噪声的环境效应测量值，其协方差为 Rθ，即 vθ ∼ N(0, Rθ)。我们可以假设这些测量值仅在无人机处于某个气象站或类似设施的通信距离内时才可获得，如公式(2)所示，或者以一定的刷新率获得。

C. 无线电范围和发射功率

本节重点讨论传感器节点与无人机之间的通信中最大无线电传播距离和可调发射功率。为了在第二节的三种情况下实现传感器节点与无人机之间的通信，关于通信覆盖范围仅存在两种不同情况：a) 节点始终以固定功率水平发射，通信发生在最大无线电范围内（即场景2和3）；b) 节点可以调整传输功率以维持与无人机的持续连接（即场景1）。

前者可能无法确保无人机始终获取节点的位置信息和感知数据，但会减少节点的能耗。后者虽然与无人机建立了安全的通信链路，但会导致节点能耗增加。

1) 最大无线电覆盖：

首先，可以从以下公式找到无人机和传感器 s 之间的接收无线电信号强度 Prus ：

Prus= Pt0+ Gus − PLus (4)

其中，PLus表示无人机与传感器节点之间信道的传播路径损耗， Gus表示传感器节点和无人机两端的总天线增益，Pt0表示节点的固定发射功率。当接收信号功率达到其最小要求值时（即信息仍可解码，且Prus= Pr min），获得最大无线电范围。此时信道的传播路径损耗达到最大值，即PLus=PLmax，其表达式为：

PLmax= Pt0+ Gus − Prmin (5)

其中Prmin为允许的最小接收信号功率（单位：dBm）。

由于假设无人机与传感器节点之间的信道为视距(LOS)，因此无人机与传感器节点 Lus之间的距离（单位：米）与路径损耗PLus的关系为[7]

PLus= −147.55+ 20 log f+20 log Lus (6)

其中 f是赫兹为单位的无线电频率。PLus=PLmax使用公式(6)中的值，并结合公式(5)中的PLmax，可求得最大距离 Lus，我们将该距离记为 Lmax。

2) 传感器节点发射功率调整：

为了在传感器节点与无人机之间建立连续通信信道，需要调整传感器节点的发射功率。当接收信号强度高于最低要求的Prmin时，无需进行传输功率调整。如果低于该值，则必须调整发射功率Pt以满足：

Pt= PLus+ Prmin − Gus (7)

其中PLus是根据公式(6)计算的实际距离 Lus下的路径损耗，该距离是传感器节点基于无人机广播的位置消息估计得到的。

D. 信道容量和能耗

考虑到本文中的场景，无人机与传感器节点通常处于视距（LOS）状态，但在数据感知周期内，经常会出现信号障碍，例如由无人机的机身或其他辅助部件引起。因此，误码率（PER）会随着实际信噪比(SNR)的瞬时变化而变化。为了估算无人机从某一节点获取的数据量，需要计算信道带宽和误码率。平均误码率可按以下方式估算[8]：

PER γ = 1 − e −
a N
γ Γ(1+ b N
γ
) (8)

with

a N = log 10(Lp c m)
k m
, b N = 1 k m
(9)

其中 γ为平均信噪比， Γ(.) 是标准伽马分布函数，Lp是数据传输协议中使用的数据包长度（单位：比特）， cm和 km是取决于信号传输所采用调制方式的常数（例如，若调制方式为频移键控(FSK)，则km= 1 2和cm= 1 2；若调制方式为二进制相移键控(BPSK)，则km= 2和cm= 1）。

如果 Q是由于错误比特导致的数据包重传次数，则在时刻 t无人机从传感器s接收到的数据的平均误码率为

PERu,s,t= 1 −(1 − PERγ)Q (10)

传感器 s与无人机 u之间在时刻 t的信道平均比特误码率（BER）在存在错误比特重传的情况下由以下公式给出

BERu,s,t= 1 −(1 − PERu,s,t) Lp/Q (11)

由于无人机与传感器节点之间的信道在时域上快速变化，因此信道容量可被描述为，参见[8],

Cu,s,t= BW∫ ∞ 0
log(1+ t)
1 γ e
−t
γ dt (12) 其中BW为数据带宽。如果 T是传感器节点 s在时刻 t与无人机进行数据通信的时间持续长度，则无人机接收到的数据可表示为

Du,s,t,T= ∫ T 0
Cu,s,t(1 − BERu,s,t)dt (13)

由于传感器可能不会被无人机频繁访问，我们假设每个传感器在每次访问期间都会利用整个周期T来传输感知数据。

无人机从网络中所有传感器接收到的总数据为

Dtotal=
n
∑
i=1
N i
∑
j=1 Du,i,j,T (14)

其中Ni是网络中的传感器数量，以及无人机与传感器节点i进行数据通信的次数。

IV. 粒子群优化算法

粒子群优化（PSO）是一种在[9]中提出的随机群体优化方法。通信与网络是一个广泛应用PSO来解决网络性能优化问题的领域[10][11][12]。PSO还被用于无线传感器网络，以有效构建节点簇，优化数据采集、能量消耗和网络寿命，参见[12]和[13]。它还可用于为无人机从广域传感器网络进行数据采集时提供路径规划方案[4]。

本文中，粒子群优化用于在传感器节点随海面漂移时，为可飞行的无人机路径寻找最佳航路点。在粒子群优化算法中，考虑了以下目标：a) 传感器网络的总能量消耗；b) 无人机在飞行期间从传感器节点接收到的总数据；c) 无人机的总飞行时间；以及 d) 传感器节点感知数据的新鲜度。航路点的选择基于对目标函数的优化

f= α1fE+ α2fD+ α3fT+ α4fF (15)

其中 α1、 α2、 α3和 α4为正标量权重常数， fE、 fD、 fT和 fF是如下所述的函数

A. 传感器总能耗，f E

该值在不同场景下的解释如下。

1) 场景2和3：

每个节点将以恒定的发射功率Pt0传输其数据。假设一旦节点开始传输数据，将持续一个完整的 T周期，因此传感器网络的总能量消耗为

ES total=
NS
∑
i=1 NiPt0 (16)

2) 场景1：

每个节点将以发射功率Ptu,s,t传输其数据，该发射功率取决于与无人机的距离（定义见公式(7)）。

ES total=
NS
∑
i=1
Ni
∑
j=1 T Ptu,j,t (17)

B. 接收到的总数据， fD

公式（14）表示无人机在飞行期间从传感器节点接收到的总数据量。

C. 无人机飞行时间， fT

这是无人机沿其轨迹以计算出的航路点飞行所需的时间。轨迹通过这些航路点使用杜宾斯路径生成，[14]。杜宾斯路径由三段运动序列组成：直线、以及以车辆最大转向角向左或向右转弯。总飞行时间 fT(15)假设与杜宾斯路径的长度成正比，且无人机在整个仿真周期内保持恒定的地速。

D. 采集数据的新鲜度， fF

通常情况下，传感器节点会尝试周期性地传输感知数据，如果无人机在其通信范围内，则无人机可能会从该节点接收到部分数据。由于无人机的移动性以及其他障碍物的影响，无人机与节点之间的快速时变信道可能导致数据无法始终被正确接收。在这种情况下，节点需要等待无人机下次访问；当再次出现与无人机进行数据通信的机会时，该节点将具有更高的优先级。在仿真中，该优先级等于该节点自上次被无人机访问以来的等待时间。

V. 仿真

表I列出了在仿真中用于场景间性能比较的参数列表。

参数	值	参数	值
n	4	NWP	10
hu	120 米	vu	10 米/秒
Gi	10 分贝‐各向同性	Gu	10 分贝‐各向同性
Gj	10 分贝‐各向同性	lctr	20 位
Pt0	5 mW	f	5.8 吉赫
B	5 兆赫 ±150米	Prmin	‐90 dBm ±150米
x0		y0
I0	‐95 dBm	Q	5
cm	1	km	2
Lp	20 字节	Lmax	355 米
T	10 s 1000 焦耳	NIterations 仿真	5000 次
E0			10000 秒
α1	5	α2	10^7
α3	10^−2	α4	1

Lctr是数据协议中的控制比特数； x0和y0是传感器节点初始位置呈均匀分布的坐标范围； hu和 vu是无人机的飞行高度和地速。在场景3中，当测量速度向量时，假设其更新周期与位置更新周期相同，即 T。实际信噪比将根据实际接收信号强度与其最小允许值之间的差值计算得出 （Prmin）。对于适应度函数(15)中的加权常数（α1至 α4），其取值使得各项成本的影响大致归一化。表I中给出的值已用于仿真。

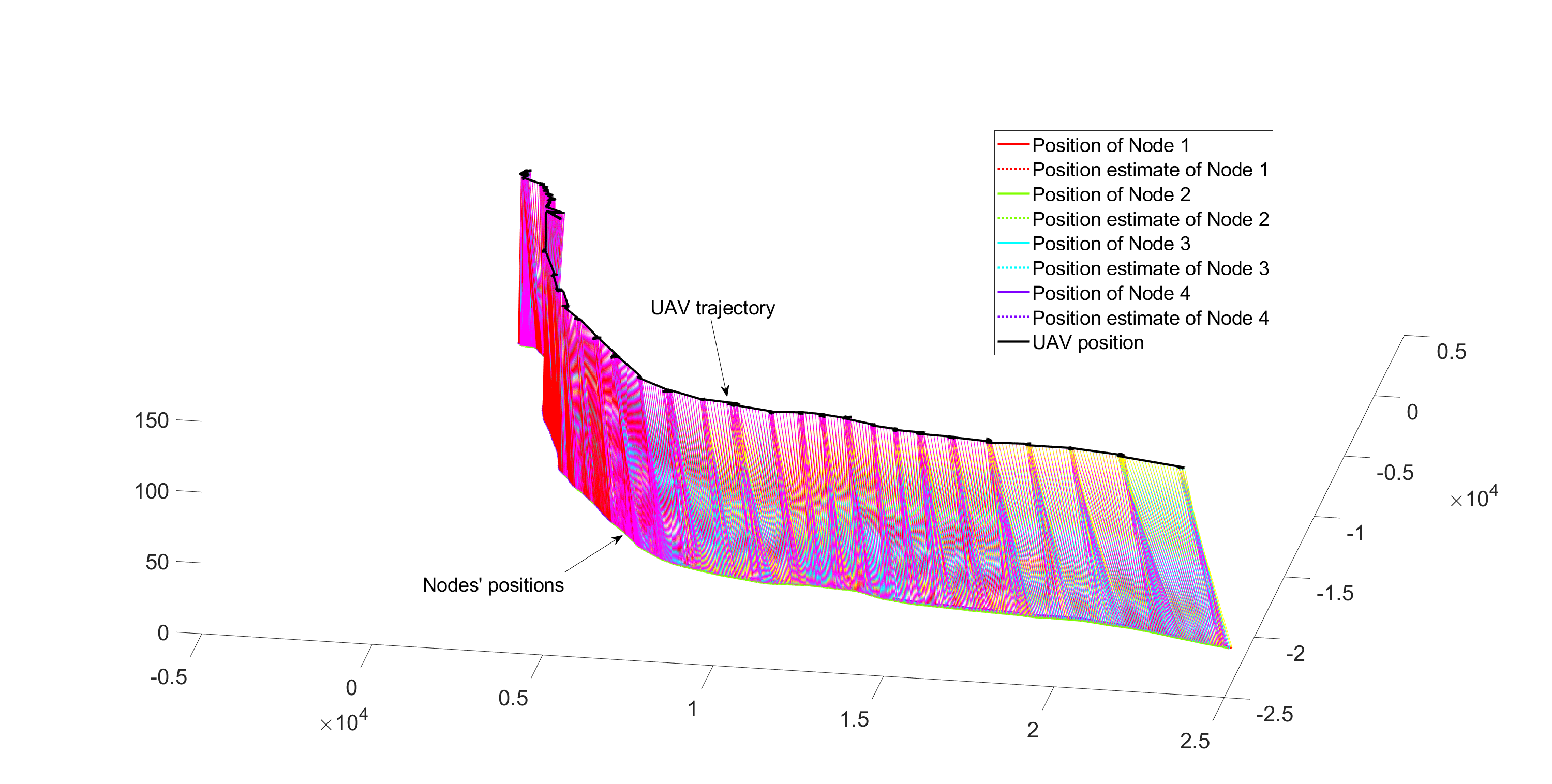
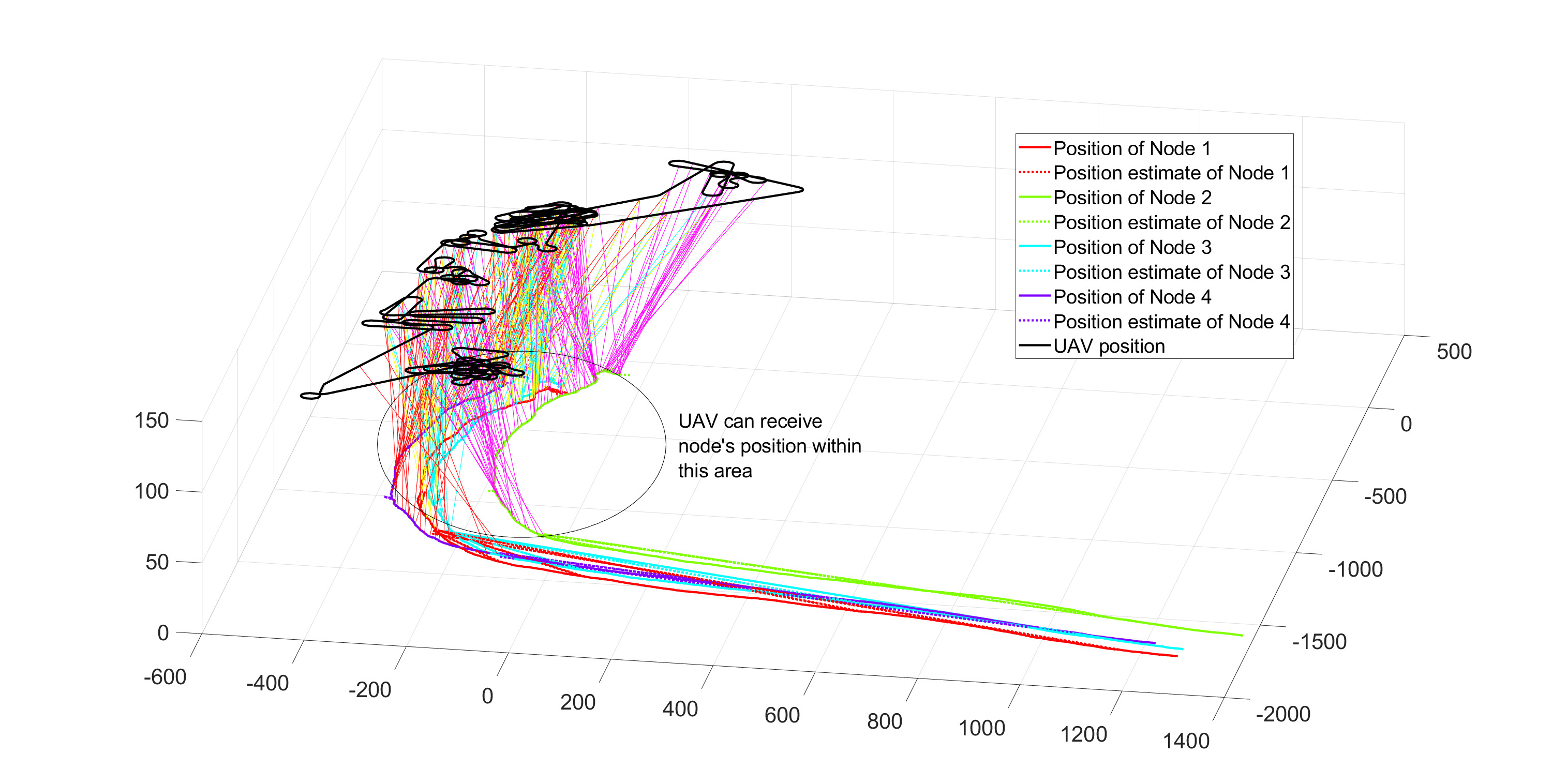
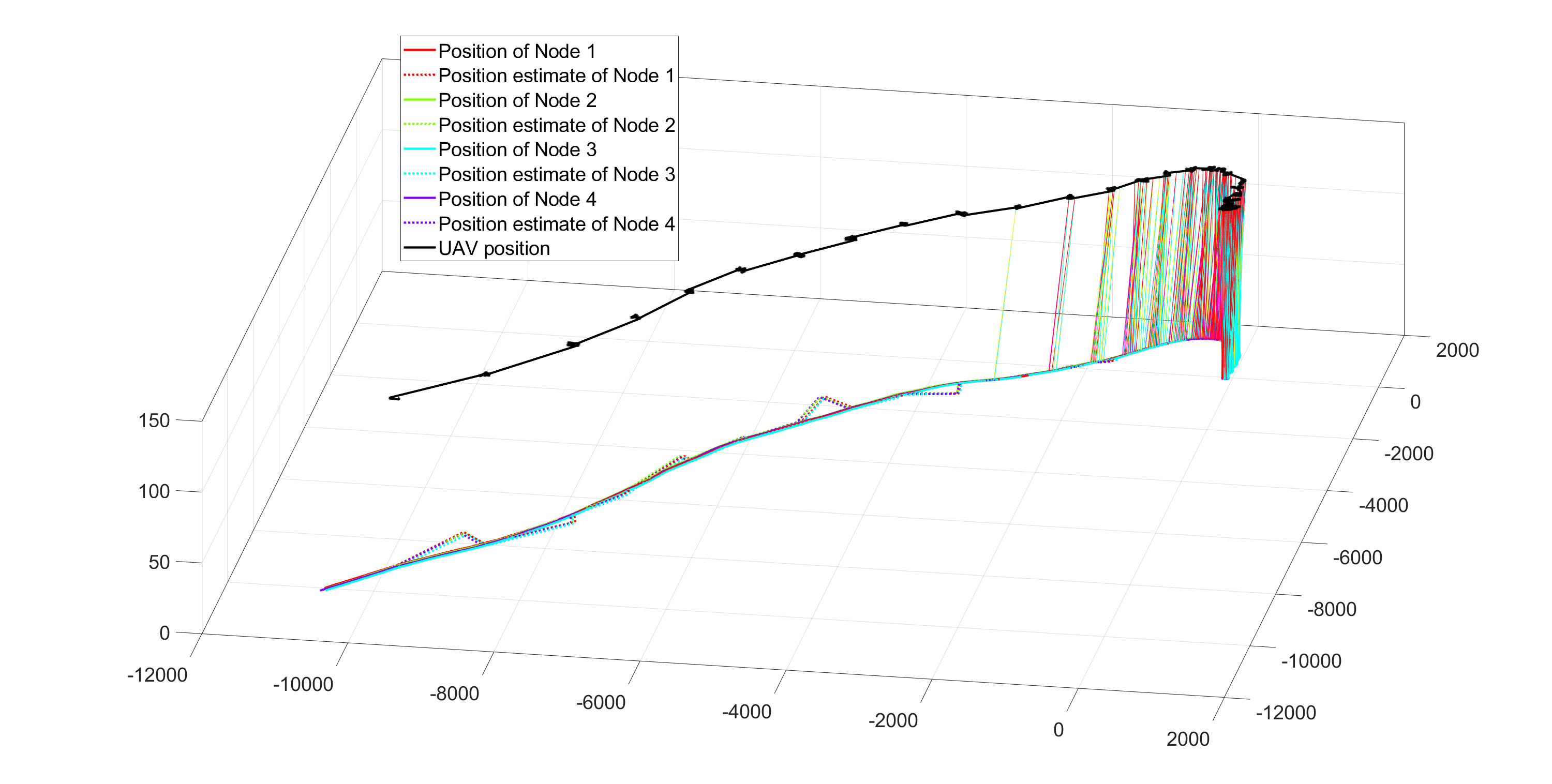
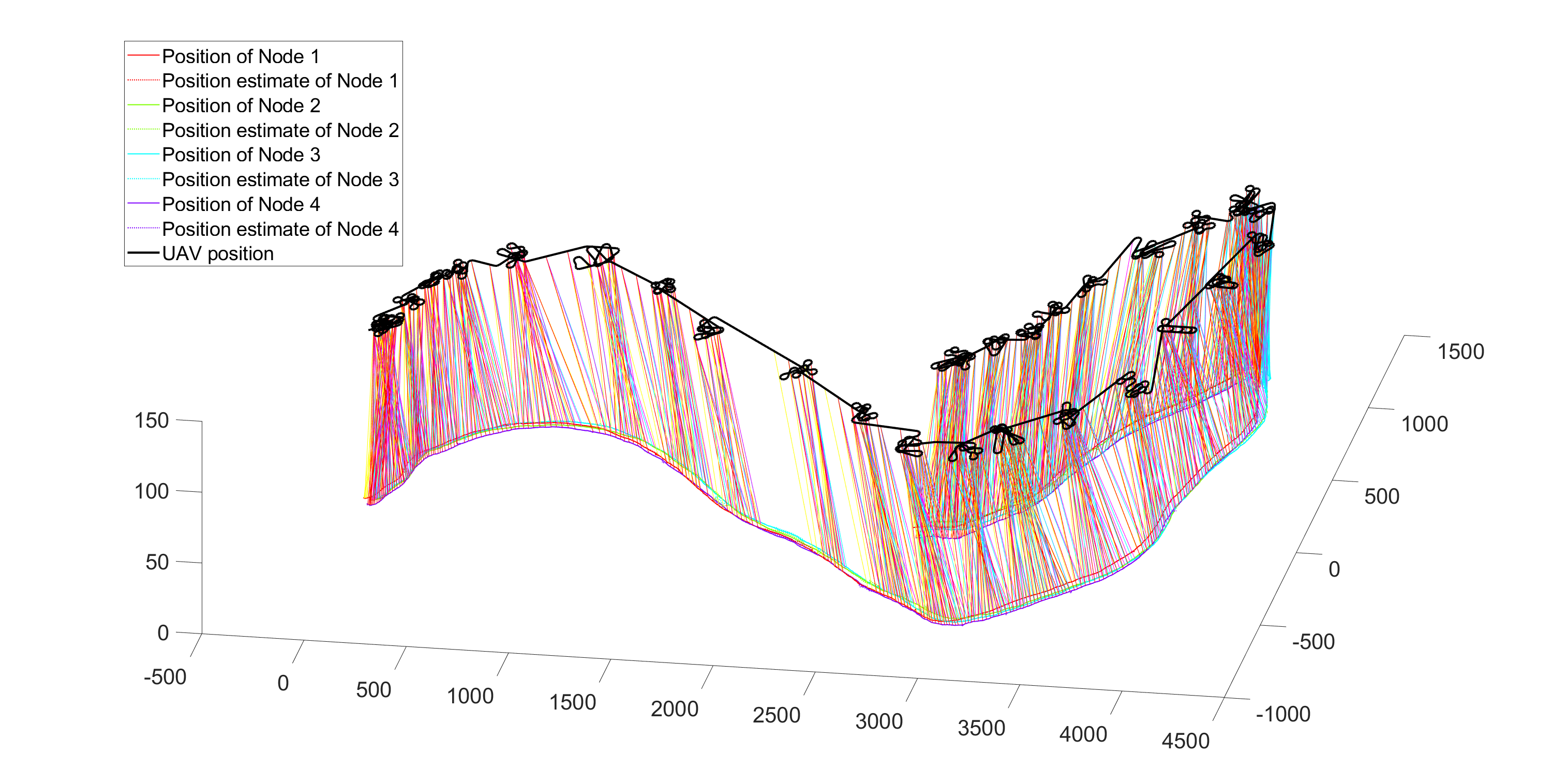
每种场景主要有两项评估。第一项展示了仿真周期内无人机的轨迹和节点的移动情况。对于一个传感器节点，有两个点分别表示其实际位置和估计位置。在此类图中，当无人机与传感器节点处于通信范围内时，也会绘制连接它们的线段。另一张图展示了场景1、2中节点位置的测量误差以及场景3中节点位置的估计误差。

A. 场景1：完整的传感器节点位置信息

在这种情况下，无人机可以在每个周期 T 内进行通信并获取节点的位置。由于这可能会导致传感器节点的高能耗，因此将展示每个节点的总能量消耗图，并用于与其他情况下节点仅以固定发射功率传输的情况进行比较。图1 显示，由于本案例中传感器节点的位置传输周期为 T= 10s，实际节点位置与其测量值之间仍存在较小差异。这一点在图2中得到可视化体现，其中最大差异约为50米。当减小传输周期时，这种差异将会减少，但相应地会增加节点的能耗。关于能耗，如表I所示，当传输周期为 10s时，图3表明，在接近3小时的飞行仿真时间后，每个节点所需的能量在70至100焦耳之间，平均每传感器为90焦耳。如果将该周期减小至 1s，则每个传感器节点消耗的能量平均约为900焦耳。

在这种情况下，节点位置误差将大大减小，可以说无人机掌握了传感器节点的全部信息。然而，传感器节点在短暂运行后电池就会耗尽。这是该网络场景实施中的一个主要限制。

B. 场景2: 受限范围的位置信息

此处，仅当以周期 T 的时间间隔建立通信链路时，节点的位置和传感器数据才会传输给无人机。因此，无人机的轨迹将取决于节点位置的最后一次更新。由于节点移动性，实际节点的位置与所使用的相关信息之间可能会存在较大偏差。

图4显示了此场景下节点的运动和无人机的轨迹。在最初的15分钟内，无人机能够定期从所有传感器节点接收位置信息。在此之后，实际节点位置与最后一次更新之间的误差开始急剧增加，无人机开始失去对部分节点的跟踪。由于无人机仅继续飞越最后已知位置，位置误差持续增加，如图5所示。例如，在1.5小时的仿真时间后，节点的位置误差可能增加到高达10公里。单个节点的平均能耗约为0.9焦耳，大约是第一种情况的百分之一。

C. 场景3：基于估计的位置信息

为了在保持较低能耗的同时提高对节点位置的了解，本场景中应用了卡尔曼滤波器。需要注意的是，无人机仍需处于节点的通信范围内，才能对卡尔曼滤波器进行测量更新。该场景将考虑两种测量模型，即如第三节‐B所述，包含和不包含速度矢量测量的测量模型。

1) 没有速度矢量测量时：

与场景2相比，应用卡尔曼滤波器使无人机掌握节点运动信息的良好时间段延长了一倍（见图6和图4）。节点位置测量的误差比场景2小十倍（见图7和图5），但其不准确性仍然逐渐导致无人机的轨迹远离节点的实际位置（见图6）。尽管这种情况比场景2发生得晚，但无人机仍然会丢失传感器节点。

2) 带有速度矢量测量时：

如果有可能在无人机上更新速度向量，则卡尔曼滤波器将显著改善位置估计误差。图9显示，最大位置误差与场景1中达到的结果非常相似（可对比图2）。精确估计使得无人机能够持续跟踪传感器节点的移动，参见图8。

VI. 结论

使用速度矢量测量的卡尔曼滤波器在两种场景下均优于其他两种方案：在传感器节点的能耗以及无人机跟随节点运动的能力方面，该方案与采用自适应发射功率所达到的节点运动预测效果相同，但显著降低了节点的能耗。这种方法的主要挑战之一可能是实现速度矢量的测量。此外，尚不清楚卡尔曼滤波器中使用的线性模型是否能够充分逼近真实世界场景中的节点运动。这些方面将在未来工作中进行研究。我们还将考虑使用多架无人机从空间分布更广的传感器网络中进行数据采集。