基于抛物线角度的起重机防摆控制

基于抛物线角度的防摆控制用于具有有限动态载荷的集装箱起重机

摘要

提出了一种新型的起重机防摆控制系统。该方法基于将预定偏转角构造成分段连续抛物线函数，其二阶导数无不连续性，三阶导数为具有特定变号幅值的矩形脉冲，从而消除了起重机结构和运动齿轮中的机械应力。该方法可在悬挂负载的水平运动（在两个正交坐标中）以及起升/下降过程中提供振荡阻尼。该控制方法对机构/有效载荷质量比、提升高度和起升速度具有不变性。

关键词

防摇系统；运动控制；振荡阻尼；集装箱起重机。

1 引言

港口和船到岸集装箱起重机的快速可靠运行对港口码头效率具有重要影响。为了提升起重机性能，需要对起重机在稳态和动态运行模式下的操作进行深入研究和详细分析。因此，已建立了多个不同复杂程度的数学模型，用于模拟各类起重机的操作（阿卜杜勒‐拉赫曼等，2003年；方等，2003年；马等，2010年；孙等，2011年；余等，2011年；孙和方，2012年，2014年；金等，2012年；赵和高，2012年；方等，2014年；吴和夏，2015年）。

这类起重机的装卸周期大部分时间都用于运行，即将负载沿吊臂从船舶移动到岸边或反向移动。在提升高度20–50米的情况下，由于悬挂负载的摆动，小车运行机构表现出相对较长的瞬态过程，阻尼此类振荡可能需要20–30秒。因此，为实现可靠高效的起重机操作，必须采用防摆控制。

近年来，已开发出多种防摆控制系统，以减轻起重机作业过程中的负载振荡。

2014年，马苏德等（2014a，2004b）提出了一种起重机的动态非线性模型，用于抑制货物摆动。朔布（2008）提出了一种基于速率的控制策略，仅利用惯性测量单元信息直接计算所需的起重机关节速度，以实现使有效载荷隔离船舶运动。坎达吉和兹德罗齐斯（2008）则应用了庞特里亚金原理结合恒定力和阶跃切换技术。

加里多等（2008）利用在线二维倾角仪测量和输入脉冲序列的在线计算，实现了输入整形在防摆控制中的应用。所开发的输入整形控制分为两个阶段：直线运动和外部扰动消除。朴等（2008）提出了一种自适应模糊滑模控制（AFSMC），用于桥式起重机在系统不确定性和执行器非线性影响下的鲁棒防摆轨迹跟踪。崔（2009）实现了一种非线性跟踪控制律，以消除系统的非线性特性，并在存在初始摆角和有效载荷重量变化的情况下，实现满意的定位控制和摆动抑制。寺岛等（2010年）考虑了船舶摇摆和负载摆动，研究了一种结合船舶行为的回转式起重机集成计算机仿真工具。该集成模拟器通过结合外部力实现与流体分析软件的组件接口程序。金等人（2011）提出了一种采用双级控制系统的防摆控制器。系统参数通过针对1/20比例D4起重机模型的系统辨识过程确定，并基于X轴和Y轴的解耦以及线性化起重机模型设计了用于防摆的LQR控制器。

最近，吴和洪（2012b, 2012a）、段等人（2013）以及朴等人（2014）讨论了集装箱起重机的滑模控制。所设计的滑动面将负载的摆动运动纳入小车动力学中，控制律采用变增益形式。在段等人（2013）中提出了一种起重机系统滑模控制的自适应版本，考虑了未知负载质量和阻尼元件的情况。利用小车驱动力和货物提升力两个输入，所提出的自适应鲁棒控制器同时执行四项任务，包括跟踪小车、提升货物、在瞬态过程中保持货物摆动较小，以及在稳态目标位置完全消除负载角度。

模型预测控制（MPC）控制器可实现快速搬运货物并减小摆动，如约列夫斯基和贝戈（2015）所述。MPC控制器的性能指标函数通过多目标优化求解。张等人（2016）研究了在二维（2D）空间中针对欠驱动起重机系统的有限时间调节控制器，涵盖恒定绳长和变化绳长两种情况。所设计的控制器能够在有限时间内同时抑制负载摆动并将小车调节至目标位置，适用于恒定绳长情况下的二维桥式起重机系统。

在埃尔米多罗等人（2016）的研究中表明，负载振荡行为取决于绳索长度，因此提出了一种增益调度控制律以减小这种影响。具体而言，为了考虑控制器实现中的技术限制，设计了一个固定阶次控制器，并同时施加了鲁棒性和性能约束。

在李（1998）中，考虑了一种桥式起重机的三维模型，其控制律基于起重机和摆动负载的动能和势能的广义方程。为了补偿振荡，综合了一个控制器，其传递函数与具有两个自由度的线性化摆模型互为逆关系。为了控制起重机的运动，需要测量负载的摆角、负载质量、水平运动机构的可移动部分质量以及小车质量。

同样在坎波‐勒库尔等人（2016）的研究中，需要精确可靠的绳索角度测量以及起重机系统的完整动力学模型。随后提出了不同的技术来估计有效载荷加速度，以提高控制器性能。

解决防摆问题的一种可能方法是应用庞特里亚金原理（Khandakji 和 Zdrozis，2008；Busher 等，2015），该方法考虑了施加到控制对象的控制输入的约束，并在系统最优响应的综合中提供最有效的结果。然而，所得到的解在最大值和最小值之间采用多路开关控制，需要精确测量负载与机构的质量比、悬挂负载的瞬时高度及其在过渡过程中的持续性过程。在实际应用中，此类限制会对所用设备提出额外要求，并妨碍操作员的操作自由。因此，要成功抑制负载振荡，需要采用一种允许多个机构（水平运行和起升）同时操作的控制方法。另一方面，该控制方法应对有效载荷测量参数的误差以及任何可能的随机干扰具有最低的敏感性。

本文提出的防摆控制方法仅需测量绳索长度；其他所有参数均可从机构额定参数中获取，无需测量。通过向行走电动驱动输入速度参考信号来实现防摆控制。

2 小车和负载的运动模型

小车运行机构或起重机水平运动的数学模型可表示为一个带有长度为L（悬挂点与负载重心之间的距离）的不可伸长无质量绳索的两质量机械系统。考虑到针对大多数工业起重机所作的简化假设（sin α ≈ α，cos α ≈ 1），该模型中的动力学可通过以下微分方程组来描述：

$$
F(t) = m_C \ddot{p}_C + m_L (\ddot{p}_C - L \ddot{\alpha} - g \alpha)
$$

其中，$p_C$、$p_L$ 分别表示小车上的悬挂点和负载的位置。$\alpha$ 表示绳索相对于垂直方向在 $x$ 或 $y$ 轴上的偏离角（摆动），$F(t)$ 为电动驱动装置产生的力；该力是作用在悬挂点上的控制作用（图1）。

当小车受到力 $F(t)$ 作用时，系统的等效传递函数的分母为：

$$
Q(s) = s^2 + \frac{(m_C + m_L)g}{m_C L}
$$

动态系统的动态特性取决于质量比率。

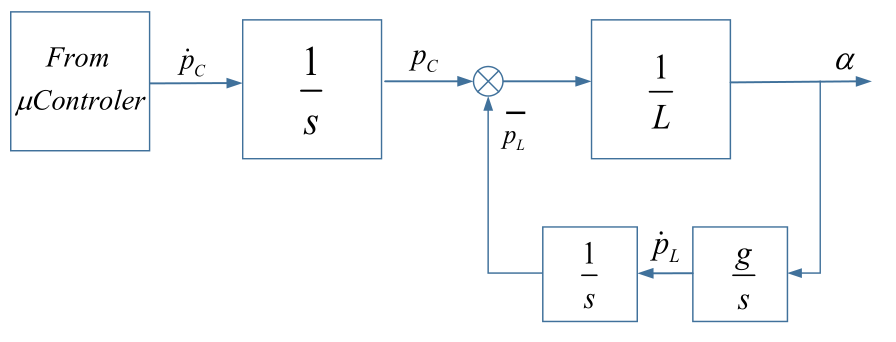
但当控制悬挂点速度时，动态过程根据图2所示的框图进行描述。

在这种情况下，传递函数的分母不依赖于负载和起重机的质量：

$$
Q(s) = s^2 + \frac{g}{L}
$$

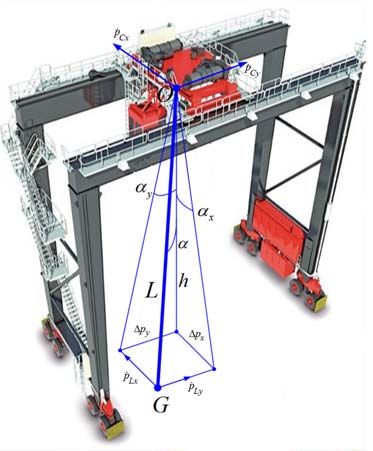
(a) 货物沿控制台的纵向移动（岸桥集装箱起重机）
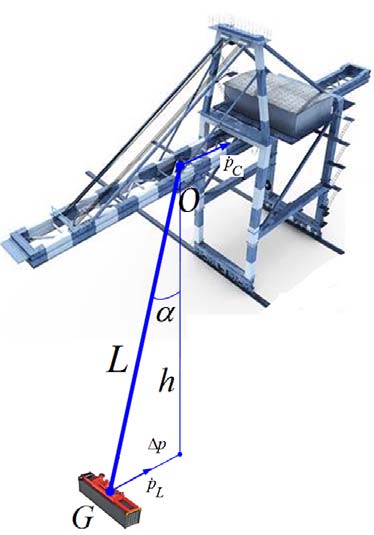
(b) 复合运动操作（后装式集装箱起重机）

3 防摆控制

控制目标是建立一种协调控制律，以确保在起重机运行过程的瞬态结束时消除负载摆动。一种对起重机运动部件与负载的质量比具有不变性的方法是通过特定函数来控制负载悬挂点的速度。在此方法中，根据公式(1)，利用预定义函数$\alpha$，负载速度$v_2$可定义为$\alpha(t)$的积分：

$$
\dot{p}_L(t) = g \int_0^t \alpha(\tau) d\tau
$$

对方程 $\alpha L = p_C – p_L$ 进行微分，得到悬挂点速度的速度函数：

$$
\dot{p}_C(t) = \dot{p}_L(t) + L \dot{\alpha}(t) + \int_0^t \alpha(\tau) d\tau
$$

对于(3)，选择一种控制方法，其中角度$\alpha$由一个光滑连续二阶可微函数定义，该函数应具有零初始和终值条件，包括一阶导数。

这种控制律最重要的特点是速度函数与负载质量和悬挂点质量无关。这一特点使得该控制律可以应用于负载质量变化较大的机构中，这在集装箱起重机中十分典型。同时，根据负载类型的不同，集装箱的重心可能相对于集装箱的几何中心发生轻微偏移，最大可达±0.5 m。

4 防摆控制的角余弦定律

其中一组此类函数是，例如，谐波函数：

$$
\alpha(t) = \alpha_m \left(1 - \cos\left(\frac{t}{T_G}\right)\right)
$$

其中 $\alpha_m$ 为绳索垂直偏转最大角度的一半，$T_G$ 为时间常数，即负载振荡角频率的逆。

根据公式(4)，当偏转角较小时（sin $\alpha$ ≈ $\alpha$，cos $\alpha$ ≈ 1），负载的速度将从初始值$V_0$变化至最终值$V_E$，其变化规律如下函数所示：

$$
\dot{p}_L(t) = V_0 + g \alpha_m T_G \sin\left(\frac{t}{T_G}\right)
$$

其中 $\alpha_m g = a$ 为负载和小车在一个振荡周期内的平均加速度。

悬挂点速度通常必须满足以下条件：

$$
\dot{p}_C(t) = \dot{p}_L(t) + L \dot{\alpha}(t)
$$

因此，如果加速度可以根据以下公式计算：

$$
a = \frac{V_E - V_0}{2\pi T_G}
$$

然后，在时间 $t= 2\pi T_G$ 之后，我们得到 $ \alpha = 0, \dot{\alpha} = 0 $。

如果$2a$的值超过加速度限值，则应注意，在$t = \pi T_G$时刻，角度$\alpha$达到其最大值 $\alpha= 2\alpha_m$，此时负载的加速度达到最大，且等于$2\alpha_m g$。如果此时将小车的加速度更改为负载的加速度值，则偏转角$\alpha$将保持不变。

因此，我们得到了运行机构的控制律，该控制律由三个阶段组成：
1. 从初始状态$\alpha= 0$加速至预定的设定速度，实现负载相对于垂直方向的零偏差；
2. 以设定速度进行稳态运行，保持$\alpha= 0$；
3. 制动直至静止，达到负载相对于垂直方向的零偏差。

如果第一和第三区间的持续时间最小化，则瞬态的持续时间最小，因为在此期间机构和负载的平均加速度比第二阶段小两倍。

根据行走驱动装置产生的最大允许力 $F_{max}$ ，$T_G$ 应满足以下条件：

$$
T_G = \sqrt{\frac{L m_C}{2 g (m_C + m_L)}}
$$

其中 $m_L$、$m_C$ 分别为负载和起重机在选定方向上的运动部件的标称质量。

因此，第二区间的时间持续时间为：

$$
t = \frac{V_E - V_0}{a} - 2\pi T_G
$$

第一和第三区间内加速度的线性分量：

$$
a = \frac{F_{max}}{2(m_C + m_L)}
$$

在瞬态过程中绳索长度保持固定，由方程(5)和(6)可得悬挂点速度在三个时间段内的关系：

$$
\dot{p}_C(t) =
\begin{cases}
V_0 + at - \frac{aL}{gT_G} \sin\left(\frac{t}{T_G}\right), & 0 \leq t \leq \pi T_G \
V_E - a(t - \pi T_G), & \pi T_G < t \leq \pi T_G + t \
V_E - a(t - \pi T_G) + \frac{aL}{gT_G} \sin\left(\frac{t - \pi T_G}{T_G}\right), & \pi T_G + t < t \leq 2\pi T_G + t
\end{cases}
$$

运行机构产生的力可由公式(1)推导得出：

$$
F(t) = m_C \ddot{p}_C + m_L (\ddot{p}_C - L \ddot{\alpha} - g \alpha)
$$

相应地，对于三个时间段中的每一个，我们得到：

$$
F(t) =
\begin{cases}
m_L g \left[ \frac{L}{T_G^2} \cos\left(\frac{t}{T_G}\right) + \frac{v_L t}{T_G} \sin\left(\frac{t}{T_G}\right) \right] + (m_C + m_L) a, & 0 \leq t \leq \pi T_G \
(m_C + m_L) a, & \pi T_G < t \leq \pi T_G + t \
m_L g \left[ \frac{L}{T_G^2} \cos\left(\frac{t - \pi T_G}{T_G}\right) + \frac{v_L (t - \pi T_G)}{T_G} \sin\left(\frac{t - \pi T_G}{T_G}\right) \right] - (m_C + m_L) a, & \pi T_G + t < t \leq 2\pi T_G + t
\end{cases}
$$

其中

$$
v_L = \frac{dL}{dt}
$$

是钢丝绳长度的变化速度，即起升/下降速度。

取$v_L= 0$，可得到若干特征值，基于这些特征值可确定瞬态过程所需的参数：

$$
F(t) =
\begin{cases}
2a(m_C + m_L), & 0 \leq t \leq \pi T_G \
2a(m_C + m_L), & \pi T_G < t \leq \pi T_G + t \
-2a(m_C + m_L), & \pi T_G + t < t \leq 2\pi T_G + t
\end{cases}
$$

根据第二区间内的最大允许力 $F_{max}= 2a(m_C+ m_L)$，我们得到：

$$
a = \frac{F_{max}}{2(m_C + m_L)}
$$

以及第一和第三区间的最短持续时间：

$$
T_G = \sqrt{\frac{L m_C}{2 g (m_C + m_L)}}
$$

因此，得到了悬挂点速度的控制律。该控制律提供了结合起升和运行操作的可能性，且无需对负载质量进行精确测量。$T_G$可根据某些限制条件进行选择。质量偏离计算值仅在瞬态过程中引起力的变化。

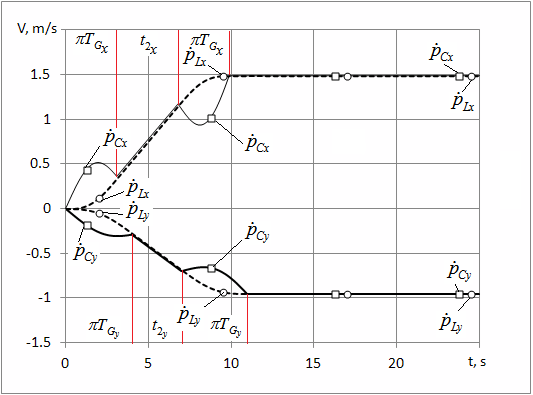
理论上，在机构加速度结束时，负载振荡不存在，但负载及其悬挂点的实际速度与计算值一致。图3展示了在绳索初始长度为35米、下降速度为1米/秒的瞬态过程中，同时在 、 坐标下实现的水平运动速度控制律公式(10)的应用情况。

由于不同的驱动装置和机构参数，时间间隔$2\pi T_{G,x}$, $t_x$, $\pi T_{G,y}$, $t_y$ 可能有所变化。显然，不存在残余振动($\Delta p_x, \Delta p_y$)。

显然，通过在预定位置进行定位，负载的预测行为使得起重机操作的自动化成为可能。

需要注意的是，在负载的偏离角中使用余弦函数(4)会导致在过渡过程(13)期间，电机转矩/力需多次发生幅值为±Fmax 的阶跃变化。这种控制律不可避免地会引起机械冲击，可能导致设备损坏并缩短机械传动装置和电机的使用寿命。

5 抛物线防摆控制

因此，应修改负载角度偏差函数，以消除电机轴上不允许的机械应力，并使用物理可实现的扭矩。一种可在现代变频驱动（VFD）或直接转矩控制（DTC）系统中实施的控制方法，能够保证在集装箱起重机中负载可能发生任意组合的垂直和水平运动时，有效抑制悬挂负载的振荡。

为了防止此类不良现象，并产生与变频驱动或直接转矩控制兼容的物理可实现的转矩定律，有必要构造满足连续性和二阶可微条件的函数 $\alpha(t)$。在此条件下，电机无需产生理想的变号转矩矩形脉冲。

根据式(2)、(3)和(12)，可提出一种基于预设偏转角的控制方法，该预设偏转角为分段连续函数，且其二阶导数连续。

然后，在加减速的初始阶段，通过将$\alpha(t)$的三阶导数构造成具有固定幅值和宽度且符号可变的矩形形式，可使二阶导数的变化呈现梯形形式。这进而决定了曲线一阶导数的形状，该曲线在初始和最终段由抛物线组成，中间为线性段。

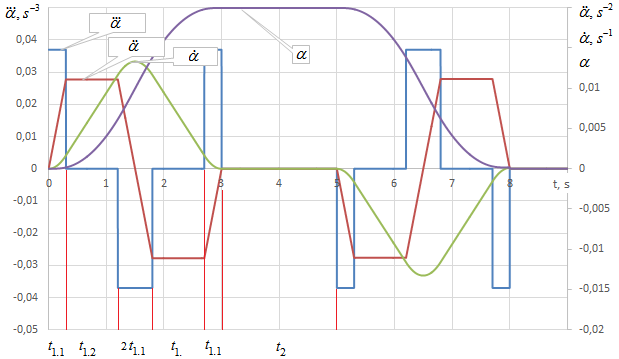
因此，曲线$\alpha(t)$的形状在初始和最终阶段包含三次抛物线，并在负载偏转角增加和保持期间结合了线性段。图4显示了该过程的初始部分，对应于图3中$\pi T_G$区间。

重要的是，控制系统必须根据电机轴上的允许变化率和最大转矩来设定区间$t_{11}, t_{12}$的持续时间以及三阶导数$\dddot{\alpha}_{max}$的幅值。其他坐标应由控制器使用任意数值积分方法进行计算。

$$
\dot{\alpha}(t) = \int_0^t \ddot{\alpha}(\tau) d\tau, \quad \ddot{\alpha}(t) = \int_0^t \dddot{\alpha}(\tau) d\tau, \quad \alpha(t) = \int_0^t \dot{\alpha}(\tau) d\tau
$$

为了计算所需参数，应分析时间间隔 $t_{1.1} – t_{1.2} – t_{1.1}$。

对于该区间，应满足以下条件：

$$
\max |F(t)| \leq F_{max}, \quad \left|\frac{dF}{dt}\right| \leq \frac{F_{max}}{2}
$$

基于关系 $\ddot{\alpha}(t)$：

$$
\ddot{\alpha}(t) =
\begin{cases}
\dddot{\alpha} {max} (t - t {1.1}), & t_{1.1} \leq t \leq t_{1.2} \
\dddot{\alpha} {max} (t {1.2} - t_{1.1}), & t_{1.2} < t \leq t_{1.1} + t_{1.2} \
\dddot{\alpha} {max} (2t {1.1} + t_{1.2} - t), & t_{1.1} + t_{1.2} < t \leq 2t_{1.1} + t_{1.2}
\end{cases}
$$

得到：

$$
\dot{\alpha}(t) =
\begin{cases}
\frac{1}{2} \dddot{\alpha} {max} (t - t {1.1})^2, & t_{1.1} \leq t \leq t_{1.2} \
\frac{1}{2} \dddot{\alpha} {max} (t {1.2} - t_{1.1})^2 + \dddot{\alpha} {max} (t {1.2} - t_{1.1})(t - t_{1.2}), & t_{1.2} < t \leq t_{1.1} + t_{1.2} \
\frac{1}{2} \dddot{\alpha} {max} (2t {1.1} + t_{1.2} - t)^2, & t_{1.1} + t_{1.2} < t \leq 2t_{1.1} + t_{1.2}
\end{cases}
$$

$$
\alpha(t) =
\begin{cases}
\frac{1}{6} \dddot{\alpha} {max} (t - t {1.1})^3, & t_{1.1} \leq t \leq t_{1.2} \
\frac{1}{6} \dddot{\alpha} {max} (t {1.2} - t_{1.1})^3 + \frac{1}{2} \dddot{\alpha} {max} (t {1.2} - t_{1.1})^2 (t - t_{1.2}) + \frac{1}{2} \dddot{\alpha} {max} (t {1.2} - t_{1.1})(t - t_{1.2})^2, & t_{1.2} < t \leq t_{1.1} + t_{1.2} \
\frac{1}{6} \dddot{\alpha} {max} (2t {1.1} + t_{1.2} - t)^3, & t_{1.1} + t_{1.2} < t \leq 2t_{1.1} + t_{1.2}
\end{cases}
$$

在边界点处，我们得到：

$$
\begin{aligned}
&\alpha(t_{1.1}) = 0, \quad \dot{\alpha}(t_{1.1}) = 0 \
&\alpha(t_{1.1} + t_{1.2}) = \frac{1}{2} \dddot{\alpha} {max} t {1.1}^2 t_{1.2}, \quad \dot{\alpha}(t_{1.1} + t_{1.2}) = \dddot{\alpha} {max} t {1.1} t_{1.2} \
&\alpha(2t_{1.1} + t_{1.2}) = \dddot{\alpha} {max} t {1.1}^2 t_{1.2}, \quad \dot{\alpha}(2t_{1.1} + t_{1.2}) = 0
\end{aligned}
$$

当$t = t_{1.1}+ t_{1.2}$时，力达到最大值；当$t = 2t_{1.1}+ t_{1.2}$时，偏转角等于最大值的一半。

已知$F_{max}=(m_C+ m_L)\ddot{\alpha}_{max} g$，在绳索长度恒定（$v_L= 0$）的情况下，由(11)可得：

$$
F(t) = (m_C + m_L)(\ddot{p}_C + L \ddot{\alpha})
$$

然后我们得到一个方程组：

$$
\begin{cases}
\frac{1}{6} \dddot{\alpha} {max} t {1.1}^3 + \frac{1}{2} \dddot{\alpha} {max} t {1.1}^2 t_{1.2} = \alpha_{max} \
\dddot{\alpha} {max} t {1.1} t_{1.2} = \dot{\alpha} {max} \
(m_C + m_L) L \dddot{\alpha} {max} t_{1.1} = F_{max}
\end{cases}
$$

前两个方程可以重写如下：

$$
\begin{cases}
\dddot{\alpha} {max} t {1.1}^2 (t_{1.1} + 3t_{1.2}) = 6\alpha_{max} \
\dddot{\alpha} {max} t {1.1} t_{1.2} = \dot{\alpha}_{max}
\end{cases}
$$

令等式右端相等，我们得到：

$$
t_{1.2} = \frac{3\alpha_{max}}{\dot{\alpha} {max} t {1.1}}
$$

将(23)代入(20)的第一个方程，并考虑第三个方程，可通过迭代方式求解如下：

$$
t_{1.1} = \sqrt[3]{\frac{6\alpha_{max} F_{max}}{(m_C + m_L) L \dot{\alpha}_{max}}}
$$

根据(20)的第三个方程，设力的变化率 $\dot{F} {max}$ 的最大允许值等于：$\dddot{\alpha} {max}$

$$
\dot{F} {max} = (m_C + m_L) L \dddot{\alpha} {max}
$$

最终，根据方程(22)，$t_{1.2}$被设定为：

$$
t_{1.2} = \frac{3\alpha_{max}}{\dot{\alpha} {max} t {1.1}}
$$

因此，瞬态参数 $\dddot{\alpha} {max}, t {1.1}, t_{1.2}$ 被确定。

此外，分别使用方程(2)计算负载速度和方程(3)计算悬挂点速度，进而作为运行机构控制系统中的速度设定信号。

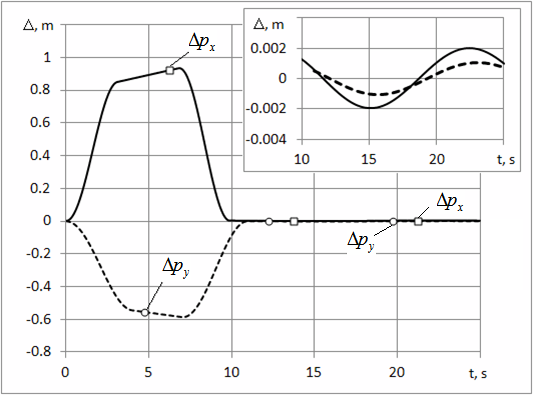
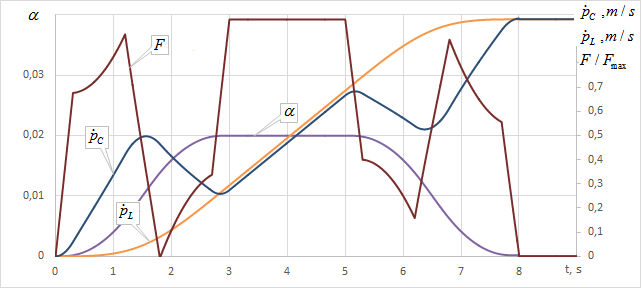
图5和图6分别给出了绳索长度恒定时运行机构的加速度示意图，以及水平运动与起升操作结合时的示意图。

从图4和图5可以看出，防摆控制不需要力的阶跃变化。这有助于减少起重机驱动装置中的冲击载荷，提高控制精度，并使力（电机转矩）的变化率与驱动系统的性能相协调。

所提出的防摆控制方法的一个显著特征是力（电机转矩）符号的恒定性，这使得该方法在现代变频驱动器或直接转矩控制中具有物理上可实现性。同时，在集装箱起重机中测量钢丝绳长度较为容易（大多数设备都配备了必要的传感器以确保操作员的舒适操作）。因此，所提出的控制方法可以精确地应用于此类起重机械。

6 实验装置和结果

为了验证仿真结果，设计了一台起升高度为1米、臂长为1.5米的集装箱起重机原型。

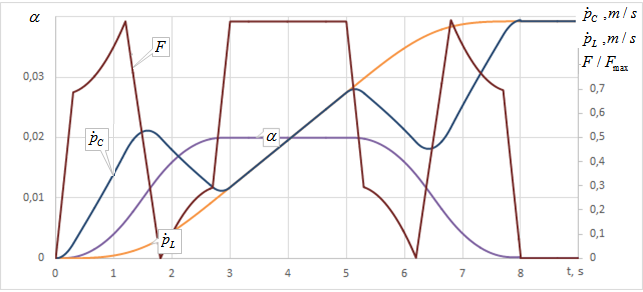
图7显示了集装箱起重机实验装置的照片。小车和起升驱动采用步进电机。电机通过四象限和两相驱动器使用Modbus协议连接到控制器，控制器再连接至 SCADA Citect 7。实验装置的测量与控制在DSP板上实现，采样时间为2毫秒。

运动算法在SCADA系统中生成，运动坐标在线显示在屏幕上。此外，对负载摆动的视觉观察是评估控制系统性能的主要因素。

在图8中，使用所提出的防摆控制方法执行了完整的运动周期，包括起升/小车驱动的启动、负载平移和停止。从相应的波形可以看出，在启动和停止结束时，负载摆动已显著衰减。对负载行为的视觉观察也证实了负载摆动的消除。

7 结论

1. 提出了一种基于抛物线角度的集装箱起重机防摆控制方法。该控制方法基于对有效载荷悬挂点的速度控制，可抑制悬挂负载在水平运动（两个正交坐标方向）和起升/下降过程中的振荡。该控制方法对机构/货物质量比和起升速度具有不变性。
2. 实验和仿真结果表明，在任何瞬态过程结束时，负载摆动均消失，同时实现负载的水平运动（两个正交坐标方向）和垂直运动（起升/下降）。
3. 理论与实验结果的一致性验证了仿真所依据的数学模型的有效性，同时也证明了所提出的防摆控制方法的有效性。
4. 通过对负载悬挂点速度的控制，可根据动态载荷和响应的要求与限制，在较宽范围内选择瞬态过程的参数。
5. 所提出的控制方法基于形成预定偏转角，该偏转角为分段连续函数，其二阶导数无突变，三阶导数为具有一定变号幅值的矩形脉冲，从而消除了起重机结构和运动齿轮中的机械应力。
6. 所提出的防摆控制方法的显著特点是瞬态过程中力（电机转矩）符号恒定，这使得该方法在现代变频驱动器或直接转矩控制系统中物理上可实现。此外，防摆控制仅需测量绳索长度，其余参数均可从机构额定参数中获取，无需额外测量。
7. 基于启动和制动过程中机构与负载的速度图制定策略，提高了系统安全性，运动平稳性使得起重机可实现自动化操作，包括在预定位置对负载进行精确定位。此类自动化操作可在自动化码头作业的集装箱起重机设计中实施。