70. Climbing Stairs

最新推荐文章于 2024-01-18 13:59:59 发布

原创最新推荐文章于 2024-01-18 13:59:59 发布 · 261 阅读

0 ·

CC 4.0 BY-SA版权

LeetCode题目专栏收录该内容

51 篇文章

订阅专栏

本文探讨了经典的爬楼梯问题，通过动态规划的方法来计算达到顶层的不同方式数量。给出了两种实现方案，一种使用数组记录每一步的结果，另一种则采用更简洁的方式，仅用两个变量迭代计算。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

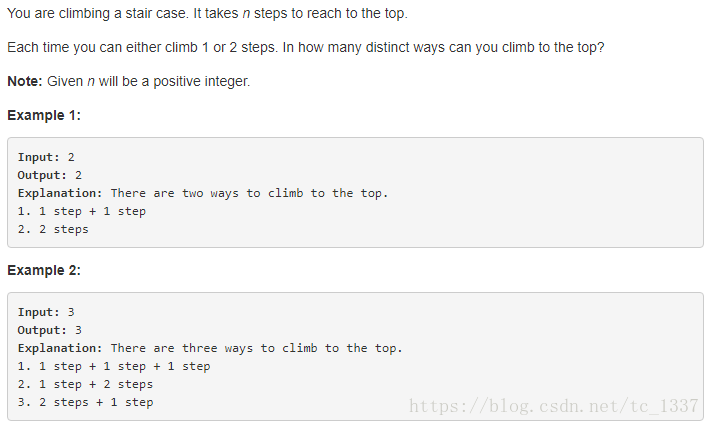
你正在爬楼梯，需要n个步骤才能到达顶部。

每一次你可以爬1步或2步。有多少种不同的方法可以爬到顶端？

注：给定的n为正整数。

1. 动态规划思想

思路：

当n<=1，爬1步

当n>1时，对于第i个台阶，到达该台阶有两种方法，从第i-1个台阶上迈一步，或从第i-2个台阶上迈两步。

即到达台阶i的方法数=到达台阶i-1的方法数+到达台阶i-2的方法数。

 public int climbStairs(int n)
{
	if (n <= 1)
	{
		return 1;
	}
	int[] dp = new int[n];
	dp[0] = 1; // 第一层 1
	dp[1] = 2; // 第二层 1, 2
	for (int i=2; i<n; i++)
	{
		dp[i] = dp[i-1] + dp[i-2];
	}
	return dp[n-1];
}

更加简洁的代码

int climbStairs(int n)
{
	int a = 1;
	int b = 1;
	while (n-- > 0)
	{
		int tmp = a;
		a = b;
		b += tmp;
	}
	return a;
}