HTTPS、TLS

本文转载：

• 小林coding
• 小林coding
• YongApple

一、TLS握手过程

HTTP 由于是明文传输，所谓的明文，就是说客户端与服务端通信的信息都是肉眼可见的，随意使用一个抓包工具都可以截获通信的内容。

所以安全上存在以下三个风险：

窃听风险，比如通信链路上可以获取通信内容，用户号容易没。
篡改风险，比如强制植入垃圾广告，视觉污染，用户眼容易瞎。
冒充风险，比如冒充淘宝网站，用户钱容易没。
HTTPS 在 HTTP 与 TCP 层之间加入了 TLS 协议，来解决上述的风险。

TLS 协议是如何解决 HTTP 的风险的呢？

信息加密： HTTP 交互信息是被加密的，第三方就无法被窃取；
校验机制：校验信息传输过程中是否有被第三方篡改过，如果被篡改过，则会有警告提示；
身份证书：证明淘宝是真的淘宝网；
可见，有了 TLS 协议，能保证 HTTP 通信是安全的了，那么在进行 HTTP 通信前，需要先进行 TLS 握手。TLS 的握手过程，如下图：

上图简要概述来 TLS 的握手过程，其中每一个「框」都是一个记录（record），记录是 TLS 收发数据的基本单位，类似于 TCP 里的 segment。多个记录可以组合成一个 TCP 包发送，所以通常经过「四个消息」就可以完成 TLS 握手，也就是需要 2个 RTT 的时延，然后就可以在安全的通信环境里发送 HTTP 报文，实现 HTTPS 协议。

所以可以发现，HTTPS 是应用层协议，需要先完成 TCP 连接建立，然后走 TLS 握手过程后，才能建立通信安全的连接。

事实上，不同的密钥交换算法，TLS 的握手过程可能会有一些区别。

这里先简单介绍下密钥交换算法，因为考虑到性能的问题，所以双方在加密应用信息时使用的是对称加密密钥，而对称加密密钥是不能被泄漏的，为了保证对称加密密钥的安全性，所以使用非对称加密的方式来保护对称加密密钥的协商，这个工作就是密钥交换算法负责的。

二、RSA握手过程

传统的 TLS 握手基本都是使用 RSA 算法来实现密钥交换的，在将 TLS 证书部署服务端时，证书文件中包含一对公私钥，其中公钥会在 TLS 握手阶段传递给客户端，私钥则一直留在服务端，一定要确保私钥不能被窃取。

在 RSA 密钥协商算法中，客户端会生成随机密钥，并使用服务端的公钥加密后再传给服务端。根据非对称加密算法，公钥加密的消息仅能通过私钥解密，这样服务端解密后，双方就得到了相同的密钥，再用它加密应用消息。

我用 Wireshark 工具抓了用 RSA 密钥交换的 TLS 握手过程，你可以从下面看到，一共经历来四次握手：

对应 Wireshark 的抓包，我也画了一幅图，你可以从下图很清晰地看到该过程：

那么，接下来针对每一个 TLS 握手做进一步的介绍。

TLS 第一次握手

客户端首先会发一个「Client Hello」消息，字面意思我们也能理解到，这是跟服务器「打招呼」。

消息里面有客户端使用的 TLS 版本号、支持的密码套件列表，以及生成的随机数（Client Random），这个随机数会被服务端保留，它是生成对称加密密钥的材料之一。

TLS 第二次握手

当服务端收到客户端的「Client Hello」消息后，会确认 TLS 版本号是否支持，和从密码套件列表中选择一个密码套件，以及生成随机数（Server Random）。

接着，返回「Server Hello」消息，消息里面有服务器确认的 TLS 版本号，也给出了随机数（Server Random），然后从客户端的密码套件列表选择了一个合适的密码套件。

可以看到，服务端选择的密码套件是 “Cipher Suite: TLS_RSA_WITH_AES_128_GCM_SHA256”。

这个密码套件看起来真让人头晕，好一大串，但是其实它是有固定格式和规范的。基本的形式是「密钥交换算法 + 签名算法 + 对称加密算法 + 摘要算法」， 一般 WITH 单词前面有两个单词，第一个单词是约定密钥交换的算法，第二个单词是约定证书的验证算法。比如刚才的密码套件的意思就是：

• 由于 WITH 单词只有一个 RSA，则说明握手时密钥交换算法和签名算法都是使用 RSA；
• 握手后的通信使用 AES 对称算法，密钥长度 128 位，分组模式是 GCM；
• 摘要算法 SHA384 用于消息认证和产生随机数；
• 就前面这两个客户端和服务端相互「打招呼」的过程，客户端和服务端就已确认了 TLS
  版本和使用的密码套件，而且你可能发现客户端和服务端都会各自生成一个随机数，并且还会把随机数传递给对方。

那这个随机数有啥用呢？其实这两个随机数是后续作为生成「会话密钥」的条件，所谓的会话密钥就是数据传输时，所使用的对称加密密钥。

然后，服务端为了证明自己的身份，会发送「Server Certificate」给客户端，这个消息里含有数字证书。

随后，服务端发了「Server Hello Done」消息，目的是告诉客户端，我已经把该给你的东西都给你了，本次打招呼完毕。

TLS 第三次握手

客户端验证完证书后，认为可信则继续往下走。接着，客户端就会生成一个新的随机数 (pre-master)，用服务器的 RSA 公钥加密该随机数，通过「Change Cipher Key Exchange」消息传给服务端。

服务端收到后，用 RSA 私钥解密，得到客户端发来的随机数 (pre-master)。

至此，客户端和服务端双方都共享了三个随机数，分别是 Client Random、Server Random、pre-master。

于是，双方根据已经得到的三个随机数，生成会话密钥（Master Secret），它是对称密钥，用于对后续的 HTTP 请求/响应的数据加解密。

生成完会话密钥后，然后客户端发一个「Change Cipher Spec」，告诉服务端开始使用加密方式发送消息。

然后，客户端再发一个「Encrypted Handshake Message（Finishd）」消息，把之前所有发送的数据做个摘要，再用会话密钥（master secret）加密一下，让服务器做个验证，验证加密通信是否可用和之前握手信息是否有被中途篡改过。

可以发现，「Change Cipher Spec」之前传输的 TLS 握手数据都是明文，之后都是对称密钥加密的密文。

TLS 第四次握手

服务器也是同样的操作，发「Change Cipher Spec」和「Encrypted Handshake Message」消息，如果双方都验证加密和解密没问题，那么握手正式完成。

最后，就用「会话密钥」加解密 HTTP 请求和响应了。

RSA 算法的缺陷

使用 RSA 密钥协商算法的最大问题是不支持前向保密。因为客户端传递随机数（用于生成对称加密密钥的条件之一）给服务端时使用的是公钥加密的，服务端收到到后，会用私钥解密得到随机数。所以一旦服务端的私钥泄漏了，过去被第三方截获的所有 TLS 通讯密文都会被破解。

为了解决这一问题，于是就有了 DH 密钥协商算法，这里简单介绍它的工作流程。

客户端和服务端各自会生成随机数，并以此作为私钥，然后根据公开的 DH 计算公示算出各自的公钥，通过 TLS 握手双方交换各自的公钥，这样双方都有自己的私钥和对方的公钥，然后双方根据各自持有的材料算出一个随机数，这个随机数的值双方都是一样的，这就可以作为后续对称加密时使用的密钥。

DH 密钥交换过程中，即使第三方截获了 TLS 握手阶段传递的公钥，在不知道的私钥的情况下，也是无法计算出密钥的，而且每一次对称加密密钥都是实时生成的，实现前向保密。

但因为 DH 算法的计算效率问题，后面出现了 ECDHE 密钥协商算法，我们现在大多数网站使用的正是 ECDHE 密钥协商算法。

三、ECDHE密匙交换算法及握手过程

离散对数

ECDHE 密钥协商算法是 DH 算法演进过来的，所以我们先从 DH 算法说起。

DH 算法是非对称加密算法， 因此它可以用于密钥交换，该算法的核心数学思想是离散对数。

是不是听到这个数学概念就怂了？不怕，这次不会说离散对数推到的过程，只简单提一下它的数学公式。

离散对数是「离散 + 对数」的两个数学概念的组合，所以我们先来复习一遍对数。

要说起对数，必然要说指数，因为它们是互为反函数，指数就是幂运算，对数是指数的逆运算。

举个栗子，如果以 2 作为底数，那么指数和对数运算公式，如下图所示：

那么对于底数为 2 的时候， 32 的对数是 5，64 的对数是 6，计算过程如下：

对数运算的取值是可以连续的，而离散对数的取值是不能连续的，因此也以「离散」得名，

离散对数是在对数运算的基础上加了「模运算」，也就说取余数，对应编程语言的操作符是「%」，也可以用 mod 表示。离散对数的概念如下图：

上图的，底数 a 和模数 p 是离散对数的公共参数，也就说是公开的，b 是真数，i 是对数。知道了对数，就可以用上面的公式计算出真数。但反过来，知道真数却很难推算出对数。

特别是当模数 p 是一个很大的质数，即使知道底数 a 和真数 b ，在现有的计算机的计算水平是几乎无法算出离散对数的，这就是 DH 算法的数学基础。

DH算法

认识了离散对数，我们来看看 DH 算法是如何密钥交换的。

现假设小红和小明约定使用 DH 算法来交换密钥，那么基于离散对数，小红和小明需要先确定模数和底数作为算法的参数，这两个参数是公开的，用 P 和 G 来代称。

然后小红和小明各自生成一个随机整数作为私钥，双方的私钥要各自严格保管，不能泄漏，小红的私钥用 a 代称，小明的私钥用 b 代称。

现在小红和小明双方都有了 P 和 G 以及各自的私钥，于是就可以计算出公钥：

• 小红的公钥记作 A，A = G ^ a ( mod P )；
• 小明的公钥记作 B，B = G ^ b ( mod P )；

A 和 B 也是公开的，因为根据离散对数的原理，从真数（A 和 B）反向计算对数 a 和 b 是非常困难的，至少在现有计算机的计算能力是无法破解的，如果量子计算机出来了，那就有可能被破解，当然如果量子计算机真的出来了，那么密钥协商算法就要做大的升级了。

双方交换各自 DH 公钥后，小红手上共有 5 个数：P、G、a、A、B，小明手上也同样共有 5 个数：P、G、b、B、A。

然后小红执行运算： B ^ a ( mod P )，其结果为 K，因为离散对数的幂运算有交换律，所以小明执行运算： A ^ b ( mod P )，得到的结果也是 K。

这个 K 就是小红和小明之间用的对称加密密钥，可以作为会话密钥使用。

可以看到，整个密钥协商过程中，小红和小明公开了 4 个信息：P、G、A、B，其中 P、G 是算法的参数，A 和 B 是公钥，而 a、b 是双方各自保管的私钥，黑客无法获取这 2 个私钥，因此黑客只能从公开的 P、G、A、B 入手，计算出离散对数（私钥）。

前面也多次强调， 根据离散对数的原理，如果 P 是一个大数，在现有的计算机的计算能力是很难破解出 私钥 a、b 的，破解不出私钥，也就无法计算出会话密钥，因此 DH 密钥交换是安全的。

DHE算法

根据私钥生成的方式，DH 算法分为两种实现：

• static DH 算法，这个是已经被废弃了；
• DHE 算法，现在常用的；

static DH 算法里有一方的私钥是静态的，也就说每次密钥协商的时候有一方的私钥都是一样的，一般是服务器方固定，即 a 不变，客户端的私钥则是随机生成的。

于是，DH 交换密钥时就只有客户端的公钥是变化，而服务端公钥是不变的，那么随着时间延长，黑客就会截获海量的密钥协商过程的数据，因为密钥协商的过程有些数据是公开的，黑客就可以依据这些数据暴力破解出服务器的私钥，然后就可以计算出会话密钥了，于是之前截获的加密数据会被破解，所以 static DH 算法不具备前向安全性。

既然固定一方的私钥有被破解的风险，那么干脆就让双方的私钥在每次密钥交换通信时，都是随机生成的、临时的，这个方式也就是 DHE 算法，E 全称是 ephemeral（临时性的）。

所以，即使有个牛逼的黑客破解了某一次通信过程的私钥，其他通信过程的私钥仍然是安全的，因为每个通信过程的私钥都是没有任何关系的，都是独立的，这样就保证了「前向安全」。

ECDHE 算法

DHE 算法由于计算性能不佳，因为需要做大量的乘法，为了提升 DHE 算法的性能，所以就出现了现在广泛用于密钥交换算法 —— ECDHE 算法。

ECDHE 算法是在 DHE 算法的基础上利用了 ECC 椭圆曲线特性，可以用更少的计算量计算出公钥，以及最终的会话密钥。

小红和小明使用 ECDHE 密钥交换算法的过程：

• 双方事先确定好使用哪种椭圆曲线，和曲线上的基点 G，这两个参数都是公开的；
• 双方各自随机生成一个随机数作为私钥d，并与基点 G相乘得到公钥Q（Q = dG），此时小红的公私钥为 Q1 和 d1，小明的公私钥为 Q2
  和 d2；
• 双方交换各自的公钥，最后小红计算点（x1，y1） = d1Q2，小明计算点（x2，y2） =
  d2Q1，由于椭圆曲线上是可以满足乘法交换和结合律，所以 d1Q2 = d1d2G = d2d1G = d2Q1 ，因此双方的 x坐标是一样的，所以它是共享密钥，也就是会话密钥。

这个过程中，双方的私钥都是随机、临时生成的，都是不公开的，即使根据公开的信息（椭圆曲线、公钥、基点 G）也是很难计算出椭圆曲线上的离散对数（私钥）。

ECDHE 握手过程

知道了 ECDHE 算法基本原理后，我们就结合实际的情况来看看。

我用 Wireshark 工具抓了用 ECDHE 密钥协商算法的 TSL 握手过程，可以看到是四次握手：

细心的小伙伴应该发现了，使用了 ECDHE，在 TLS 第四次握手前，客户端就已经发送了加密的 HTTP 数据，而对于 RSA 握手过程，必须要完成 TLS 四次握手，才能传输应用数据。

所以，ECDHE 相比 RSA 握手过程省去了一个消息往返的时间，这个有点「抢跑」的意思，它被称为是「TLS False Start」，跟「TCP Fast Open」有点像，都是在还没连接完全建立前，就发送了应用数据，这样便提高了传输的效率。

接下来，分析每一个 ECDHE 握手过程。

TLS 第一次握手

客户端首先会发一个「Client Hello」消息，消息里面有客户端使用的 TLS 版本号、支持的密码套件列表，以及生成的随机数（Client Random）。

TLS 第二次握手

服务端收到客户端的「打招呼」，同样也要回礼，会返回「Server Hello」消息，消息面有服务器确认的 TLS 版本号，也给出了一个随机数（Server Random），然后从客户端的密码套件列表选择了一个合适的密码套件。

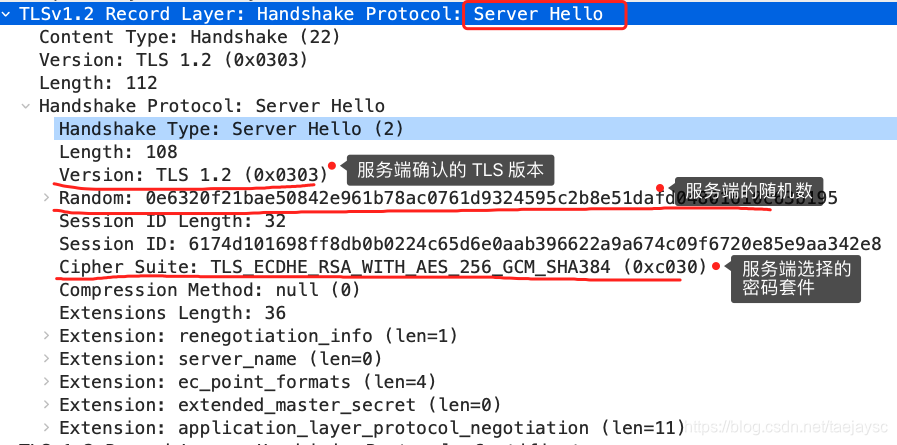
不过，这次选择的密码套件就和 RSA 不一样了，我们来分析一下这次的密码套件的意思。

「 TLS_ECDHE_RSA_WITH_AES_256_GCM_SHA384」

• 密钥协商算法使用 ECDHE；
• 签名算法使用 RSA；
• 握手后的通信使用 AES 对称算法，密钥长度 256 位，分组模式是 GCM；
• 摘要算法使用 SHA384；

接着，服务端为了证明自己的身份，发送「Certificate」消息，会把证书也发给客户端。

这一步就和 RSA 握手过程有很大到区别了，因为服务端选择了 ECDHE 密钥协商算法，所以会在发送完证书后，发送「Server Key Exchange」消息。

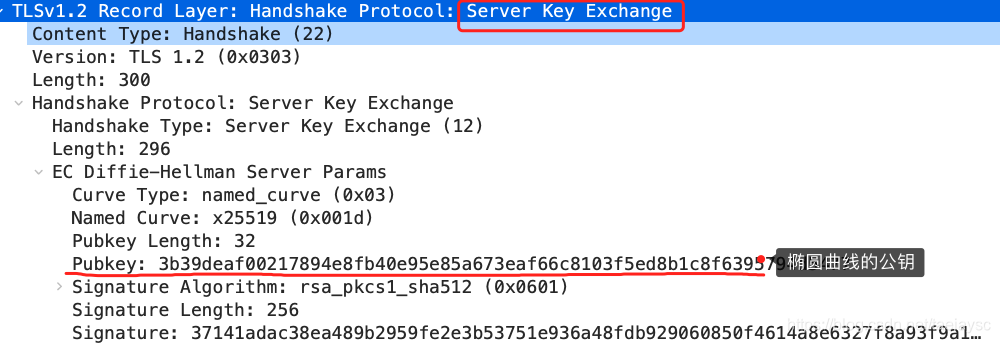
这个过程服务器做了三件事：

• 选择了名为 named_curve 的椭圆曲线，选好了椭圆曲线相当于椭圆曲线基点 G 也定好了，这些都会公开给客户端；
• 生成随机数作为服务端椭圆曲线的私钥，保留到本地；
• 根据基点 G 和私钥计算出服务端的椭圆曲线公钥，这个会公开给客户端。

为了保证这个椭圆曲线的公钥不被第三方篡改，服务端会用 RSA 签名算法给服务端的椭圆曲线公钥做个签名。

随后，就是「Server Hello Done」消息，服务端跟客户端表明：“这些就是我提供的信息，打招呼完毕”。

至此，TLS 两次握手就已经完成了，目前客户端和服务端通过明文共享了这几个信息：Client Random、Server Random 、使用的椭圆曲线、椭圆曲线基点 G、服务端椭圆曲线的公钥，这几个信息很重要，是后续生成会话密钥的材料。

TLS 第三次握手
客户端收到了服务端的证书后，自然要校验证书是否合法，如果证书合法，那么服务端到身份就是没问题的。校验证书到过程，会走证书链逐级验证，确认证书的真实性，再用证书的公钥验证签名，这样就能确认服务端的身份了，确认无误后，就可以继续往下走。

客户端会生成一个随机数作为客户端椭圆曲线的私钥，然后再根据服务端前面给的信息，生成客户端的椭圆曲线公钥，然后用「Client Key Exchange」消息发给服务端。

至此，双方都有对方的椭圆曲线公钥、自己的椭圆曲线私钥、椭圆曲线基点 G。于是，双方都就计算出点（x，y），其中 x 坐标值双方都是一样的，前面说 ECDHE 算法时候，说 x 是会话密钥，但实际应用中，x 还不是最终的会话密钥。

还记得 TLS 握手阶段，客户端和服务端都会生成了一个随机数传递给对方吗？

最终的会话密钥，就是用「客户端随机数 + 服务端随机数 + x（ECDHE 算法算出的共享密钥） 」三个材料生成的。

之所以这么麻烦，是因为 TLS 设计者不信任客户端或服务器「伪随机数」的可靠性，为了保证真正的完全随机，把三个不可靠的随机数混合起来，那么「随机」的程度就非常高了，足够让黑客计算出最终的会话密钥，安全性更高。

算好会话密钥后，客户端会发一个「Change Cipher Spec」消息，告诉服务端后续改用对称算法加密通信。

接着，客户端会发「Encrypted Handshake Message」消息，把之前发送的数据做一个摘要，再用对称密钥加密一下，让服务端做个验证，验证下本次生成的对称密钥是否可以正常使用。

TLS 第四次握手

最后，服务端也会有一个同样的操作，发「Change Cipher Spec」和「Encrypted Handshake Message」消息，如果双方都验证加密和解密没问题，那么握手正式完成。于是，就可以正常收发加密的 HTTP 请求和响应了。

RSA 和 ECDHE 握手过程的区别

RSA 和 ECDHE 握手过程的区别：

• RSA 密钥协商算法「不支持」前向保密，ECDHE 密钥协商算法「支持」前向保密；
• 使用了 RSA 密钥协商算法，TLS 完成四次握手后，才能进行应用数据传输，而对于 ECDHE 算法，客户端可以不用等服务端的最后一次
  TLS 握手，就可以提前发出加密的 HTTP 数据，节省了一个消息的往返时间；
• 使用 ECDHE， 在 TLS 第 2 次握手中，会出现服务器端发出的「Server Key Exchange」消息，而 RSA
  握手过程没有该消息；

密匙交换算法及其原理

密钥交换/协商机制要达到啥目的？

前一篇介绍了 SSL/TLS 的身份认证机制。这个机制是为了防止攻击者通过【篡改】网络传输数据，来假冒身份，以达到“中间人攻击/MITM”的目的。
　　
而今天要聊的“密钥协商机制”是：（在身份认证的前提下）如何规避【偷窥】的风险。

通俗地说，即使有攻击者在偷窥你与服务器的网络传输，客户端（client）依然可以利用“密钥协商机制”与服务器端（server）协商出一个用来加密应用层数据的密钥（也称“会话密钥”）。

密钥交换/协商机制的几种类型

俺总结了一下，大致有如下几种类型：

依靠非对称加密算法

原理：

拿到公钥的一方先生成随机的会话密钥，然后利用公钥加密它；再把加密结果发给对方，对方用私钥解密；于是双方都得到了会话密钥。

举例：
　　RSA

依靠专门的密钥交换算法

原理：
　　这个原理比较复杂，一两句话说不清楚，待会儿聊到 DH 的那个章节会详谈。

举例：
　　DH 算法及其变种

依靠通讯双方事先已经共享的“秘密”

原理：
　　既然双方已经有共享的秘密（这个“秘密”可能已经是一个密钥，也可能只是某个密码/password），只需要根据某种生成算法，就可以让双方产生相同的密钥（并且密钥长度可以任意指定）

举例：
　　PSK 和 SRP（可能很多同学没听过这俩玩意儿。别担心，本文后续部分有介绍）

基于 RSA 的密钥协商

概述

这大概是 SSL 最古老的密钥协商方式——早期的 SSLv2 只支持一种密钥协商机制，就是它。（前一篇）介绍身份认证重要性的时候，也是拿 RSA 来演示。
　　
RSA 是一种【非】对称加密算法。在本系列第1篇的背景知识介绍中，已经聊过这种算法的特点——加密和解密用使用【不同的】密钥。并且“非对称加密算法”既可以用来做“加密/解密”，还可以用来做“数字签名”。

密钥协商的步骤

（下列步骤只阐述原理，具体的协议细节在下一篇讲）

1. 客户端连上服务端
2. 服务端发送 CA 证书给客户端
3. 客户端验证该证书的可靠性
4. 客户端从 CA 证书中取出公钥
5. 客户端生成一个随机密钥 k，并用这个公钥加密得到 k’
6. 客户端把 k’ 发送给服务端
7. 服务端收到 k’ 后用自己的私钥解密得到 k
8. 此时双方都得到了密钥 k，协商完成。

如何防范偷窥（嗅探）

• 攻击方式1

攻击者虽然可以监视网络流量并拿到公钥，但是【无法】通过公钥推算出私钥（这点由 RSA 算法保证）

• 攻击方式2

攻击者虽然可以监视网络流量并拿到 k’，但是攻击者没有私钥，【无法解密】 k’，因此也就无法得到 k

如何防范篡改（假冒身份）

• 攻击方式1

如果攻击者在第2步篡改数据，伪造了证书，那么客户端在第3步会发现（这点由证书体系保证）

• 攻击方式2

如果攻击者在第6步篡改数据，伪造了k’，那么服务端收到假的k’之后，解密会失败（这点由 RSA 算法保证）。服务端就知道被攻击了。

基于 DH 的密钥协商

概述

DH 算法又称“Diffie–Hellman 算法”。这是两位数学牛人的名称，他们创立了这个算法。该算法用来实现【安全的】“密钥交换”。它可以做到——“通讯双方在完全没有对方任何预先信息的条件下通过不安全信道创建起一个密钥”。这句话比较绕口，通俗地说，可以归结为两个优点：

• 通讯双方事先【不】需要有共享的秘密。
• 用该算法协商密码，即使协商过程中被别人全程偷窥（比如“网络嗅探”），偷窥者也【无法】知道协商得出的密钥是啥。

但是 DH 算法本身也有缺点——它不支持认证。也就是说：它虽然可以对抗“偷窥”，却无法对抗“篡改”，自然也就无法对抗“中间人攻击/MITM”（在本系列的前一篇，俺已经强调过了——缺乏身份认证，【必定会】遭到“中间人攻击/MITM”）。
　　
　　为了避免遭遇 MITM 攻击，DH 需要与其它签名算法（比如 RSA、DSA、ECDSA）配合——靠签名算法帮忙来进行身份认证。当 DH 与 RSA 配合使用，称之为“DH-RSA”，与 DSA 配合则称为“DH-DSA”，以此类推。
　　
　　反之，如果 DH 【没有】配合某种签名算法，则称为“DH-ANON”（ANON 是洋文“匿名”的简写）。此时会遭遇“中间人攻击/MITM”。（具体的中间人攻击手法，可以参见本系列前一篇）

关于该算法的更多介绍，可以参见维基百科（这个条目）。

数学原理

（如果你属于那种“看了数学公式就犯晕的人”，可以直接略过本小节，不影响你看后续的章节）

从概念上讲：DH 依赖的是：求解“离散对数问题”的复杂性。具体的算法如下：

• 通讯双方（张三、李四）需要先约定好算法参数（algorithm parameters）：一个素数 p 作为模数，一个素数 g 作为基数（g 也称为“生成元”）。这两个算法参数是可以对外公开滴。

• 对于张三而言，需要先想好一个秘密的自然数 a 作为私钥（不能公开），然后计算 A = ga mod p 作为自己的公钥（可以公开）。

• 对李四而言也类似，先想好一个秘密的自然数 b 作为私钥（不能公开），然后计算 B = gb mod p 作为自己的公钥（可以公开）。

• 张三和李四互相交换各自的公钥。

• 然后张三计算出 k = Ba mod p，李四计算出 k = Ab mod p

该算法至少确保了如下几点：

1. 张三和李四分别计算出来的 k 必定是一致的
2. 张三和李四都无法根据已知的数来推算出对方的私钥（张三无法推算出 b，李四无法推算出 a）
3. 对于一个旁观者（偷窥者），虽然能看到 p，g，A，B，但是无法推算出 a 和 b（就是说，旁观者无法推算出双方的私钥），自然也无法推算出 k

举例
　　
　　前面说得都是符号，比较抽象。下面拿具体数字举例：
假设约定的算法参数：模数是 97，基数是 3
张三用的私钥是 6，李四用的私钥是 21，用 python 代码演示如下（python 语言用两个连续星号表示“幂运算”，用百分号表示“取模运算”）：

p = 97
g = 3

a = 6
b = 21

A = (g**a) % p
B = (g**b) % p

print((B**a) % p) # 47
print((A**b) % p) # 47

最后打印出来的两个 47 就是双方都计算出了【相同的】结果（这个数值可以用作之后的“会话密钥”）

上面因为是举例，用的数字都比较小。在实战中需要注意如下几点，以降低被攻击的风险。

1. p 必须是质数且足够大（至少300位）
2. a，b 也要足够大（至少100位），且必须是随机生成。
3. g 必须是质数，【不】需要很大，比如 2 或 3 或 5 都可以。g 如果太大并【不能】显著提升安全性，反而会影响性能。

密钥协商的步骤

（下列步骤只阐述原理，具体的协议细节在下一篇讲）

1. 客户端先连上服务端
2. 服务端生成一个随机数 s 作为自己的私钥，然后根据算法参数计算出公钥 S（算法参数通常是固定的）
3. 服务端使用某种签名算法把“算法参数（模数p，基数g）和服务端公钥S”作为一个整体进行签名
4. 服务端把“算法参数（模数p，基数g）、服务端公钥S、签名”发送给客户端
5. 客户端收到后验证签名是否有效
6. 客户端生成一个随机数 c 作为自己的私钥，然后根据算法参数计算出公钥 C
7. 客户端把 C 发送给服务端
8. 客户端和服务端（根据上述 DH 算法）各自计算出 k 作为会话密钥

如何防范偷窥（嗅探）

嗅探者可以通过监视网络传输，得到算法参数（模数p，基数g）以及双方的公钥，但是【无法】推算出双方的私钥，也【无法】推算出会话密钥（这是由 DH 算法在数学上保证的）

如何防范篡改（假冒身份）

• 攻击方式1

攻击者可以第4步篡改数据（修改算法参数或服务端公钥）。但因为这些信息已经进行过数字签名。篡改之后会被客户端发现。

• 攻击方式2

攻击者可以在第7步篡改客户端公钥。这步没有签名，服务端收到数据后不会发现被篡改。但是，攻击者篡改之后会导致“服务端与客户端生成的会话密钥【不一致】”。在后续的通讯步骤中会发现这点，并导致通讯终止。
　　（下一篇讲具体协议的时候会提到：协议初始化/握手阶段的末尾，双方都会向对方发送一段“验证性的密文”，这段密文用各自的会话密钥进行【对称】加密，如果双方的会话密钥不一致，这一步就会失败，进而导致握手失败，连接终止）

DH 的变种

基于“椭圆曲线”的 ECDH

DH 算法有一个变种，称之为 ECDH（全称是“Elliptic Curve Diffie-Hellman”）。维基条目在“这里”
　　它与 DH 类似，差别在于：

• DH 依赖的是——求解“离散对数问题”的困难。
• ECDH 依赖的是——求解“椭圆曲线离散对数问题”的困难。

ECDH 的数学原理比 DH 更复杂。考虑到本文读者大都【不是】数学系出身，俺就不展开了。

ECDH 跟 DH 一样，也是【无认证】的。同样需要跟其它签名算法（比如 RSA、DSA、ECDSA）配合。

对 DH 和 ECDH 进行“临时密钥”的改良——DHE 和 ECDHE

刚才介绍的 DH 和 ECDH，其密钥是持久的（静态的）。也就是说，通讯双方生成各自的密钥之后，就长时间用下去。这么干当然比较省事儿（节约性能），但是存在某种安全隐患——无法做到“前向保密”（洋文是“forward secrecy”）。
　　
　　为了做到“前向保密”，采用“临时密钥”（洋文是“ephemeral key”）的方式对 DH 和 ECDH 进行改良。于是得到两种新的算法——DHE 和 ECDHE。（这两种新算法的名称，就是在原有名称后面加上字母 E 表示 ephemeral）。其实算法还是一样的，只是对每个会话都要重新协商一次密钥，且密钥用完就丢弃。
　　
　　（估计很多同学不太了解“前向保密”这个概念。俺会在本系列中单独开一帖，介绍“前向保密”的概念及其好处）

基于 PSK 的密钥协商

概述

PSK 是洋文“Pre-Shared Key”的缩写。顾名思义，就是【预先】让通讯双方共享一些密钥（通常是【对称加密】的密钥）。所谓的【预先】，就是说，这些密钥在 TLS 连接尚未建立之前，就已经部署在通讯双方的系统内了。
　　
　　这种算法用的不多，它的好处是：

1. 不需要依赖公钥体系，不需要部属 CA 证书。
2. 不需要涉及非对称加密，TLS 协议握手（初始化）时的性能好于前述的 RSA 和 DH。
   　　更多介绍可以参见维基百科，链接在“这里”。

密钥协商的步骤

（由于 PSK 用的不多，下面只简单介绍一下步骤，让大伙儿明白其原理）

• 在通讯【之前】，通讯双方已经预先部署了若干个共享的密钥。
• 为了标识多个密钥，给每一个密钥定义一个唯一的 ID
• 协商的过程很简单：客户端把自己选好的密钥的 ID 告诉服务端。
• 如果服务端在自己的密钥池子中找到这个 ID，就用对应的密钥与客户端通讯；否则就报错并中断连接。

如何防范偷窥（嗅探）

使用这种算法，在协商密钥的过程中交换的是密钥的标识（ID）而【不是】密钥本身。
　　
就算攻击者监视了全过程，也无法知晓密钥啥。

如何防范篡改（假冒身份）

PSK 可以单独使用，也可以搭配签名算法一起使用。

对于单独使用
　　
　　如果攻击者篡改了协商过程中传送的密钥 ID，要么服务端发现 ID 无效（协商失败），要么服务端得到的 ID 与客户端不一致，在后续的通讯步骤中也会发现，并导致通讯终止。
　　
　　（下一篇讲具体协议的时候会提到：协议初始化/握手阶段的末尾，双方都会向对方发送一段“验证性的密文”，这段密文用各自的会话密钥进行【对称】加密，如果双方的会话密钥不一致，这一步就会失败，进而导致握手失败，连接终止）

对于搭配签名算法
　　
　　如果攻击者篡改了协商过程中传送的密钥 ID，验证签名会失败

补充说明

PSK 与 RSA 具有某种相似性——既可以用来搞“密钥协商”，也可以用来搞“身份认证”。
　　所以，PSK 可以跟 DH（及其变种）进行组合。例如：DHE-PSK、ECDHE-PSK
　　关于 PSK 的更多细节，可以参见 RFC4279

基于 SRP 的密钥协商

概述

SRP 是洋文“Secure Remote Password”的缩写。这个算法有点类似于刚才提到的 PSK——只不过 client/server 双方共享的是比较人性化的密码（password）而不是密钥（key）。该算法采用了一些机制（盐/salt、随机数）来防范“嗅探/sniffer”或“字典猜解攻击”或“重放攻击”。
　　
　　这个算法应该用得很少——OpenSSL 直到2012年才开始支持该算法。所以俺这里就不展开了。有兴趣的同学可以去看 RFC2945 的协议描述。

密钥协商的步骤

（由于 SRP 用的不多，俺偷懒一下，略去此小节）

各种组合的一览表

算法组合	密钥交换	身份认证	是否会遭遇 中间人攻击	是否具备 前向保密	SSL 2.0	SSL 3.0	TLS 1.0	TLS 1.1	TLS 1.2	TLS 1.3 （草案）
RSA	RSA	RSA	否	否	是	是	是	是	是	否
DH-RSA	DH	RSA	否	否	否	是	是	是	是	否
DH-DSA	DH	DSA	否	否	否	是	是	是	是	否
DHE-RSA	DHE	RSA	否	是	否	是	是	是	是	是
DHE-DSA	DHE	DSA	否	是	否	是	是	是	是	是
ECDH-RSA	ECDH	RSA	否	否	否	否	是	是	是	否
ECDH-ECDSA	ECDH	ECDSA	否	否	否	否	是	是	是	否
ECDHE-RSA	DHE	RSA	否	是	否	否	是	是	是	是
ECDHE-ECDSA	DHE	ECDSA	否	是	否	否	是	是	是	是
PSK	PSK	PSK	否	否	否	否	是	是	是	？
PSK-RSA	PSK	RSA	否	否	否	否	是	是	是	？
DHE-PSK	DHE	PSK	否	是	否	否	是	是	是	？
ECDHE-PSK	DHE	PSK	否	是	否	否	是	是	是	？
SRP	SRP	SRP	否	否	否	否	是	是	是	？
SRP-RSA	SRP	RSA	否	否	否	否	是	是	是	？
SRP-DSA	SRP	DSA	否	否	否	否	是	是	是	？
DH-ANON	DH	无	是	否	否	是	是	是	是	否
ECDH-ANON	ECDH	无	是	否	否	否	是	是	是	否