汽车啁啾序列雷达干扰分析

汽车啁啾序列雷达的对等干扰分析

摘要

由于配备此类系统的车辆迅速增加，汽车雷达传感器之间的相互干扰正成为一个主要问题。尽管关于调频连续波（FMCW）雷达的干扰已有大量研究，但在汽车领域日益流行的啁啾序列（CS）雷达方面，文献中尚未见相关报道。为此，本文对汽车啁啾序列（CS）雷达的相互干扰进行了研究。我们通过解析方法推导出描述虚警目标出现概率以及信号对干扰抑制增益的公式，涵盖了连续波、FMCW和CS波形之间的干扰，并与等效FMCW雷达模型进行了比较。所推导的信号对干扰抑制增益公式也通过仿真结果得到了验证。

索引词 —汽车雷达，干扰，啁啾序列，FMCW。

I. 引言

RECENTLY，汽车雷达传感器已成为各种舒适性和安全功能（如自适应巡航控制和自动紧急制动）的关键组件。其快速的市场渗透引发了对汽车雷达之间相互干扰风险的严重关注。已有大量文献针对这一问题进行了分析[1]–[6]，（主要集中在频率调制连续波（FMCW）雷达），FMCW雷达由于硬件和处理需求相对简单，已在汽车领域得到最广泛的应用。

尽管模拟和数字域的硬件复杂度显著更高，但由于啁啾序列（CS）雷达具有无模糊地分辨距离和速度的固有能力，其正受到越来越多的青睐。这不仅消除了调频连续波雷达在多个线性调频信号之间进行易产生虚警的关联任务[7],[8]，还有助于从强静止杂波中检测目标。缩短周期时间是另一项优势（见第二节-C）。

第二部分 系统模型

A. CS雷达工作原理

参考图2，发射信号（或图1中压控振荡器的输出信号）的瞬时频率可以表示为

$$
f_T(t) = f_c + \alpha r_t, \quad (1)
$$

其中 $ f_c $ 是载波频率，$ \alpha $ 是啁啾斜率，$ r_t $ 是从每个线性调频脉冲开始处测量的时间偏移。啁啾斜率定义为 $ \alpha = \frac{BW_{sw}}{T_{cp}} $，其中 $ BW_{sw} $ 和 $ T_{cp} $ 分别为啁啾扫频带宽和啁啾持续时间。注意，$ r_t $ 可以表示为 $ r_t = t - q_t T_{cp} $，其中 $ q_t = \left\lfloor \frac{t}{T_{cp}} \right\rfloor $ 是当前时间 $ t $ 对应的啁啾编号。发射信号的相位可表示为

$$
\varphi_T(t) = 2\pi \int_0^t f_T(\zeta) d\zeta = 2\pi f_c t + 2\pi \alpha \int_0^t r_\zeta d\zeta
= 2\pi f_c t + \pi \alpha T_{cp}^2 q_t + \pi \alpha r_t^2. \quad (2)
$$

接收信号的相位为 $ \varphi_R(t) = \varphi_T(t - \tau) $，其中 $ \tau $ 是雷达与目标之间的双向传播延迟，该信号通过发射信号（利用图1中的混频器）进行去啁啾，从而得到差频信号，其相位为

$$
\varphi_B(t) = \varphi_T(t) - \varphi_R(t) = \varphi_T(t) - \varphi_T(t - \tau)
= 2\pi f_c \tau + \pi \alpha T_{cp}^2 (q_t - q_{t-\tau}) + \pi \alpha (r_t^2 - r_{t-\tau}^2). \quad (3)
$$

通过仅对 $ r_t \geq \tau_{\text{max}} \geq \tau $ 处的差频信号进行处理，其中 $ \tau_{\text{max}} $ 对应于位于关注的最大距离处的目标，我们得到

$$
q_{t-\tau} = q_t,
$$
$$
r_{t-\tau} = t - \tau - q_{t-\tau} T_{cp} = r_t - \tau,
\quad (4)
$$

因此

$$
\varphi_B(t) = 2\pi f_c \tau + 2\pi \alpha \tau r_t - \pi \alpha \tau^2. \quad (5)
$$

对于距离为 $ R = R_0 + vt $ 的目标，其中 $ R_0 $ 和 $ v $ 分别为目标的初始距离和相对径向速度，传播延迟表示为

$$
\tau = \frac{2R}{c} = \tau_0 + \frac{2v}{c} t
= \tau_0 + \frac{2v}{c} T_{cp} q_t + \frac{2v}{c} r_t, \quad (6)
$$

其中 $ \tau_0 = 2R_0 / c $，$ c $ 表示光速。对于典型的汽车雷达参数，(5)中的第二项相对于第一项是平滑的，第三项可忽略，因此可得到 $ \varphi_B(t) $ 的近似

$$
\varphi_B(t) \approx 2\pi f_c \tau + 2\pi \alpha \tau_0 r_t = 2\pi f_c \tau_0 + 2\pi(f_R + f_D)r_t + 2\pi f_D T_{cp} q_t, \quad (7)
$$

表I 汽车调频连续波雷达典型参数
$ f_c $
77 GHz

其中

$$
f_R = \alpha \tau_0 \approx \frac{\alpha 2R}{c}, \quad (8)
$$
$$
f_D = \frac{2v}{c} f_c = \frac{2v}{\lambda}. \quad (9)
$$

差频信号在包含 $ N_{cp} $ 个线性调频信号的相干处理间隔（CPI）内被采集，因此CPI的持续时间为

$$
T_{\text{CPI}} = N_{cp} T_{cp}. \quad (10)
$$

将差频信号按 $ r_t $ 和 $ q_t $ 排列成二维形式，以采样周期 $ T_s $ 进行采样，使得 $ r_t = nT_s $，并令 $ q_t = k $，则(7)可重写为

$$
\varphi_B[n, k] = 2\pi f_c \tau_0 + 2\pi(f_R + f_D)T_s n + 2\pi f_D T_{cp} k. \quad (11)
$$

变量 $ n $ 和 $ k $ 分别称为快时间和慢时间。从上述表达式可以看出，对差频信号进行二维离散傅里叶变换(DFT)后，在频谱中会在对应于快时间和慢时间频率 $ f_R + f_D $ 和 $ f_D $ 的位置产生一个峰值。对于CS汽车雷达，通常情况下 $ f_R \gg f_D $，因此可以忽略 $ f_D $ 对观测到的快时间频率的贡献。一旦在频谱中检测到目标峰值，便可根据 $ f_R $ 和 $ f_D $ 计算出对应的目标距离和速度。注意，一个完整的测量周期包含一个相干处理间隔(CPI)，即周期时间长度为

$$
T_{\text{cyc}} = T_{\text{CPI}}. \quad (12)
$$

压缩感知雷达测量的距离分辨率 $ \Delta R $ 和速度分辨率 $ \Delta v $ 分别通过(8)和(9)与快时间频率分辨率 $ \Delta f_R $ 和慢时间频率分辨率 $ \Delta f_D $ 相关，而每个频率分辨率由其对应的观测时间决定：

$$
\Delta R = \frac{c}{2\alpha} \Delta f_R = \frac{c}{2\alpha} \cdot \frac{1}{T_{cp}} = \frac{c}{2BW_{sw}}, \quad (13)
$$
$$
\Delta v = \frac{\lambda}{2} \Delta f_D = \frac{\lambda}{2} \cdot \frac{1}{T_{\text{CPI}}}. \quad (14)
$$

表I 表示汽车CS雷达的典型波形和系统参数。对应的距离和速度分辨率（$ \Delta R $ 和 $ \Delta v $）分别为1米和3.6千米/小时[17]。采样频率 $ f_s = 1/T_s $ 根据奈奎斯特采样准则和式(8)选择，以无模糊地检测最大距离（$ R_{\text{max}} $）为208米以内的目标。

$$
f_s = 2f_{R,\text{max}} = \frac{4\alpha R_{\text{max}}}{c}. \quad (15)
$$

B. 仿真平台

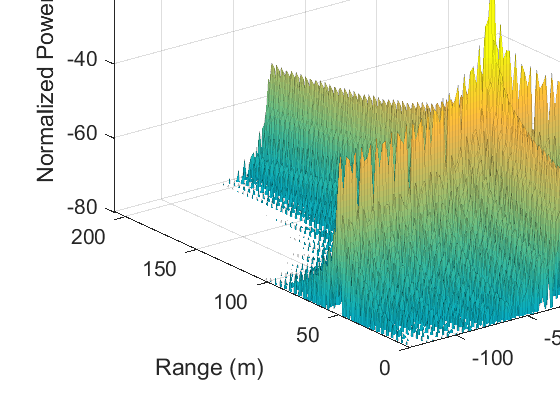
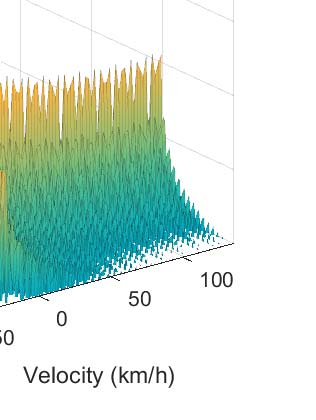
为了验证我们的分析，我们基于表I中的波形和系统参数展示了多种仿真结果。参考图1，模拟前端中的基带波形在采样率 $ 8 \times BW_{sw} $ 下进行仿真，抗混叠滤波器（AAF）使用脉冲不变法[18]建模为八阶巴特沃斯低通滤波器。在数字信号处理（DSP）中，执行512×128离散傅里叶变换并采用零填充以获得距离-速度谱。在我们的仿真中，DFT前未加窗，以便更易于与解析计算进行比较。仿真中未包含噪声，以清晰地展示干扰在受害者频谱中的影响。信号功率已归一化，使得目标信号情况下的峰值为0 dB，如图3a所示。2请注意，仅显示正距离的距离-速度谱，因为负距离对应的频谱可以忽略。尽管我们的仿真结果与分析吻合良好，但需要指出的是，主要的仿真误差源包括非理想抗混叠滤波器和跨bin损耗[19]。具体而言，非理想抗混叠滤波器在高频处产生混叠，导致仿真得到的干扰电平略高；参考目标峰值的跨bin损耗使归一化效果减弱，因此也导致仿真干扰功率略有增加。

距离-速度谱。)
归一化功率（dB）的色谱图)

C. 等效FMCW雷达模型

调频连续波雷达仅使用快时间频率来测量距离和速度。特别是，采用持续时间长得多的线性调频信号，使得 $ f_D $ 在观测到的快时间频率中变得显著。此外，未利用慢时间维，$ f_R $ 和 $ f_D $ 均由单个线性调频脉冲对应的快时间频率测量确定。通过单个线性调频脉冲测量对 $ f_R $ 和 $ f_D $ 产生的模糊问题，

可以在距离-速度平面上通过使用 $ L_{cp} $ 个具有不同斜率的线性调频信号并执行交点处理来解析每个目标的直线，该直线对应于距离-速度平面中的一个点。虽然在逐啁啾基础上进行coherent离散傅里叶变换处理，但一个完整的测量周期因此由（非相干处理的） $ L_{cp} $ 个线性调频信号组成：

$$
T_{\text{CPI}} = T_{cp}, \quad (16)
$$
$$
T_{\text{cyc}} = L_{cp} T_{cp}. \quad (17)
$$

通常使用少量的上啁啾和下啁啾对，如图4所示。为了获得不同的啁啾斜率，通常选择不同的啁啾持续时间，即 $ T_1 \neq T_2 $。然而，在我们的工作中，我们假设 $ T_1 \approx T_2 $，并为简化起见使用单个参数 $ T_{cp} $（或 $ T_{\text{CPI}} $）。对于差异较大的啁啾持续时间，通过使 $ T_{cp} = (T_1 + T_2)/2 $，我们的分析可在平均意义上理解。

由(16)式容易看出，调频连续波雷达的距离和速度分辨率的表达式分别与(13)式和(14)式相同。因此，假设压缩感知和调频连续波雷达在相同频段工作时具有相等的距离和速度分辨率，则可推导出它们的相干处理间隔之间的如下关系：

$$
T^{\text{FMCW}} {\text{CPI}} = T^{\text{CS}} {\text{CPI}}. \quad (18)
$$

另一方面，它们的测量周期持续时间不同

$$
T^{\text{FMCW}} {\text{cyc}} = L^{\text{FMCW}} {cp} T^{\text{CS}}_{\text{cyc}}. \quad (19)
$$

III. 来自连续波和调频连续波雷达的干扰

干扰通常会导致受害雷达频谱中的噪声基底升高 [1],[2],[4]–[6]。在这种准噪声情况下，其影响可以通过信号相对于干扰的抑制增益 $ G_{S/I} $ [1],[6] 来量化，该指标指的是从天线端口到DFT处理后的频率谱之间，目标信号相对于干扰的相对功率增益，而目标检测将在该频谱上进行。换句话说，$ G_{S/I} $ 衡量了受害雷达中干扰相对于目标的抑制效果。基本公式为

$$
G_{S/I} = \frac{T_{\text{CPI}}}{T_{dw}} \cdot G_{sp}, \quad (20)
$$

其中，$ T_{\text{CPI}} / T_{dw} $ 和 $ G_{sp} $ 项分别由AAF和DFT引起。特别地，$ T_{dw} $ 为干扰的驻留时间（dwell time），表示干扰信号处于AAF通带内的持续时间，如图5所示。带宽

AAF的 $ BW_{AAF} $ 由 $ \tau_{\text{max}} = 2R_{\text{max}} / c $ 决定，使得

$$
BW_{AAF} = \alpha \tau_{\text{max}}.
$$

另一方面，信号处理增益 $ G_{sp} $ [19] 来自于DFT的积分，对于目标信号是相干的，而对于类噪声干扰则是非相干的。它等于在相干处理间隔（CPI）内积分的采样点数：

$$
G_{sp} = \frac{T_{\text{CPI}}}{T_s}. \quad (21)
$$

A. 连续波干扰源

假设对连续波干扰采用非相干积分，根据(20)、图5 和(21)可推导出信号与干扰抑制增益：

$$
G_{S/I} = \frac{BW_{sw}}{2BW_{AAF}} \cdot \frac{T_{\text{CPI}}}{T_s} = BW_{sw} T_{\text{CPI}}, \quad (22)
$$

其中假设了Nyquist rate sampling。根据(18)，压缩感知雷达与FMCW雷达在连续波干扰上的抑制增益看似相同。然而，上述表达式虽然对FMCW雷达[6]成立，但在压缩感知雷达中，慢时间上的DFT积分实际上是相干的，因为差频信号在每个慢时间采样点的相位增量（即在整个线性调频脉冲持续时间内积分得到的差频信号瞬时频率）是恒定的。这会在频谱上形成一个谱线峰值，如图6所示，而不是平坦的准噪声底。

由于干扰信号获得了相干信号处理增益

对于 $ N_{cp} $，该谱线峰值的抑制增益可表示为 3

$$
G_{S/I} = BW_{sw} T_{cp}, \quad (23)
$$

比(22)小 $ N_{cp} $ 倍。图6中功率水平为 −35 dB的谱线峰值与根据(23)计算得到的35.9 dB抑制增益相符。当抑制增益不足以将干扰抑制到噪声基底以下时，该谱线峰值将导致虚警目标检测。

B. FMCW干扰源

与连续波干扰不同，FMCW干扰在慢时间维上表现出非相干DFT积分，如图7所示。压缩感知雷达以及调频连续波雷达的信号对干扰抑制增益可以推导为

$$
G_{S/I} = BW_{sw} T_{\text{CPI}} S_F, \quad (24)
$$

其中，与(22)相比额外的比例因子 $ S_F $ [5]，是由于FMCW干扰相对于连续波干扰的驻留时间变化所引起的，并表示为

$$
S_F = \left| \frac{\alpha_I - \alpha}{\alpha} \right|, \quad (25)
$$

其中 $ \alpha_I $ 表示FMCW干扰啁啾斜率。图7中在整个频谱上取平均的仿真干扰基底电平约为 −53.5 dB，与根据(24)式计算得到的54.6 dB的抑制增益一致。4

一个有趣的观察是，CS雷达与FMCW雷达在相互作为受害者时的缓解增益是相同的，前提是它们在第二节-C所述意义上是等效的。具体而言，作为受害者的CS雷达的缓解增益可通过(24)、(18)和(10)推导得出

$$
G^{\text{CS}} {S/I} = BW {sw} N^{\text{CS}} {cp} T^{\text{CS}} {cp} \left| \frac{\alpha^{\text{FMCW}} - \alpha^{\text{CS}}}{\alpha^{\text{CS}}} \right| = BW_{sw} T^{\text{CS}} {cp} (N^{\text{CS}} {cp} \mp 1), \quad (26)
$$

3 公式(23)的表达式也适用于调频连续波雷达。

干扰底噪与典型的噪声基底不同，因为观察到了一些瓣状特性。这会导致后续恒虚警率（CFAR）目标检测的有效噪声电平更高 [19]。

当受害者与干扰源的扫频方向相反时，表达式中的符号变为加号。类似地，FMCW雷达的缓解增益为

$$
G^{\text{FMCW}} {S/I} = BW {sw} T^{\text{FMCW}} {cp} \left| \frac{\alpha^{\text{CS}} - \alpha^{\text{FMCW}}}{\alpha^{\text{FMCW}}} \right| \cdot \frac{1}{N^{\text{CS}} {cp}}
= BW_{sw} T^{\text{FMCW}} {cp} N^{\text{CS}} {cp} (N^{\text{CS}} {cp} \mp 1)
= G^{\text{CS}} {S/I}, \quad (27)
$$

其中附加因子 $ 1/N^{\text{CS}} {cp} $ 反映了 $ N^{\text{CS}} {cp} $ 个干扰的CS线性调频信号进入受害FMCW线性调频信号[21]时的非相干积分。

IV. 来自CS雷达的干扰

A. 虚假目标概率

为了分析由干扰引起的虚幻目标出现情况，我们假设受害者雷达和干扰雷达均为相同的系统，但具有如[2],[5]中所示的均匀随机时间偏移。我们进一步假设测量周期是连续的，中间没有停止间隔。参考图8a，压缩感知雷达中虚幻目标的概率可以被识别为

$$
P^{\text{CS}} {\text{ghost}} = N^{\text{CS}} {cp} \frac{\tau_{\text{max}}}{T^{\text{CS}} {\text{cyc}}}
= \frac{\tau {\text{max}}}{T^{\text{CS}}_{cp}}. \quad (28)
$$

相比之下，调频连续波雷达的虚警概率已在[2],[5]中描述为

$$
P^{\text{FMCW}} {\text{ghost}} = \frac{\tau {\text{max}}}{T^{\text{FMCW}} {\text{cyc}}}
= \frac{\tau {\text{max}}}{L^{\text{FMCW}} {cp} T^{\text{FMCW}} {cp}}, \quad (29)
$$

其中主要区别在于，测量周期中的每个线性调频脉冲都具有不同的斜率，如图8b所示。因此，对于等效的压缩感知和 FMCW雷达，我们得到

$$
P^{\text{CS}} {\text{ghost}} = P^{\text{FMCW}} {\text{ghost}} \times \frac{N^{\text{CS}}_{cp}}{L^{\text{FMCW}}}, \quad (30)
$$

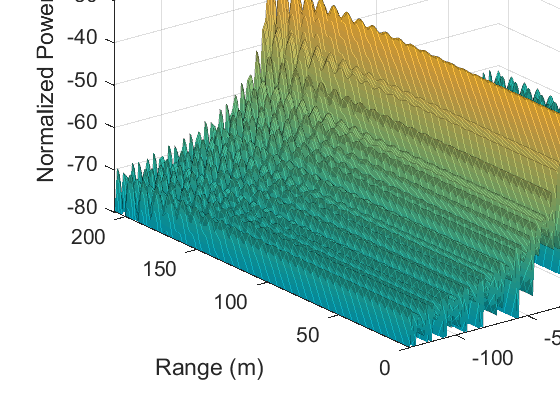
这表明在受害者雷达与干扰雷达完全相同这一理想情况下，CS雷达比FMCW雷达更容易面临虚幻目标出现的风险。然而需要注意的是，线性调频脉冲持续时间的变化很容易破坏CS雷达在慢时间上的DFT积分相干性，导致尖锐的虚幻峰值在随后的图9d中明显平滑化。相反，线性调频脉冲持续时间的变化对FMCW雷达的虚幻目标出现影响很小。

CS雷达情况。)
FMCW雷达情况。)

B. 部分相干情况

如上所述，在具有相同啁啾斜率但不同啁啾持续时间（或扫频带宽）的干扰情况下，FMCW雷达的虚幻目标在产生机制和表现形式上均无显著差异。另一方面，慢时间内的积分会对压缩感知雷达产生不同的影响，如图9所示，其中

$$
\gamma_{cp} = \frac{T^I_{cp}}{T_{cp}}, \quad (31)
$$

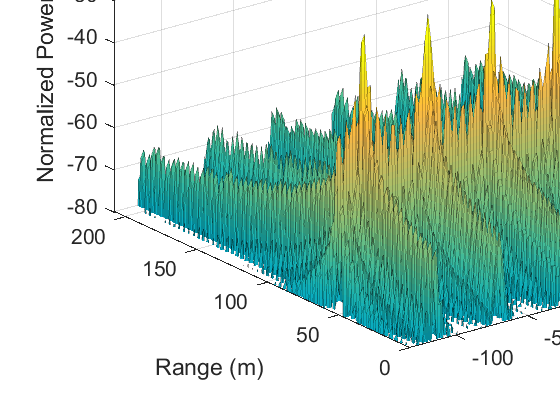
其中 $ T^I_{cp} $ 表示干扰线性调频脉冲的持续时间。在图9a中，以最小整数比表示的 $ \gamma_{cp} $ 为 6/5，这导致一个周期为6个受害者的线性调频信号模式。在此单个周期内，仅有一个干扰线性调频信号恰好位于受害者的AAF通带内。该线性调频信号的快时间频率对应于图中出现的6个虚幻峰值的距离值。所得频谱可理解为将相应快时间频率处的慢时间信号通过一个下采样器，然后通过一个上采样器[18]进行处理，两者的因子均为6。对于图9b的情况，由于 $ \gamma_{cp} $ 的最小整数比为113/100，因此线性调频信号模式每隔113个受害者重复一次，超过了相干处理间隔（CPI）内的总线性调频信号数量，即 $ N_{cp} = 75 $。因此，每个位于AAF通带内的干扰线性调频信号在其快时间频率处产生一个慢时间样本，从而在相应距离上形成平坦的慢时间频谱。当 $ \gamma_{cp} $ 接近1时，图9b中的谱线峰值变得更加接近并开始相互作用，如图9c和9d所示，最终形成目标峰值。

另一方面，虽然具有非相同啁啾斜率的干扰源使得快时间积分变为非相干，但相同的啁啾持续时间仍可保持调频连续波雷达中慢时间的相干积分。第三节-A中描述的连续波干扰情况是一种特殊情况，即干扰信号的啁啾斜率为零。当干扰的啁啾斜率非零且与受害者雷达的斜率差异足够大时，其频谱类似于图6所示的连续波干扰情况，可通过进一步考虑(25)中的比例因子进行简单描述。随着啁啾斜率差值的减小，快时间频率上的谱线峰值不仅会随着比例因子的变化而升高，而且当斜率差小于某一特定值时，谱线峰值开始逐渐集中，最终形成目标峰值[21],[22]。

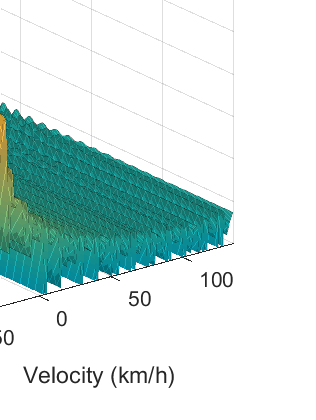(a) $\gamma_{cp}= 1.2$)
(b) $\gamma_{cp}= 1.13$)
(光速) $\gamma_{cp} = 1.001$)
(d) $\gamma_{cp} = 1.0001$)

对应于该特定斜率差的条件称为临界驻留。其特征在于干扰线性调频脉冲在时间和频率上均完全驻留，如图10所示。通过定义

$$
\delta = \frac{\alpha_I}{\alpha} - 1, \quad (32)
$$

斜率差用 $ \delta $ 表示满足

$$
BW_{sw}(1 + \delta) \pm 2\alpha \tau_{\text{max}} = BW_{sw}, \quad (33)
$$

由此可得

$$
|\delta| = \frac{2\tau_{\text{max}}}{T_{cp}}. \quad (34)
$$

假设最大探测距离为 208 米，对于具有表I中参数的压缩感知雷达，我们有 $ |\delta| \approx 0.1 $，这比等效的调频连续波雷达的 $ |\delta| = 0.0014 $ 大 $ N_{cp} = 75 $ 倍。因此，在不考虑慢时相干性的情况下，调频连续波雷达只需略微改变啁啾斜率即可避免虚幻目标，而压缩感知雷达则需要较大的啁啾斜率差。然而，当啁啾持续时间也存在变化时，这种对斜率差的严格要求将大大放宽，如第IV-C节所示。

最后，即使线性调频脉冲的斜率和啁啾持续时间都不同，慢时间上的部分相干性仍可能在频谱中产生谱线峰值，如图11a所示，这种情况可以通过快时间上的非相干积分（如图6所示），随后进行降采样和扩展（如图9a所示）来描述。

C. 准噪声效应

分析由于快时间和慢时间中的非相干性导致的准噪声效应是一项非常复杂的任务。为了使问题更易于处理，我们做出以下假设：

1) 受害者和干扰源的线性调频脉冲斜率相似。特别是，我们假设 $ -1 \leq \delta \leq 1 $。
2) 干扰波形的时间和频率偏移均为中心对齐，使得在时间和频率上均发生最大驻留。

为进一步简化，我们首先考虑受害者雷达的扫频带宽完全相同的情况以及干扰源，如图12所示。注意，差频信号可以近似表示为多个斜率为 $ \alpha_I - \alpha = \alpha\delta $、垂直间距为 $ BW_{sw} $ 的虚拟啁啾。此外，它们的水平间距可表示为 $ BW_{sw}/|\alpha_I - \alpha| = T_{cp}/|\delta| $，从而导致

$$
m_{dw} \approx \left\lceil \frac{T_{\text{CPI}}}{T_{cp}/|\delta|} \right\rceil = \lceil N_{cp} |\delta| \rceil \leq N_{cp} \quad (35)
$$

驻留虚拟啁啾。单个虚拟啁啾对总驻留时间的贡献是 $ 2BW_{AAF}/|\alpha\delta| $，因此

$$
T_{dw} = \frac{2BW_{AAF}}{|\alpha\delta|} \times m_{dw}. \quad (36)
$$

在快时间和慢时间上进行非相干积分后，通过将(36)、(21)和 $ |\delta| = S_F $ 代入(20)，可推导出信号对干扰抑制增益。

$$
G_{S/I} = \frac{N_{cp} T_{cp} |\alpha| |\delta|}{2BW_{AAF} m_{dw}} \cdot \frac{T_{\text{CPI}}}{T_s} = BW_{sw} T_{\text{CPI}} S_F \cdot \frac{N_{cp}}{m_{dw}}, \quad (37)
$$

比由(24)表示的FMCW对FMCW干扰情况下的抑制增益大 $ N_{cp} / m_{dw} \geq 1 $ 倍。图11b中模拟的干扰基底电平约为 −53.8 dB，与根据(37)和(35)计算得到的55.0 dB的计算抑制增益相符。

斜率差导致临界驻留条件满足

$$
|\alpha\delta| \cdot T_{\text{CPI}} = 2BW_{AAF}, \quad (38)
$$

因此

$$
|\delta| = \frac{2\tau_{\text{max}}}{T_{\text{CPI}}}, \quad (39)
$$

这与由(34)给出的FMCW对FMCW干扰情况同样小。此外，由于 $ m_{dw} = 1 $，在抑制增益方面具有 $ N_{cp} $ 倍的优势。

如果扫频带宽不相同，原本应构成单个虚拟线性调频脉冲的短线性调频脉冲段将不再对齐，而必须单独地考虑。然而，(37) 仍然有效，因为在考虑特定的快时间频率bin时不存在根本性差异。关键区别在于 $ m_{dw} $ 现在随bin的不同而变化，因此干扰底噪不再均匀，而是可能沿着快时间频率轴波动，如图11c所示。在表征 $ m_{dw} $ 时一个有用的观察是，短啁啾段在单个受害者啁啾间隔内不重叠，这对负 $ \delta $ 而言是显而易见的。即使对于正 $ \delta $，两个连续啁啾段之间的频率间隔也至少为

$$
BW^I_{sw} - 2 \times |\alpha|\delta \cdot T^I_{cp} = {|\alpha_I| - 2|\alpha|\delta} T^I_{cp} = {|\alpha|(1 + \delta) - 2|\alpha|\delta} T^I_{cp} = (1 - \delta)|\alpha| T^I_{cp} \geq 0, \quad (40)
$$

如图13所示。因此，对于每个快时间频率bin，我们再次得到 $ m_{dw} \leq N_{cp} $，与FMCW对FMCW干扰情况相比，实现了更大的抑制增益。

$\delta= 0.13, \gamma_{cp}= 1.2$)
相同带宽，$\delta= 0.13$)
$\delta= -0.05, \gamma_{cp} = 1.13$)

结论

在本研究中，我们对汽车CS雷达的相互干扰进行了理论分析。考虑了多个波形的虚警目标出现概率以及信干比抑制增益，并与等效FMCW雷达模型进行了比较。各种解析表达式均通过仿真结果得到了验证。研究表明，与FMCW雷达相比，CS雷达总体上具有更强的抗干扰能力，但在虚警目标出现等方面存在更多的边界情况。CS雷达与FMCW雷达之间的干扰效应被证明是等效的。