
来源:深度学习初学者
本文约1800字,建议阅读5分钟了解马尔可夫和隐马尔可夫模型相关基础知识,知道什么是隐马尔可夫模型,知道隐马尔可夫模型可以解决的三个问题及其求解方法。本文目录结构
一、基础知识
马尔可夫性
马尔可夫过程和马尔可夫模型
马尔科夫链
二、隐马尔可夫模型
概念介绍
三要素
两个基本假设
观测序列产生过程
三个基本问题及其求解方法
本文学习目标:了解马尔可夫和隐马尔可夫模型相关基础知识,知道什么是隐马尔可夫模型,知道隐马尔可夫模型可以解决的三个问题及其求解方法。重点是掌握隐马尔可夫模型原理,对于解决的问题及方法,因为还没有做过相关实战,目前只是知道怎么求解即可,之后遇到实际应用时再进一步掌握其使用方法。
一、基础知识
1.马尔可夫性
在介绍隐马尔可夫模型之前先介绍一下什么是马尔可夫性。在某个时刻  的随机变量
的随机变量  与前一个时刻的随机变量
与前一个时刻的随机变量  之间有条件分布
之间有条件分布  , 如果
, 如果 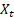 只依赖于
只依赖于  ,而不是依赖于过去的随机变量
,而不是依赖于过去的随机变量 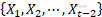 ,这一性质称为马尔可夫性,即:
,这一性质称为马尔可夫性,即:

马尔可夫性,可以通俗的理解为:现在决定未来,而与过去无关

2.马尔可夫过程和马尔可夫模型
马尔可夫过程(Markov process)是一类随机过程,它具有马尔可夫性,因此被称为马尔可夫过程。马尔科夫过程指的是一个状态不断演变的过程,对其进行建模后称之为马尔科夫模型,一个马尔科夫过程就是指过程中的每个状态的转移只依赖于之前的 n个状态,这个过程被称为 n阶马尔科夫模型,其中 n是影响转移状态的数目。最简单的马尔科夫过程就是一阶过程,每一个状态的转移只依赖于其之前的那一个状态。
3.马尔科夫链
具备离散状态的马尔可夫过程,通常被称为马尔可夫链。马尔可夫链是随机变量 S1, … , St 的一个数列(状态集),这些变量的范围,即他们所有可能取值的集合,被称为“状态空间”,而 St 的值则是在时间 t 的状态。如果 St+1 对于过去状态的条件概率分布仅是 St 的一个函数,则:

上述函数可以这样理解:在已知“现在”的条件下,“将来”不依赖于“过去”;或“将来”仅依赖于已知的“现在”。即St+1只于St有关,与St-n, 1<n<t无关。
一个含有 N 个状态的马尔可夫链有 N的平方 个状态转移。每一个转移的概率叫做状态转移概率 (state transition probability),就是从一个状态转移到另一个状态的概率。
二、隐马尔可夫模型
隐马尔可夫模型(Hidden Markov Model,HMM)是用来描述一个含有隐含未知参数的马尔可夫过程。
在马尔可夫模型中,每个状态代表了一个可观察的事件,所以,马尔可夫模型有时又称作可视马尔可夫模型(visibleMarkovmodel,VMM),这在某种程度上限制了模型的适应性。
在正常的马尔可夫模型中,状态对于观察者来说是直接可见的。这样状态的转换概率便是全部的参数。而在隐马尔可夫模型中,状态并不是直接可见的,但受状态影响的某些变量则是可见的。每一个状态在可能输出的符号上都有一概率分布。因此输出符号的序列能够透露出状态序列的一些信息。
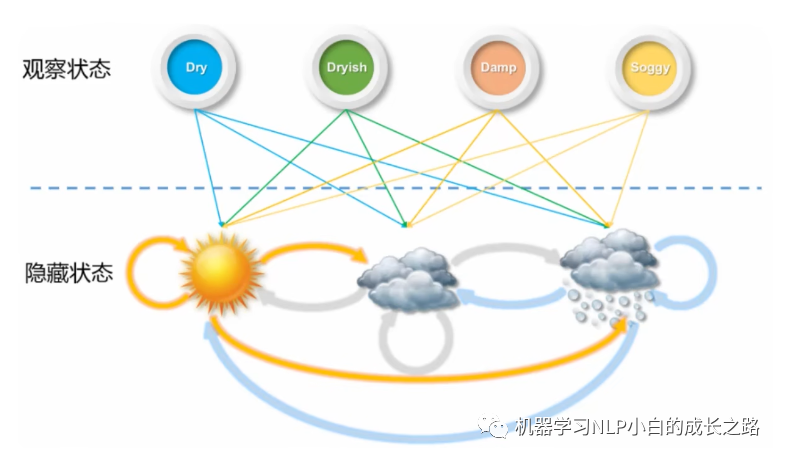
下面通过一个例子理解隐马尔可夫模型,假如我们要预测天气状态的变化序列,但由于某种原因不能直接观察到天气状态,只能通过海藻的状态来推断出天气的状态。海藻的状态有四种,分别是Dry(干燥的)、Dryish(稍干的)、Damp(潮湿的)、Soggy(湿漉漉的)。海藻的状态是可观测的,那它就是 观测状态,天气信息看不到就是 隐藏状态。
1.概念介绍
隐含状态 S。这些状态之间满足马尔可夫性质,是马尔可夫模型中实际所隐含的状态。这些状态通常无法通过直接观测而得到。(例如上面的天气状态)
可观测状态 O。在模型中与隐含状态相关联,可通过直接观测而得到。(例如上面的海藻状态)
初始状态概率矩阵 π。表示隐含状态在初始时刻t=1的概率矩阵
隐含状态转移概率矩阵 A。
观测状态转移概率矩阵 B。有的地方也叫混淆矩阵,表示给定一个隐藏状态后得到的观察状态的概率。
2.三要素
初始状态概率向量π
状态转移概率矩阵A
观测概率矩阵B
一般的,可以用 三元组来简洁的表示一个隐马尔可夫模型。
三元组来简洁的表示一个隐马尔可夫模型。
3.两个基本假设
齐次马尔可夫性假设:即假设隐藏的马尔科夫链在任意时刻t的状态只依赖与其前一时刻的状态,与其他时刻的状态无关,与t时刻也无关
观测独立性假设:即假设任意时刻的观测只依赖于该时刻的马尔科夫链的状态,与其他观测及状态无关
4.观测序列的产生过程
给定隐马尔可夫模型,产生观测序列的过程如下

5.三个基本问题及其求解方法
5.1概率计算问题:
给定模型λ=(Π,A,B)和观测序列O的情况下,求在模型λ=(Π,A,B)下观测序列O出现的概率P(O|λ)。
解决方法:(Forward-Backward 前向算法)
前向概率:给定马尔可夫模型 λ,定义到 t 时刻部分观测序列为o1,o2…ot且状态为qt的概率为前向概率。
前向算法的计算过程如下:

通过一个例子说明前向算法



5.2解码问题:
给定模型λ=(Π,A,B)和观测序列O的情况下,求对给定观测序列P(I | O)最大的状态序列I,即给定观测序列,求最有可能的状态序列。
解决方法:(Viterbi 维特比算法)


接着求t=3时,

5.3学习问题:
观测序列O已知的情况下,求解模型λ=(Π,A,B)参数,使得在该模型下观测序列概率P(O|λ)最大。
解决方法:(极大似然估计算法、最大期望算法)
以上就是隐马尔可夫模型的相关内容,本文参考链接
https://blog.youkuaiyun.com/Island__lee/article/details/124435906
编辑:于腾凯
校对:林亦霖








 本文介绍了马尔可夫性质、马尔可夫链以及隐马尔可夫模型的基础知识,包括隐马尔可夫模型的三要素:初始状态概率、状态转移概率和观测概率。文章详细阐述了隐马尔可夫模型的两个基本假设,并讨论了在给定模型和观测序列下,如何解决概率计算、解码和学习问题,分别提到了前向算法、维特比算法和极大似然估计等求解方法。
本文介绍了马尔可夫性质、马尔可夫链以及隐马尔可夫模型的基础知识,包括隐马尔可夫模型的三要素:初始状态概率、状态转移概率和观测概率。文章详细阐述了隐马尔可夫模型的两个基本假设,并讨论了在给定模型和观测序列下,如何解决概率计算、解码和学习问题,分别提到了前向算法、维特比算法和极大似然估计等求解方法。
















 2万+
2万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








