Day2算法训练（牛牛的快递，最小花费爬楼梯，数组中两个字符串的最小距离）-优快云博客

1.牛牛的快递

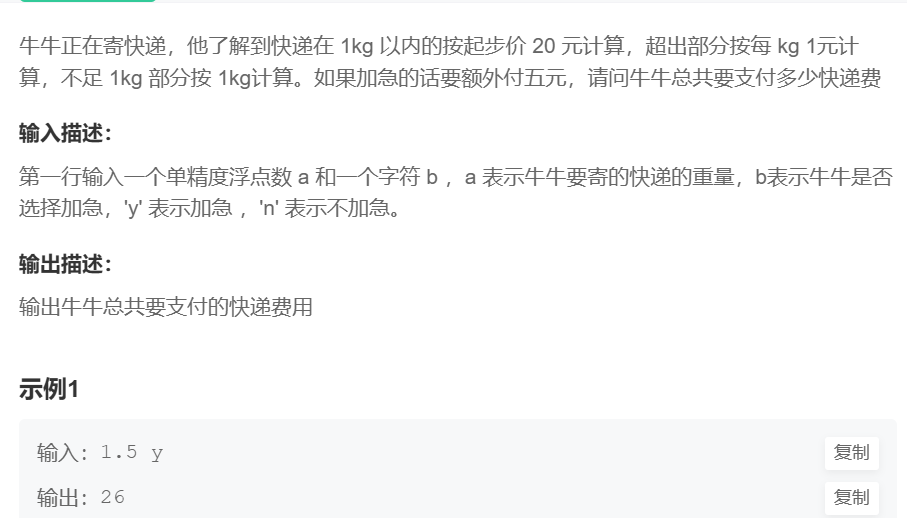
题目内容很简单，跟计程出租车一样；本体唯一需要处理的点就是不足1kg,要按1kg来计算。所以重点解决如何向上取整的问题。

①库函数ceil;#include <cmath>,ceil(c)-->会返回一个向上取整的整数

②强制类型转换。(int)c-->会返回一个向上取整的整数

#include <iostream>
#include <cmath>
using namespace std;

int main() {
    float a;
    char b;
    cin>>a>>b;
    int ret=0;
    if(a<=1)
    {
        ret+=20;
    }
    else {
        ret+=20;
        a-=1;
        a=ceil(a);
        ret+=a;
    }
    if(b=='y')ret+=5;
    cout<<ret<<endl;
    return 0;
}

#include <iostream>
#include <cmath>
using namespace std;

int main() {
    float a;
    char b;
    cin>>a>>b;
    int ret=0;
    if((a-(int)a)>0)
    ret=20+(int)a;
    else
    ret+=20+(int)a-1;
    if(b=='y')ret+=5;  
    cout<<ret<<endl;
    return 0;
}

本题对我的启发主要是读题目时要捋清思路。

2.最小花费爬楼梯

本题没解出来的最重要原因，没有透彻分析清楚题目问题①。这是一个动态规划dp问题

①当我们站在这个台阶上时是不需要花费的，只有继续向上爬才需要花费在这个台阶时的钱

②到底哪里是终点，在最后一个台阶的后一个位置是终点。

对于动态规划问题，我们主要要写出两点

①状态表示：dp[i]表示到达i位置的最小花费,由于题目说可以从下标0开始，也可以从下标1开始，所以dp[0]=dp[1]=0;

②状态转移方程：dp[i]=min(dp[i-1]+cost[i-1],dp[i-2]+dp[i-2])一定要记得加上cost[i-1],cost[i-2]!!!

思路分析：到达一个台阶i,可能是从下标i-1上来的，也可能是从下标i-2上来的，我们取最少花费，如果从i-1上来，则需要支付dp[i-1]即到达i-1位置的最小花费，加上在i-1位置向上爬的花费。【我之前一直没算这个o(╥﹏╥)o】

class Solution {
public:
    int minCostClimbingStairs(vector<int>& cost) {
        int n=cost.size();
        vector<int>dp(n+1);
        dp[0]=0;
        dp[1]=0;
        for(int i=2;i<=n;i++)
        {
            dp[i]=min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2]);
        }
        return dp[n];
    }
};

3.数组中两个字符串的最小距离（模拟+贪心）

可以将本题题意转化，即先简化整数，再去考虑本题的字符串。即给出一个整数数组，给出两个target,（target1,target2）,在数组中找到两个距离最近的target1和target2,并计算出两者间的距离。

在本题中意思就是在一个字符串数组strs中，找到两个距离最近的字符串s1,s2,返回其距离

暴力解法：我们要找到两个字符串之间的最小距离，模拟就是找到所有符合条件的两个字符串，求出其最小距离，利用双层循环，i从前往后扫描，找到target1时再来一个j循环，从0-n来找target2,用ret记录两者之间的距离，但是这样肯定会超时

优化后：贪心dp+预处理（用几个变量来表示前面阶段的最优解）很常用，要记住！！！

进需要遍历一遍数组：

prev1=-1;//用来记录从[0,i]中距离i最近的target1的下标

prev2=-1;//用来记录从[0,i]中距离i最近的target2的下标

ret;//用来记录prev1和prev2之间的最近距离

举个例子：在数组【1,8,2,4,6,8,2,12,3,7】中，找到2和8的最小距离

只需要用i遍历一遍数组，如果i==2,则prev1=i;如果i==8,则prev2=i;每次都记录tmp=abs(prev1-prev2),然后再更新ret=min(ret,tmp)；最后直接返回ret即可。

#include <iostream>
#include <string>
using namespace std;

int main() {
    int n=0;
    cin>>n;
    string str1,str2;
    cin>>str1>>str2;
    string s;
    int prve1=-1,prve2=-1,ret=0x3f3f3f;//要求的ret为最小值，我们初始值就设为最大
    for(int i=0;i<n;i++)
    {
        cin>>s;
        if(s==str1)
        {
            if(prve2!=-1)
            {
                ret=min(ret,i-prve2);
            }
            prve1=i;
        }
        else if(s==str2)
        {
            if(prve1!=-1)
            {
                ret=min(ret,i-prve1);
            }
            prve2=i;
        }
    }
    if(ret==0x3f3f3f)cout<<-1<<endl;
    else cout<<ret<<endl;

    return 0;

}