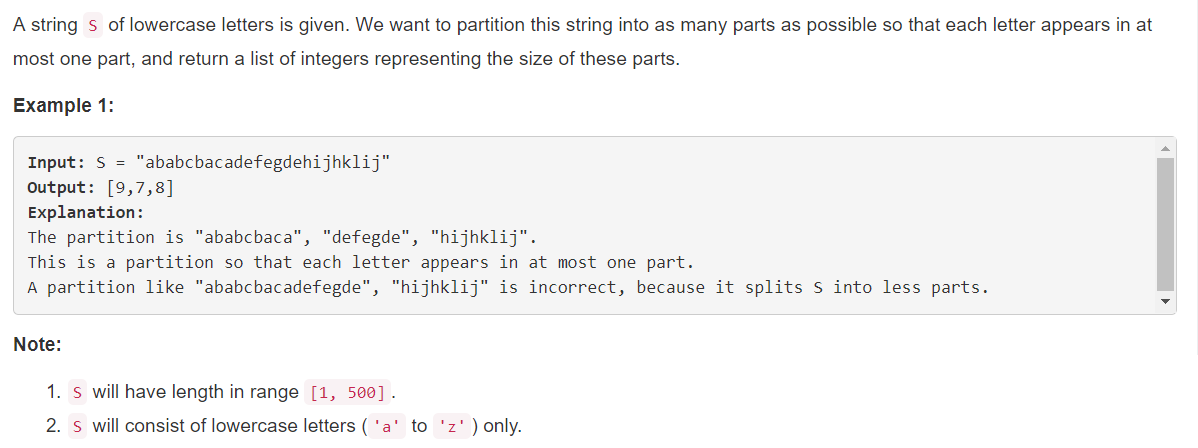
763. Partition Labels

763. Partition Labels

 

我一开始看数据范围很小，没怎么想就直接暴力了。

暴力的思路是：

　　　　对于每一段S的前缀，这个前缀中的每一个字母都不应该在前缀的补集中出现，所以直接循环i：0 to S.length然后对于每一次循环，再循环前缀中的每一个字母，判断是否在后面出现，如果出现就

　　　　说明该前缀不合适继续向后循环，如果没有出现就加入到vector里，并且下一次判断前缀时直接从sum(vector) 开始，所以时间复杂度应该是小于 n² 的。

 1 class Solution {
 2 public:
 3     vector<int> partitionLabels(string S) {
 4         vector<int> ans;
 5         int len = S.size();
 6         int last = 0;
 7         int ex = 0;
 8         for(int i=0;i<len;i++)
 9         {
10              
11             for(int j=ex;j<=i;j++)
12             {
13                 bool p = false;
14                 for(int k=i+1;k<len;k++)
15                 {
16                     if(S[j] == S[k]) {
17                        p = true;
18                        break;
19                     }
20                 }
21                 if(p) {
22                     break;
23                 }
24                 if(j == i) {
25                     ans.push_back(i + 1 - ex);
26                     ex = i+1;
27                 }
28             }
29         }
30         return ans;
31     }
32 };

View Code

线性复杂度的思路：

　　　　后来觉得这样不太好，其实在读题的时候就隐约觉得有O（n）的解法，所以事后想了一下，在一开始先处理每一种字母最后出现的位置。

　　　　然后遍历S时维护一个已遍历前缀中的字母所出现的最大位置，称为lastpos，当遍历到i == lastpos时，说明该前缀中的所有字母都只出现在该前缀。加入vector。

　　　　所以时间复杂度是2n

 1 class Solution {
 2 public:
 3     vector<int> partitionLabels(string S) {
 4         vector<int> ans;
 5         int last[26];
 6         for(int i=0;i<S.size();i++)
 7         {
 8             last[S[i]-'a'] = i;
 9         }
10         
11         int lastpos = 0, ex = 0;
12         for(int i=0;i<S.size();i++)
13         {
14             lastpos = max(lastpos, last[S[i]-'a']);
15             if(lastpos == i) {
16                 ans.push_back(i + 1 - ex);
17                 ex = i + 1;
18             }
19         }
20         return ans;
21     }
22 };

View Code

 

posted @ 2018-01-16 23:23 swallowblank 阅读( ...) 评论( ...) 编辑 收藏