一种圆面积公式的推导方法

原创已于 2022-03-27 16:40:05 修改 · 644 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#android #java #kotlin #抽象代数

于 2022-03-27 16:37:42 首次发布

pdf
文章源码在下面

%请用 XeLaTex 编译
\documentclass{article}
\usepackage{xeCJK}
\XeTeXlinebreaklocale "zh"
% 几何绘图
\usepackage{tikz}
\usetikzlibrary{shapes.geometric,calc,intersections,through}\setcounter{tocdepth}{2}

\begin{document}

\paragraph{}

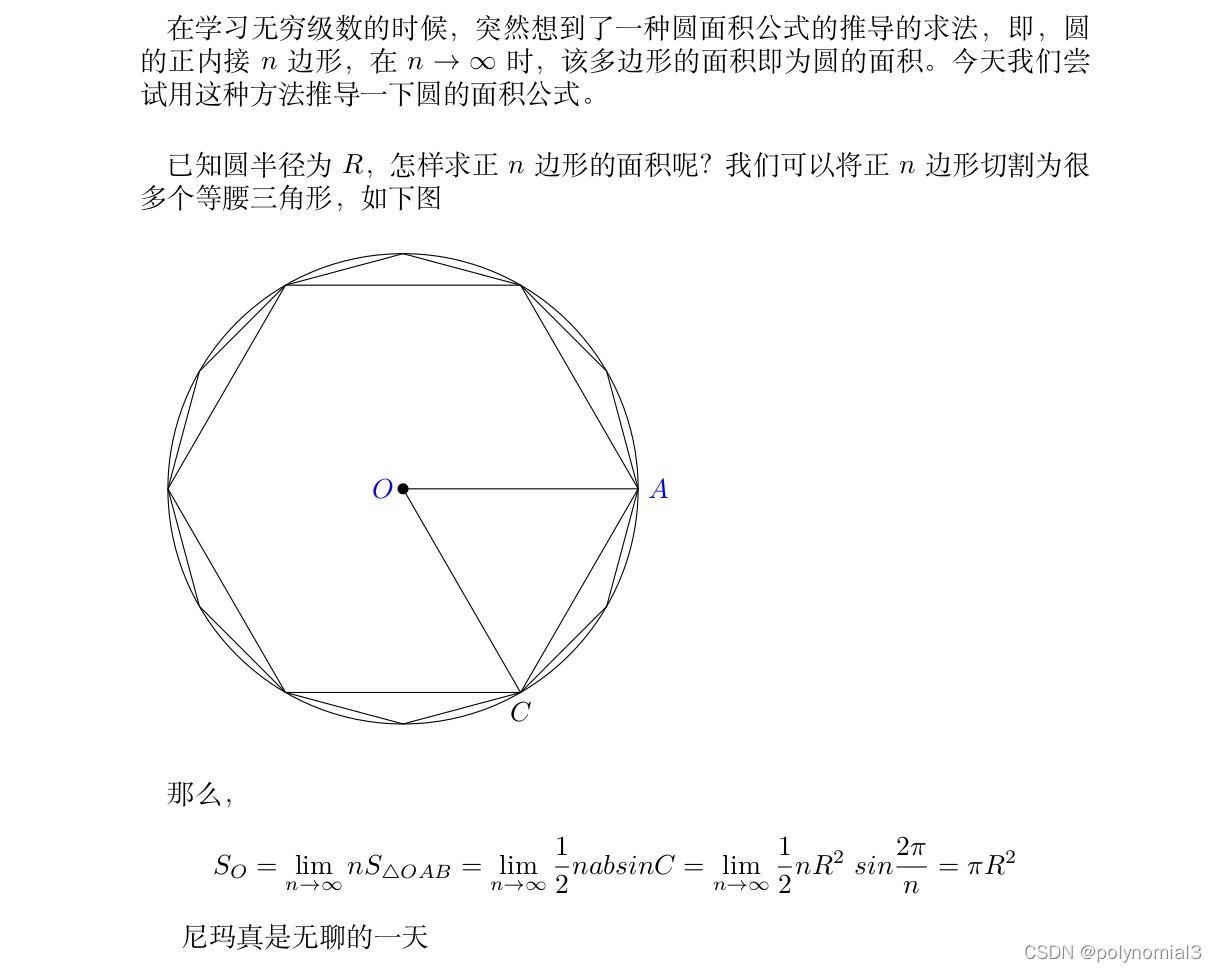
在学习无穷级数的时候，突然想到了一种圆面积公式的推导的求法，即，圆的正内接$n$边形，在$n \to \infty$时，该多边形的面积即为圆的面积。今天我们尝试用这种方法推导一下圆的面积公式。



\paragraph{}

已知圆半径为 $R$，怎样求正 $n$ 边形的面积呢？我们可以将正 $n$ 边形切割为很多个等腰三角形，如下图



\paragraph{}

\begin{tikzpicture}
    \coordinate [label=left:\textcolor{blue}{$O$}] (O) at (0,0);
    \coordinate [label=right:\textcolor{blue}{$A$}] (A) at (3,0);
	
	\draw (O) -- (A);
	
    \node (Z) [name path=Z,draw,circle through=(A)] at (O) {};
	\fill (canvas cs:x=0cm,y=0cm)circle (2pt);
	
	\node[regular polygon,name path=P,
    draw,
    regular polygon sides = 6,
    minimum size = 6cm] (p) at (O) {};
    
    \node[regular polygon,
    draw,
    regular polygon sides = 12,
    minimum size = 6cm,
    shape border rotate=15] (p) at (0,0) {};
    
\path [name intersections={of=Z and P}];
\coordinate [label=below:$C$] (C) at (intersection-6);

\draw (O) -- (C);
    
    
\end{tikzpicture}

\paragraph{}
那么，
$$S_O=\lim_{n \to \infty}nS_{\triangle OAB}=\lim_{n \to \infty}\frac{1}{2}nabsinC=\lim_{n \to \infty}\frac{1}{2}nR^2\ sin \frac{2\pi}{n}=\pi R^2$$

尼玛真是无聊的一天

\end{document}