线性回归 逻辑回归

一. 线性回归

1. 一维变量

线性回归试图学的$f(x_i)=w{x}_i+b$, 使得$f(x_i)\simeq y_i$。
在线性回归中，我们用均方误差来衡量$f(x_i)$与$y_i$之间的差别，使其最小化，即：
$$minF(w,b)=\sum _i^n(f(x_i)-y_i{)}^2$$
通常，我们用最小二乘法对基于均方误差优化的模型进行求解，对$F$求导得：
$$\frac{\partial F}{\partial w}=\sum _i^{n}2x_i(w{x}_i+b-y_i)$$
$$\frac{\partial F}{\partial b}=\sum _i^{n}2(w{x}_i+b-y_i)$$
令导数等于零，得
$$b=\frac{1}{n}\sum _i^n(-w{x}_i+y_i)$$
$$w=\frac{{\sum }_i^n{y}_i(x_i-\frac{1}{n}{\sum }_i^n{x}_i)}{{\sum }_i^n{x}_i^2-\frac{1}{n}({\sum }_i^n{x}_i{)}^2}$$

2. 多维变量

当数据有$d$个属性时，$x$（样本数据）是$n\times d$的矩阵，我们试图学到$f(x)=w{x}^T+b$。令$X=(x^T;1),w=(w;b)$, (1为全1的列向量)，其目标函数为：
$$minF(w^T)=(w^T{X}^T-Y^T{)}^T(w^T{X}^T-Y^T)$$
求导可得：
$$\frac{\partial F}{\partial w}=2(w{X}^T-Y^T)X$$
令导数为零向量，可得：
$$w^T=Y^{T}X(X^{T}X{)}^{-1}$$

3. 从MLE角度理解

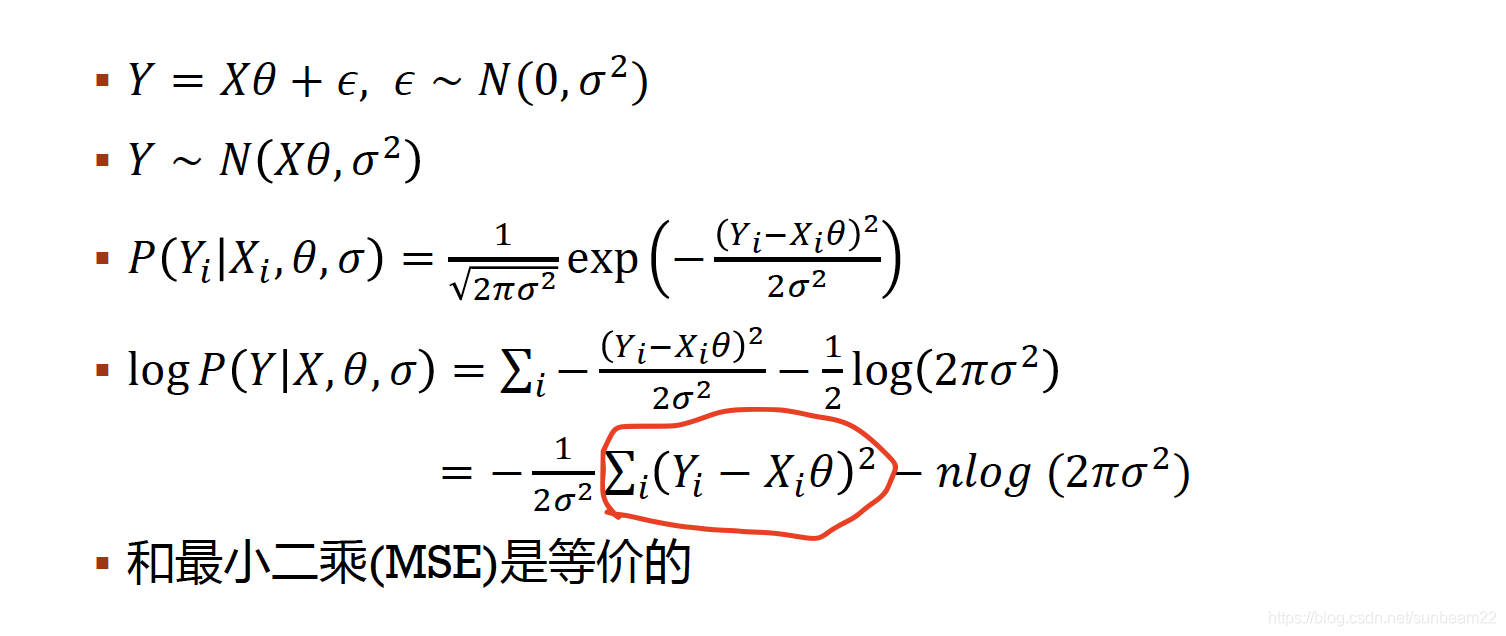
当样本数量很大时，$ϵ$（残差）服从标准正态分布。最大化likelihood，相当于最小化红圈部分，这与线性回归(一维)中的目标函数一致。

二、逻辑回归

逻辑回归其实是一个二分类模型。线性回归模型($f(x_i)=w{x}_i+b$)产生的预测值是实数，我们希望将其转变成$[0,1]$区间上的数，使它代表样本为正的概率$p(y_i=1|x_i)$。对数几率函数是一种"Sigmoid 函数"， 可以帮助实现这一想法：$p(y_i=1|x_i)=\frac{1}{1+e^{-(w^T{x}_i+b)}}$。于是，我们可以通过MLE来估计$w,b$，即最大化对数似然函数：
$$maxln(w,b)=\sum _i^{n}ln(p(y_i|x_i))$$
令$w=(w;b)$,
$$\begin{array}{rl}p(y_i|x_i;w)=& y_i\cdot \frac{e^{w^T{x}_i}}{e^{w^T{x}_i}+1}+(1-y_i)\cdot \frac{1}{e^{w^T{x}_i}+1}\\ =& \frac{1+y_i(e^{w^T{x}_i}-1)}{e^{w^T{x}_i}+1}\end{array}$$
ln(p(yi∣xi;w))=ln(1+yi(ewTxi−1))−ln(ewTxi+1)=yiwTxi−ln(ewTxi+1)    (yi∈{0,1})\begin{aligned} ln(p(y_i|x_i;w))=&ln(1+y_i(e^{w^Tx_i}-1))-ln(e^{w^Tx_i}+1)\\=&y_iw^Tx_i-ln(e^{w^Tx_i}+1)\ \ \ \ (y_i\in\{0,1\}) \end{aligned} ln(p(yi​∣xi​;w))==​ln(1+yi​(ewTxi​−1))−ln(ewTxi​+1)yi​wTxi​−ln(ewTxi​+1)    (yi​∈{0,1})​
目标函数可变为：
$$minln(w)=\sum _i^n-y_i{w}^T{x}_i+ln(e^{w^T{x}_i}+1)$$
一阶导数为：
$$\frac{\partial ln(w)}{\partial w}=\sum _i^n{x}_i\cdot [\frac{e^{w^T{x}_i}}{e^{w^T{x}_i}+1}-y_i]$$
二阶导数为：
$$\frac{{\partial }^{2}ln(w)}{\partial w\partial w^T}=\sum _i^n{x}_i{x}_i^T\cdot \frac{e^{w^T{x}_i}}{e^{w^T{x}_i}+1}\cdot \frac{1}{e^{w^T{x}_i}+1}$$
可以计算得到二阶导数大于零，所以目标函数为凸函数；由于令导数为零无法得到闭式解，我们可用梯度下降法等其他的优化方法来求解。

总而言之，线性回归是拟合一条曲线，使得$l_2$损失最小；逻辑回归是找到一条决策边界，最大化样本分类正确的概率。