此篇文章并非完全原创,参考了下篇博客,如果大家觉得稳重的1、2、3部分不好理解,可以看下图中我的手写版。
http://www.cnblogs.com/pinard/p/6097604.html
支持向量机(Support Vecor Machine,以下简称SVM)虽然诞生只有短短的二十多年,但是自一诞生便由于它良好的分类性能席卷了机器学习领域,并牢牢压制了神经网络领域好多年。如果不考虑集成学习的算法,不考虑特定的训练数据集,在分类算法中的表现SVM说是排第一估计是没有什么异议的。
SVM是一个二元分类算法,线性分类和非线性分类都支持。经过演进,现在也可以支持多元分类,同时经过扩展,也能应用于回归问题。本系列文章就对SVM的原理做一个总结。本篇的重点是SVM用于线性分类时模型和损失函数优化的一个总结。
1. 回顾感知机模型
在感知机原理小结中,我们讲到了感知机的分类原理,感知机的模型就是尝试找到一条直线,能够把二元数据隔离开。放到三维空间或者更高维的空间,感知机的模型就是尝试找到一个超平面,能够把所有的二元类别隔离开。对于这个分离的超平面,我们定义为 w T x+b=0 ,如下图。在超平面 w T x+b=0 上方的我们定义为 y=1 ,在超平面 w T x+b=0 下方的我们定义为 y=−1 。可以看出满足这个条件的超平面并不止一个。那么我们可能会尝试思考,这么多的可以分类的超平面,哪个是最好的呢?或者说哪个是泛化能力最强的呢?

接着我们看感知机模型的损失函数优化,它的思想是让所有误分类的点(定义为M)到超平面的距离和最小,即最小化下式:
当 w和b 成比例的增加,比如,当分子的 w和b 扩大N倍时,分母的L2范数也会扩大N倍。也就是说,分子和分母有固定的倍数关系。那么我们可以固定分子或者分母为1,然后求另一个即分子自己或者分母的倒数的最小化作为损失函数,这样可以简化我们的损失函数。在感知机模型中,我们采用的是保留分子,固定分母 ||w|| 2 =1 ,即最终感知机模型的损失函数为:
如果我们不是固定分母,改为固定分子,作为分类模型有没有改进呢?
这些问题在我们引入SVM后会详细解释。
2. 函数间隔与几何间隔
在正式介绍SVM的模型和损失函数之前,我们还需要先了解下函数间隔和几何间隔的知识。
在分离超平面固定为 w T x+b=0 的时候, |w T x+b| 表示点x到超平面的距离。通过观察 w T x+b 和y是否同号,我们判断分类是否正确,这些知识我们在感知机模型里都有讲到。这里我们引入函数间隔的概念,定义函数间隔 γ ′ 为:
可以看到,它就是感知机模型里面的误分类点到超平面距离的分子。对于训练集中m个样本点对应的m个函数间隔的最小值,就是整个训练集的函数间隔。
函数间隔并不能正常反应点到超平面的距离,在感知机模型里我们也提到,当分子成比例的增长时,分母也是成倍增长。为了统一度量,我们需要对法向量 w 加上约束条件,这样我们就得到了几何间隔 γ ,定义为:
几何间隔才是点到超平面的真正距离,感知机模型里用到的距离就是几何距离。
3. 支持向量
在感知机模型中,我们可以找到多个可以分类的超平面将数据分开,并且优化时希望所有的点都离超平面远。但是实际上离超平面很远的点已经被正确分类,我们让它离超平面更远并没有意义。反而我们最关心是那些离超平面很近的点,这些点很容易被误分类。如果我们可以让离超平面比较近的点尽可能的远离超平面,那么我们的分类效果会好有一些。SVM的思想起源正起于此。
如下图所示,分离超平面为 w T x+b=0 ,如果所有的样本不光可以被超平面分开,还和超平面保持一定的函数距离(下图函数距离为1),那么这样的分类超平面是比感知机的分类超平面优的。可以证明,这样的超平面只有一个。和超平面平行的保持一定的函数距离的这两个超平面对应的向量,我们定义为支持向量,如下图虚线所示。
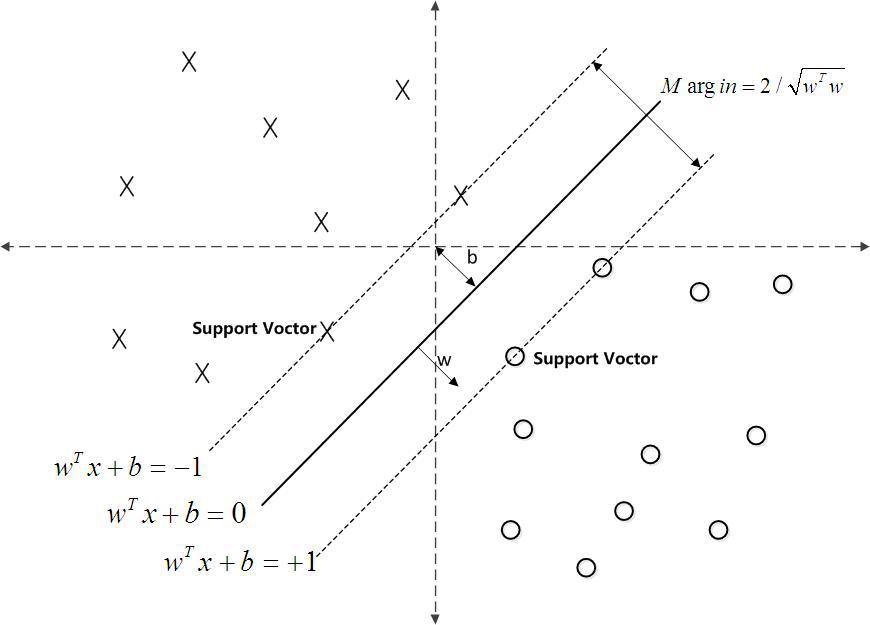
支持向量到超平面的距离为 1/||w|| 2 ,两个支持向量之间的距离为 2/||w|| 2 。
4. SVM模型目标函数与优化
SVM的模型是让所有点到超平面的距离大于一定的距离,也就是所有的分类点要在各自类别的支持向量两边。用数学式子表示为:
一般我们都取函数间隔 γ ′ 为1,这样我们的优化函数定义为:
也就是说,我们要在约束条件 y i (w T x i +b)≥1(i=1,2,...m) 下,最大化 1)||w|| 2 。可以看出,这个感知机的优化方式不同,感知机是固定分母优化分子,而SVM是固定分子优化分母,同时加上了支持向量的限制。
由于 1||w|| 2 的最大化等同于 12 ||w|| 2 2 的最小化。这样SVM的优化函数等价于:





 本文介绍了SVM支持向量机的基本原理,从回顾感知机模型开始,深入探讨了函数间隔与几何间隔的差异,然后引入支持向量的概念。SVM的目标是最大化点到超平面的间隔,通过优化目标函数实现。线性可分SVM的算法过程包括构造约束优化问题、SMO算法求解、计算超平面参数和决策函数。
本文介绍了SVM支持向量机的基本原理,从回顾感知机模型开始,深入探讨了函数间隔与几何间隔的差异,然后引入支持向量的概念。SVM的目标是最大化点到超平面的间隔,通过优化目标函数实现。线性可分SVM的算法过程包括构造约束优化问题、SMO算法求解、计算超平面参数和决策函数。

 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








