1.哈希表，Hash算法

Hash表(又叫散列表)支持我们输入一个key，可以在O(1)的时间复杂度内从Hash表中找到对应的值。

运用的是数组支持按照下标随机访问的时候，时间复杂度是 O(1)
的特性。我们通过散列函数把元素的key值映射为下标，然后将数据存储在数组中对应下标的位置。当我们按照键值查询元素时，我们用同样的散列函数，将键值转化数组下标，从对应的数组下标的位置取数据。

一般一个散列函数满足于以下三点：

• 散列函数计算得到的散列值是一个非负整数，因为底层是数组。
• 如果 key1 = key2，那 hash(key1) == hash(key2)；
• 如果 key1 ≠ key2，那 hash(key1) ≠ hash(key2)。

现实情况是，我们几乎不能找到一个通用的散列函数能够满足于第三点。
当某些情况下可能key1≠key2，但是hash(key1)≠hash(key2)。这就出现了我们常说的Hash冲突。解决hash冲突有两种方案，一种是开放寻址法，一种是链表法。

解决Hash冲突的方案：

先引入散列表的一个概念：装载因子（空位的个数）

散列表的装载因子 = 填入表中的元素个数 / 散列表的长度

1.开放寻址法

其核心思想为如果发现出现了Hash冲突，则重新探测一个位置放下。关于如何探测又分为多种探测方法。其中一个是线性探测，一个是二次探测，一个是Hash探测。一和二的区别主要是探测每次的步长不一样，前者是一次一个步长，后者是1的平方,2的平方。Hash探测是使用第二个散列函数重新计算位置放入。

开放寻址法来解决Hash冲突的时候，有一个不好的地方，是删除的时候不能真的删除，而是标记字段，否则以后查找的时候，发现hash（key）为空（是后被删除的）则判断不存在，导致错误。不管使用哪种探测方法，当数组里面的空值越来越少的时候冲突总会越来越多。所以我们一般要控制空位的比例，也就是上面我们提到的装载因子。开放寻址法不支持负载因子大于1的情况，也比较浪费空间。

但是开放寻址法真的一无是处吗？并不是这样的，开放寻址法底层是数组，可以很好的利用CPU缓存（在一定程度上，万一存储的是大对象，CPU缓存也用不上），而且这种情况下序列化也比较合适，链表法序列化就不太方便，因为链表中的Node节点又包含了Node节点，包含指针，序列化不方便。在某些序列化用的很多的方面，链表法也不太好。

所以一般当数据量小，负载因子也比较小的时候比较适合使用开放寻址法，Java中的ThreadLocalMap就是通过线性探测来解决Hash冲突的。

2.链表法

链表法是Java中HashMap的做法（1.7之前，之后链表修改为了红黑树）

在散列表中，每个“桶（bucket）”或者“槽（slot）”会对应一条链表，所有散列值相同的元素我们都放到相同槽位对应的链表中。

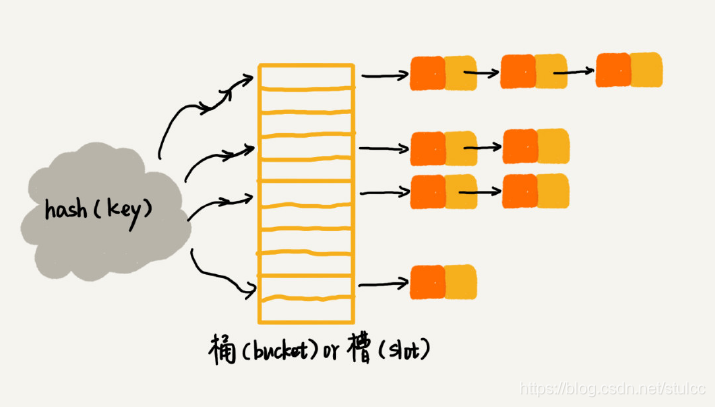当插入的时候，我们只需要通过散列函数计算出对应的散列槽位，将其插入到对应链表中即可，所以插入的时间复杂度是 O(1)。当查找、删除一个元素时，我们同样通过散列函数计算出对应的槽，然后遍历链表查找或者删除。

查找或删除操作的时间复杂度跟链表的长度 k 成正比，也就是 O(k)。对于散列比较均匀的散列函数来说，理论上讲，k=n/m，其中 n 表示散列中数据的个数，m 表示散列表中“槽”的个数。

哈希表非常适合大数据量的比较。比如说Word文档的英文文字错误提示功能，要把所有的英文单词存起来，我们可以计算出所有英文单词的Hash值存储到内存中，当我们输入一个单词后，计算其Hash值，如果存在，再次比对值是否相等，如果不存在，则直接提示错误。内存中的Hash表可大可小（根据电脑内存自己定义）。

如何自己设计一个优秀的哈希表呢？

• 支持快速的查询、插入、删除操作；
• 内存占用合理，不能浪费过多的内存空间；
• 性能稳定，极端情况下，散列表的性能也不会退化到无法接受的情况。

关于散列函数

散列函数不能太简单，否则就会有人非常容易的构造恶意数据插入哈希表，放入一个槽中。那么hash表则就退化为了链表。查询的时间复杂度直接从O(1)变为了O(n)。
散列函数也不能太复杂，否则每次计算一个Key的哈希值，都会大量耗费CPU。
除此之外，Hash函数生成的值要尽可能的均匀分布，这个需要我们根据数据的格式自行实现。

动态扩容解决装载因子过大的问题

对于没有频繁插入和删除的静态数据集合来说，我们很容易根据数据的特点、分布等，设计出完美的、极少冲突的散列函数，因为毕竟之前数据都是已知的。
对于动态散列表来说，数据集合是频繁变动的，我们事先无法预估将要加入的数据个数，所以我们也无法事先申请一个足够大的散列表。随着数据慢慢加入，装载因子就会慢慢变大。当装载因子大到一定程度之后，散列冲突就会变得不可接受。所以我们要进行动态扩容。

针对数组的扩容，数据搬移操作比较简单。但是，针对散列表的扩容，数据搬移操作要复杂很多。因为散列表的大小变了，数据的存储位置也变了，所以我们需要通过散列函数重新计算每个数据的存储位置。
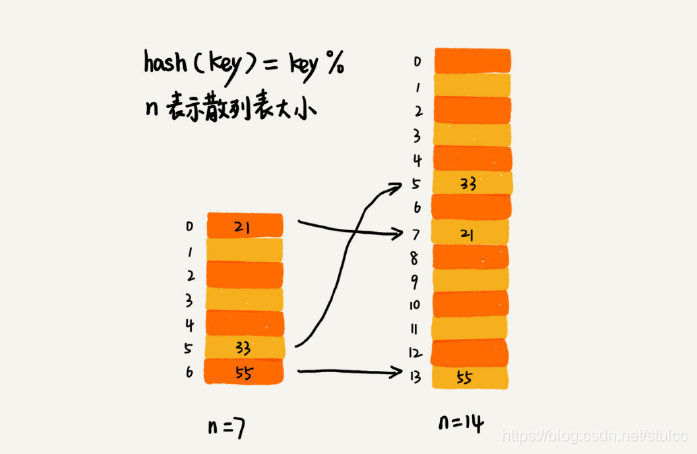插入一个数据，最好情况下，不需要扩容，最好时间复杂度是 O(1)。最坏情况下，散列表装载因子过高，启动扩容，我们需要重新申请内存空间，重新计算哈希位置，并且搬移数据，所以时间复杂度是 O(n)。用摊还分析法，均摊情况下，时间复杂度接近最好情况，就是 O(1)。

在某些情况下，如果哈希表的数据过大，一次性扩容移动数据可能会太慢，我们可能慢慢操作，每次有新数据插入的时候，移动部分数据，分摊一下移动时间。

Hash算法在分布式系统中的应用

负载均衡

对客户端 IP 地址或者会话 ID 计算哈希值，将取得的哈希值与服务器列表的大小进行取模运算，最终得到的值就是应该被路由到的服务器编号。 这样，我们就可以把同一个 IP 过来的所有请求，都路由到同一个后端服务器上。

数据分片

如何快速判断图片是否在图库中

假设现在我们的图库中有 1 亿张图片，很显然，在单台机器上构建散列表是行不通的。因为单台机器的内存有限，而 1 亿张图片构建散列表显然远远超过了单台机器的内存上限。

我们可以对数据进行分片，然后采用多机处理。我们准备 n 台机器，让每台机器只维护某一部分图片对应的散列表。我们每次从图库中读取一个图片，计算唯一标识，然后与机器个数 n求余取模，得到的值就对应要分配的机器编号，然后将这个图片的唯一标识和图片路径发往对应的机器构建散列表。

当我们要判断一个图片是否在图库中的时候，我们通过同样的哈希算法，计算这个图片的唯一标识，然后与机器个数 n 求余取模。假设得到的值是 k，那就去编号 k 的机器构建的散列表中查找。

现在，我们来估算一下，给这 1 亿张图片构建散列表大约需要多少台机器。
散列表中每个数据单元包含两个信息，哈希值和图片文件的路径。假设我们通过 MD5 来计算哈希值，那长度就是 128 比特，也就是 16 字节。文件路径长度的上限是 256 字节，我们可以假设平均长度是 128 字节。如果我们用链表法来解决冲突，那还需要存储指针，指针只占用 8 字节。所以，散列表中每个数据单元就占用 152 字节（这里只是估算，并不准确）。

假设一台机器的内存大小为 2GB，散列表的装载因子为 0.75，那一台机器可以给大约 1000 万（2GB*0.75/152）张图片构建散列表。所以，如果要对 1 亿张图片构建索引，需要大约十几台机器。

在工程中，这种估算还是很重要的，能让我们事先对需要投入的资源、资金有个大概的了解，能更好地评估解决方案的可行性。实际上，针对这种海量数据的处理问题，我们都可以采用多机分布式处理。借助这种分片的思路，可以突破单机内存、CPU 等资源的限制。

一致性Hash算法

假设我们有 k 个机器，数据的哈希值的范围是 [0, MAX]。我们将整个范围划分成 m 个小区间（m 远大于 k），每个机器负责 m/k 个小区间。当有新机器加入的时候，我们就将某几个小区间的数据，从原来的机器中搬移到新的机器中。这样，既不用全部重新哈希、搬移数据，也保持了各个机器上数据数量的均衡。

一致性哈希算法的基本思想就是这么简单。除此之外，它还会借助一个虚拟的环和虚拟结点，更加优美地实现出来。
一致性Hash算法的WiKi链接
一致性Hash算法的百度百科