机器学习到底可不可行？

上一篇讲述了什么是机器学习。是不是感觉发现了新大陆？以后机器学会自己学习后是不是要统治人类的脑洞都冒出来了？但这些仅仅是我们的愿景。我们还得关心一个现实问题：机器到底能不能学习，学得好不好？人是自认为是高等生物，拥有学习能力。其他动物也是有生命的，也会发声，运动，多数通过训练形成条件反射后获得一些额外的能力，但是学习能力低下，多用来供人类玩耍，取乐。

本篇主要讲解机器学习到底行不行？

天下没有免费的午餐——不是所有的事物都可以学习
下图的X有3个特征，D有5个数据集，每一个假设都能对D进行很好的分类。但是整个数据集总共有8种可能，$f_i$可能在空间X的D以外的某一个集合上完全错误。说明假设f只能保证对g有良好的分类能力。这在机器学习上称为没有免费午餐定理（No Free Lunch）。同时也说明了没有任何一个算法能在所有的数据集上都总能产生最准确的学习器。在数据集以外的准确度高，我们称为泛化能力强。通常说某个模型好是基于特定的问题、数据分布、代价函数等等条件下的。例如在均衡问题上的二分类问题，准确率高就可能是一个好的模型，例如预测性别；而在非均衡问题下，精确率就可能是我们更关心的，例如判断是否是高收入者；再例如判断是否要给一个人发信用卡，如果我们的想尽可能的避开风险用户，但是又想抢占市场，这个时候我们可能得用精确率和召回率的调和平均值，也可能为这两者的某个加权平均值，甚至两者的加权调和平均值等等。

Hoeffdings 不等式和PAC（probably approximately correct）
一个罐子里有红球和篮球，通过抽样，将红球的出现频率近似替代罐子里的红球比例。假设u是罐子里的红球占比，v是抽取得到的红球频率。根据Hoeffdings 不等式：

有当N足够大时，u$\approx$v。把结论v=u称为probably approximately correct(PAC)。在统计学上把出现频率当做概率是频率派的学说（后续说到朴素贝叶斯时会说到与他的区别）。

应用Hoeffdings不等式证明机器学习是可行的
定义：$E_{in}(h)为抽样样本上h(x)与y_n不等的概率$
$E_{out}(h)表示在抽样样本以外的数据集上h(x)与y_n不等的概率。$
根据Hoeffdings不等式有
$$P(|E_{in}(h)-E_{out}(h)|>ϵ)\le 2exp(-2{ϵ}^{2}N)$$
$⟹$ 当N足够大时，$E_{in}(h)\approx E_{out}(h)$
$⟹E_{in}(h)足够小时，E_{out}(h)也足够小$
这是否能说明$g\approx f$,机器学习是可行的呢？NONONO！！！
这只能说明在抽样样本和检测样本上两者足够接近，但是却不能确保在这两者之外的数据集上h(x)与y_n不等的概率也小。

BAD SAMPLE概念——常在河边走哪有不湿鞋

150个人丢硬币均抛五次硬币，那么其中至少有一个人连续5次抛硬币结果都为正的概率为，$$1-(31/32{)}^{1}50>99$$
$⟹$ 即使小概率事件，在足够多次实验后，总会发生。
我们学习是不是死记硬背，而是要具有推理能力、能推广到没见过的场景下时，也能解决相应问题。机器学习也一样，只有在整个假设空间下$E_{out}$都很小时，学到的模型才是好的。
如下图，Hoeffdigngs 不等式确保了在大多数的数据集D下，BAD DATA都是小概率事件。但是不同!的数据集在在不同的假设空间上都可能成为bad data。

把Hoeffdigngs 不等式表示为级联形式有：
其中M为数据集假设空间的个数，N为数据集的样本量。可知：
当M有限时，$P_D(DAD|D)$有限。即问题转换为只要M有限，N足够大，$E_{in}$足够小，机器学习是可行的。
那我们直接固定M为1行不行？答案显然是NO！当M很小时，我们可以选择的假设h有限，很难保证$E_{in}$足够小。但是当M很大时，很容易出现bad data或者获取样本的成本急剧增加。那该选取什么样的M呢？

怎样选择M？VC Bound告诉你答案

上面用Hoeffding’s inequality不等式做推导时用了级联，级联假设了各个h之间相互独立，而现实世界中各个hypothesis之间往往或多或少存在交集。即使用级联使概率增大了，也即使不等式右边增大，变相增大了对M的要求。

下面的文章思路：用感知机引入有效线
$⟹$有效hypothesis
$⟹$成长函数和break point
引入Bound function
结合以上三点$⟹$VC Bound

dichotomy

将空间中的点用一条直线分成正类或者负类，$dichotomy\mathcal{H}$是指能将点完全分开的直线种类集合。

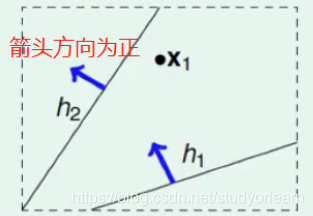
如上图，如果只有一个点的时候，假设箭头方向为正，则在h2附近或者向右，所有的线都把X1点分为负；在h1附近或者向右，所有的线都把X1点分为正。这样所有在h2附近或者向右,平行于h2的线都与h2是一样的效果，把他们归于一类；h1也是同理。这样一来只有一个点时，M为2，$⟹$机器学习可行。
当有2个点时，分类最多3种（在两点之外的2条+两点之间的两条）
当N = 3 时，最多为2^3=8种，如果三点共线，分类为6种（下图中圈住的两种不能用一条直线分开）
当N=4 时，最多有14种。（下图中圈住的不能用一条直线分开，由于对称性，故未7*2 = 14种）
能否假设当N>3时，分类种数<2^N 呢？

增长函数

记$\mathcal{H}对任意N个点的$最大分类种数为$m_{\mathcal{H}}$,称为增长函数。他代表了$\mathcal{H}$的表示能力。反映出了$\mathcal{H}$的的复杂度。
Positive Rays：一条射线，方向指向为正。
当样本点共线时，只使用Positive Rays来做分类，则$$m_{\mathcal{H}}=N+1<<2^{N}s.t.N较大$$
如果样本点形成一个圈，我们可以使用突变多边形来做分类：多边形上的为正，之外为负。则$$m_{\mathcal{H}}=\sum C_N^k=2^N$$

Break Point和shatter

shatter：
对于假设空间$\mathcal{H}$,如果里面的函数能把N个样本的数据集分为所有可能的$2^N类，即m_{\mathcal{H}}=2^N$。则称这N个点被$\mathcal{H}$所shatter。
Break Point：
我们希望M不太大也不太小，如果我们想使用增长函数来代替M，则$m_{\mathcal{H}}$也应不太大也不太小。如果数据被shatter，则$m_{\mathcal{H}}=2^N$,呈指数增加，这肯定不是我们希望的。如果存在一个值k，使$m_{\mathcal{H}}<2^N$，则我们称为我们就称k为$\mathcal{H}$的break point。例如二维感知机的break point为4.
（原英文为If no k inputs can be shattered by H , call k a break point for H .）
从此以后$m_{\mathcal{H}}增速放缓。$
如果$m_{\mathcal{H}}=O(N^{(k-1)}))<poly(N)(多项式)$，则有限且远小于$2^N$，用来替代M，这个时候机器学习是可行的。此时的$m_{\mathcal{H}}<poly(N)(多项式)$

对于break point、成长函数可以参考https://www.zhihu.com/question/38607822/answer/149407083

证明$m_{\mathcal{H}}=O(N^{(k-1)}))<poly(N)(多项式)$

定义：bounding function B(N,k)表示在给定（N,k）下的增长函数上限。则证明转换为
$B(N,k)<poly(N)$

当k= 1 时，B(N,k)恒为1
当k >N 时，$B(N,k)=2^N$
当k = N 时，N是第一个不被shatter的值，$B(N,k)=2^N-1$
如果k<N时，$B(N,k)=O(N^{(k-1)})$成立，则可以使用$m_{\mathcal{H}}$代替M。
下面使用归纳法证明。
B(3,2),此时任意三点中的任意两点不能被shatter，最大值为4.如下图

理解图时先考虑$X_1、X_2，写完前三张后，第四种都为叉叉，出现shatter。$再考虑$（X_1、X_3）、（X_2、X_3）$。对于B(3,2)有B(3,2)=B(2,2)+B(2,1)
B(4,3):此时表示任意4点中的3点不能被shatter。最终结果如下图，共11种，做法和B(3,2)一样。
可以把这11种dichotomy分为orange和purple。orange中在每一个颜色区域，x1、x2、x3是成对出现的，x1是单独的。??????中，x1、x2、x3都不同。则
$$B(4,3)=2\alpha +\beta$$
其中$,\alpha 为orange去掉x4后的去重，\beta 为purple中的个数。$
由于B(4,3) 的任意三个点不能被shatter，则$B(3,3)=\alpha +\beta \le 7$(相当于只取x1、x2、x3，然后去重)。
由于orange中x4是成对出现的，$\alpha 不能被任意三个点shatter⟹\alpha 不能被任意两个点shatter。（如果被2个点shatter了，x4是成对的，则三个点的所有可能都会出现，故肯定能被三个点shatter，矛盾。）$
$⟹\alpha \le B(3,2)$
$⟹\alpha \le B(4,3)\le B(3,3)+B(3,2)$

假想：$B(N,k)\le B(N-1,k)+B(N-1,k-1)$
固定k时，对于B(N+1,k)，任意N+1个点不能被k个点shatter。仍然分为$\alpha 和\beta ,①对\alpha +\beta 中的前N个点去重后一定不能被k个点shatter，则有B(N-1,k)=\alpha +\beta \le B(N,k),道理同上。②对\alpha 部分，\alpha 不能被任意k-1个点shatter,与4个点时同理。$
$⟹B(N,k)\le B(N-1,k)+B(N-1,k-1)$
固定N时，同理可得
$⟹B(N,k+1)\le B(N-1,k+1)+B(N-1,k)$
综上，$⟹对任意的k<N,有B(N,k)\le B(N-1,k)+B(N-1,k-1)$

现再次应用数学归纳法证明：$B(N,k)\le {\sum }_{i=0}^{k-1}{(}_i^N)$
这里应用的是第二数学归纳法，不懂的可以百度下。
当N = 1或k = 1时，结果是显然的。
假设$N\le N_0时，所有的k<N都成立，当N=N_0+1，k<N0时$
$B(N_0+1,k)\le B(N_0,k)+B(N_0,k-1)\le {\sum }_{i=0}^{k-1}{(}_i^{N_0})+{\sum }_{i=0}^{k-2}{(}_i^{N_0})$
$\le {(}_0^{N_0})+{\sum }_{i=1}^{k-1}({(}_i^{N_0})+{(}_{i-1}^{N_0}))+1$
$={(}_0^{N_0+1})+{\sum }_{i=1}^{k-1}{(}_i^{N_0+1})$
$={\sum }_{i=0}^{k-1}{(}_i^N)$
同理可证，当N固定时，k = k+1也成立。
综上$对\forall N,\forall k<N,B(N,k)\le {\sum }_{i=0}^{k-1}{(}_i^N)成立$。
$⟹deg(m_{\mathcal{H}})\le N-1$
即$m_{\mathcal{H}}$是多项式级的。

多项式级的有什么好处？①有限，②增长速度相对$2^N$慢很多，可以得到足够大的M，保证$E_{in}$足够小。

$⟹$如果能找到k<N，可以用$m_{\mathcal{H}}$来替代M。

那我们能否直接这样替换M呢？答案是显然不行的。因为$E_{in}$上的假设可能取值是有限个的，但$E_{out}$上的假设可能取值是无限的。
最终引出Vapnik-Chervonenkis(VC) bound：
$$P[\exists h\in \mathcal{H}s.t.|E_{in}(h)-E_{out}(h)>ϵ]|\le 4m_{\mathcal{H}}(2N)exp(-\frac{1}{8}{ϵ}^{2}N)$$
证明参考https://tangshusen.me/2018/12/09/vc-dimension/中《2.3.3 VC界 》提到的证明连接。

VC Dimension

VC Dimension:在某假设空间$\mathcal{H}$能够被shatter最多的inputs的个数，即最大完全正确的分类能力。根据VC bound可知，VC Dimension的个数d等于break point的个数减1。即$d_{vc}=k-1$,带入VC bound有
$$P[\exists h\in \mathcal{H}s.t.|E_{in}(h)-E_{out}(h)>ϵ]|\le 4(2N{)}^{d_{vc}}exp(-\frac{1}{8}{ϵ}^{2}N)$$
VC Dimension 与演算法、数据分布、目标函数都没有关系。至于模型和假设空间有关

通常$d_{vc}$约等于假设自由变量的数目。其中对于感知机：$d_{vc}=d+1$。d为数据的自由度。

VC Dimension的物理意义

根据Hoeffdings不等式，如果$|E_{out}-E_{in}|>ϵ，出现baddata的几率不超过\delta$,$则P(gooddata)\ge 1-\delta ,可求出E_{out}的置信区间$

右边第二项称为模型复杂度，与样本数量N、假设空间$\mathcal{H}(d_{vc})、ϵ有关。E_{out}由E_{in}$和模型复杂度共同决定。
其中,$d_{vc}、E_{out}、E_{in}之间的关系如下图：随着d_{vc}的增加，模型复杂度一直在增加，E_{out}先增后减，E_{in}一直在减小。所以d_{vc}需要选择合适的大小，否则要么泛化能力差，要么拟合度差。$
样本复杂度：
根据VC bound可以反估需要多少个样本。根据公式需要的样本数约为10000$d_{vc}$，实际中约只需要10$d_{vc}$，说明VC bound很宽松，泛化能力强。造成这一现象的原因主要是：
①使用时霍夫丁不等式是对任意的数据分布、目标函数
②任意的数据集
③$d_{vc}相同的任意\mathcal{H}$
④演算法$\mathcal{A}$可以任意选择g

总结

①天下没有免费的午餐：先举例说明不是所有的事物都可以学习
②引入Hoeffdings不等式和大概可能正确的概念，继而得出结论：当N足够大时，$E_{in}和E_{out}非常接近$
③引入bad sample概念，举例说明即使当前$E_{in}$小，实验次数多了后，总会引发bad sample。继而利用级联引出了可学习的两个条件：

• $E_{in}足够小$
• 样本量N足够大且假设空间$\mathcal{H}$中的势M有限

④级联的缺点：未考虑假设之间的联系，导致等式右边的概率值偏大，对M的要求更高。引出了需求：我们需要不太大也不太小的M。
⑤引入dichotomy、shatter、增长函数、break point的概念，发现在某些情况下，势M会在某个点开始增加缓慢，然后证明了k<N时，$m_{\mathcal{H}}=O(N-1)$。
⑥用$m_{\mathcal H} $代替M，引出VC Bound，继而引出VC Dimension。
⑦通过VC Dimension，得到了机器学习可行的两个条件：

• 能从$\mathcal{H}中选出g，使E_{in}足够小$
• 样本量N足够大且$d_{vc}$有限

⑧解释VC Dimension的物理意义，得到了：为了得到最好的算法，需要选择合适的M，不能太大也不能太小。