seam carving

Seam Carving

andrewdcampbell/seam-carving

17. 如何通过缝隙雕刻图像：Seam Carving

图像智能缩放（Image Retargeting）

智能图像缩放考虑了图像内容的重要性差异，根据“重要的图像内容应该尽可能保留，而相对不重要的内容可以去掉或重复”原则，将原图像缩放为目标尺寸。

智能图像缩放问题转化为：

• 衡量图像内容重要性的方法
  衡量图像内容的重要性的主要方法是计算图中像素的能量值，比较经典的能量计算依据有梯度值（seam carving），图像的显著性（显著性大的地方比较容易受人眼的关注）和网格形变量（Robust Image Retargeting，推荐学习）等。
• 尽可能减弱缩放痕迹的缩放策略

当我们看到一张图像时，人眼最关注的地方就最重要。在上图中，大家的研究最终会停留在那座建筑上，那么那座建筑的重要性就很大。最右列的上下效果分别为seam carving和比例放大的效果图，可以明显看到区别，智能缩放（上图）中建筑没有发生明显形变，图片连贯性和完整性都比较自然；而传统技术（下图）将原图直接拉大，图片内容发生严重变形。而图示中间那一列即为seam carving算法的中间能量示意图，seam carving使用图像的梯度特征进行能量计算。每次针对能量最小的缝（seam）进行移除或复制操作，缩放的过程中需要考虑图像相邻像素的连续性和单调性，以减弱认为处理的痕迹。连续性指的是上下（左右）相邻像素不能在横坐标（纵坐标）方向相差太远，上图中红色的线即为算法检测出的一条缝（seam），该缝是连续的。单调性是为了保证图像始终为矩形形状，每次移除或者复制缝（seam），每行每列只能操作一个像素点，调调性体现在缝的方向是垂直或水平的，不会出现回路形式的缝（seam）。

图像拼接裁剪/缝隙切割（seam carving）

seam carving缝隙切割，就是在图像中找到一条缝，将这条缝插入或删除以达到缩放的目的。是一种用于图像缩放的技术，这种技术可以感知图像的内容，在缩小时保留图像中的重要内容；在放大时，放大图像的重要内容。该方法在保留图像中重要物体方面相对于基于裁剪的缩放方法和等比例缩放技术有明显的优势。
seam carving的基本思想是：图像中不同的位置“能量”不同，有重要内容的地方能量大，反之，可有可无的位置能量小。这个能量函数可以是梯度，梯度大的地方亮度变化剧烈、纹理丰富，一般是重要内容；梯度小的位置亮度变化小，比如蓝天，删除一条缝隙对图像影响较小。

seam carving算法是一种图像缩放算法，它能够将图像缩放也不影响图像的主要内容。

• 计算图像的能量
• 通过能量图计算代价图以及路径图
• 通过代价图以及路径图寻找能量最低的seam
• 重复上述步骤

能量图的计算

“能量”是用来衡量像素的重要程度。如果一个像素有较大的梯度，说明这个像素很大可能Wie边缘。而边缘往往是一幅图像的重要内容。定义能量函数如下去计算每个像素的能量。

遍历图像中每个像素，计算其能量，输出一个与图像相同尺寸的能量图。能量图中边缘像素具有较大亮度，且能量图像也能显现图像的内容。

from skimage import color
import numpy as np
def energy_function(image):
    image_gray = image.copy()
    image_gray = color.rgb2gray(image_gray)
    h,w = image.shape
    G = np.gradient(image)
    out = np.abs(G[0]) + np.abs(G[1])
    return out

计算代价和路径

seam定义为像素从上到下（或从左到右）的连接路径。对于从上到下的像素，从每一行中选取一个像素，这些连接的路径就组成了一条seam。竖直seam（连接方式）为：

n为行数，即相邻两行的连接线只能是当前行像素位置的八连通域子集，即列编号最多相隔一个像素，而非随便连接。同理水平seam定义为：

能量定义了一个像素在图像中的重要程度，为了保留图像汇总的主要内容，删除图像中总能量最低的seam，就保留了图像中的主要内容。对于从上到下的seam。如果一个像素的横坐标为x，那么上一行组成seam的像素的横坐标只能是x-1，x，x+1。那么为了让能量最小，选择上一行这三个像素中能量最小的像素和该像素组成seam，那么通过该点时的总能量为这一点的能量加上上一行像素总能量的最小值，所以利用以下递推公式（从上到下）计算代价：

例如：能量图如下

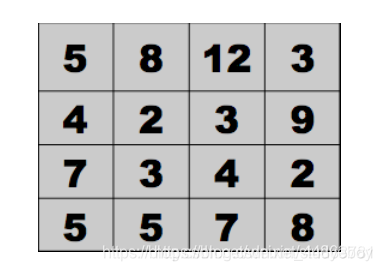
计算代价为：

由于计算到最后一行时，为经过最后一行像素的seam的最小总能量。那么只要挑选总能量最小的像素，并进行回溯，找到这个最小能量对应的seam即可。如果path[i,j]=-1，则找到左上角的像素，如果为path[i,j]=0则回溯至上方像素；path[i,j]=1，回溯至右上方像素。回溯至上一行计算以上操作，直至到达图像第一行。

#计算代价的函数
def compute_cost(image, energy_map, axis=1):
    if axis == 1:
        energy_map = np.transpose(energy_map)
    h, w = energy_map.shape
    energy_cost = np.zeros((h, w))
    path = np.zeros((h, w))
    energy_cost[0, :] = energy_map[0, :].copy()
    for i in range(1, h):
        for j in range(1, w):
            cost_list = np.array([energy_cost[i - 1, j - 1], energy_cost[i - 1, j], energy_cost[i - 1, min(j + 1, w - 1)]])
            index = np.argmin(cost_list)
            energy_cost[i, j] = energy_map[i, j] + cost_list[index]
            path[i, j] = index - 1
        cost_list_left = np.array([energy_cost[i - 1, 0], energy_cost[i - 1, 1]])
        index = np.argmin(cost_list_left)
        energy_cost[i, 0] = cost_list_left[index] + energy_map[i, 0]
        path[i, 0] = index
    if axis == 0:
        path = np.transpose(path)
        energy_cost = np.transpose(energy_cost)
    return path, energy_cost
#回溯函数
def backtrack_seam(path, end_index):
    h, w = path.shape
    seam = -np.ones(h)
    seam[-1] = end_index.copy()
    for i in range(h - 1):
        if path[h - 1 - i, end_index] == -1:
            end_index = end_index - 1
            seam[h - 2 - i] = end_index
        if path[h - 1 - i, end_index] == 0:
            end_index = end_index
            seam[h - 2 - i] = end_index
        else:
            end_index = end_index + 1
            seam[h - 2 - i] = end_index
    return seam
#把seam最小的seam移除图像
def remove_seam(image, seam):
    seam = seam.astype(int)
    if len(image.shape) == 2:
        image = np.expand_dims(image, axis=2)
    h, w, c = image.shape
    image_new = np.zeros((h, w - 1, c))
    for i in range(h):
        image_new[i, :seam[i]] = image[i, :seam[i]] 
        image_new[i, seam[i]:] = image[i, seam[i] + 1:]
    image_new = np.squeeze(image_new)
    return image_new

迭代的寻找seam，并移除

指定图片的尺寸，对图片进行缩小，主要思路是移除一条seam后，在移除的图像上找到另一个seam，然后再移除，重复上述步骤，知道图像到达指定的维度。

def reduce(image, size, axis=1, efunc=energy_function, cfunc=compute_cost, bfunc=backtrack_seam, rfunc=remove_seam):
    if axis == 0:
        image = np.transpose(image, (1, 0, 2))
    image_new = image.copy()
    w = image.shape[1]
    image_gray = color.rgb2gray(image_new)
    energy_map = efunc(image_gray)
    paths, cost = cfunc(image_gray, energy_map, 1)
    index = np.argmin(cost[-1])
    seam = bfunc(paths, index)
    for i in range(w - size):
        image_new = rfunc(image_new, seam)
        image_gray = color.rgb2gray(image_new)
        energy_map = efunc(image_gray)
        paths, cost = cfunc(image_gray, energy_map, 1)
        index = np.argmin(cost[-1])
        seam = bfunc(paths, index)
    if axis == 0:
        image_new = np.transpose(image_new, (1, 0, 2))
    return image_new

seam carving 对图像进行放大处理

利用seam carving找出几条能量最小的seam，在相应位置重复复制这条seam，对图像进行放大。

#该方法速度快，单效果不好
def duplicate(image, seam):
    if len(image.shape) == 2:
        image = np.expand(image, axis=2)
    h, w, c = image.shape
    image_new = np.zeros((h, w + 1, c))
    for i in range(h):
        image_new[i] = np.insert(image[i], int(seam[i