文章目录
- 英文版(原版)
Deep Learning
- 中文版(翻译版)
deeplearningbook-chinese

第一章 引言
人工智能(artificial intelligenc, AI)
- 抽象和形式化的任务
对人类智力来说非常困难,但对计算机来说相对简单的问题(比如,可以通过一系列形式化的数学规则来描述的问题。)可以迅速解决。 - 主观和直观的任务
对人来说很容易执行,但很难形式化描述的任务(比如,人们所说的话或图像中的脸)是人工智能的真正挑战。 - 解决方法
针对这些比较直观的问题,可以让计算机从经验中学习,并根据层次化的概念体系来理解世界,而每个概念则通过与某些相对简单的概念之间的关系来定义。让计算机从经验获取知识,可以避免由人类来给计算机形式的指定它所需要的所有知识。层次化的概念让计算机构建较简单的概念来学习复杂概念。如果绘制出这些概念如何建立在彼此之上的图,将得到一张“深”(层次很多)的图。称这种方法为AI深度学习(Deep Learning)。
知识库(knowledge base)
将关于世界的知识用形式化的语言进行硬编码(hard-code)。计算机可以使用逻辑推理规则来自动的理解这些形式化语言中的声明。
机器学习(machine learning)
依靠硬编码的知识体系面对的困难表明,AI系统需要具备自己获取知识的能力,即从原始数据中提取模式的能力。引入机器学习使计算机能够解决涉及现实世界知识的问题,并能做出看似主观的决策。
表示学习(representation learning)
简单机器学习算法的性能在很大程度上依赖于给定数据的表示(representation)。然而,对于许多任务来说,很难知道应该提取哪些特征。解决这个问题的途径之一是使用机器学习来发掘表示本身,而不仅仅把表示映射到输出。学习到的表示往往比手动设计的表示表现的更好。并且他们只需最少的人工干预,就能让AI系统迅速适应新的任务。
深度学习(Deep Learning)
表示学习从原始数据中提取高层次、抽象的特征是非常困难的。深度学习通过其他较简单的表示来表达复杂,解决了表示学习中的核心问题。深度学习让计算机通过较简单概念构建复杂的概念。
第一部分 应用数学与机器学习基础
第二章 线性代数
线性代数作为数学的一个分支,广泛应用于科学和工程中,线性代数主要是面向连续数学。
范数

特征分解
通过分解矩阵来发现矩阵表示成数组元素时不明显的函数性质。

奇异值分解


Moore-Penrose伪逆


迹
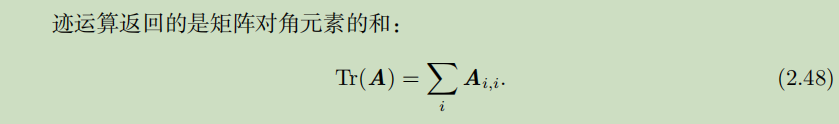
行列式

第三章 概率与信息论
概率论是用于表示不确定性声明的数学框架。它不仅提供了量化不确定性的方法,也提供了用于导出新的不确定性声明(statement)的公理。在人工智能领域,概率论主要有两种用途。首先,概率法则告诉AI系统如何推理,据此设计一些算法来计算或者估算由概率论导出的表达式。其次,可以用概率和统计从理论上分析提出的AI系统的行为。
概率论能够提出不确定的声明以及在不确定性存在的情况下进行推理,而信息论能够量化概率分布中的不确定性总量。
信息论
信息论是应用数学的一个分支,主要研究的是对一个信号包含信息的多少进行量化。
信息论的基本想法是一个不太可能的事件居然发生了,要比一个非常可能的事件发生,能提供更多的信息。
需要通过这种基本想法来量化信息。特别的,
- 非常可能发生的事件信息量要比较少,并且极端情况下,确保能够发生的事件应该没有信息量。
- 较不可能发生的事件具有更高的信息量。
- 独立事件应具有增量的信息。




结构化概率模型


第四章 数值计算
机器学习算法通常需要大量的数值计算。这通常是指通过迭代过程更新解的估计值来解决数学问题的算法,而不是通过解析过程推导出公式来提供正确解的方法。常见的操作包括优化(找到最小化或最大化函数值的参数)和线性方程组的求解。对数字计算机来说实数无法在有限内存下精确表示,因此仅仅是计算涉及实数的函数也是困难的。
基于梯度的优化方法
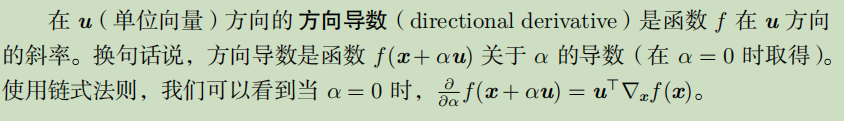

梯度之上: Jacobian和Hessian矩阵
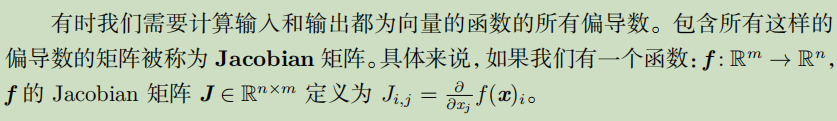




约束优化



第五章 机器学习基础
机器学习本质上属于应用统计学,更多的关注于如何用计算机统计的估计复杂函数,不太关注为这些函数提供置信区间。
学习算法
对于某类任务T和性能度量P,一个计算机程序被认为可以从经验E中学习是指,通过经验E改进后,它在任务T上由性能度量P衡量的性能有所提升。
任务T
通常机器学习任务定义为机器学习系统应该如何处理样本(example)。样本是指从某些希望机器学习系统处理的对象或事件中收集到的已经量化的特征(feature)的集合。
性能度量P

经验E
根据学习过程中的不同经验,机器学习算法可以大致分类为 无监督(unsupervised)算法和 监督(supervised)算法。
估计、偏差和方差
统计领域为我们提供了很多工具来实现机器学习目标,不仅可以解决训练集上的任务,还可以泛化。基本的概念,例如参数估计、偏差和方差,对于正式地刻画泛化、欠拟合和过拟合都非常有帮助。
点估计

偏差




方差和标准差

最大似然估计


最大似然估计(Maximum Likelihood Estimation, MLE)与最大后验估计(Maximum A Posteriori Estimation, MAP)
贝叶斯统计



监督学习算法
支持向量机



第二部分 深度网络:现代实践
第六章 深度前馈网络



基于梯度的学习
代价函数


第三部分 深度学研究
参考资料
为什么样本方差(sample variance)的分母是 n-1?
为什么样本方差(sample variance)的分母是 n-1?
Prove that E(X¯¯¯¯−μ)2=1nσ2
机器学习概率基础-高斯分布相关重要知识推导
浅析最大似然估计与最大后验估计








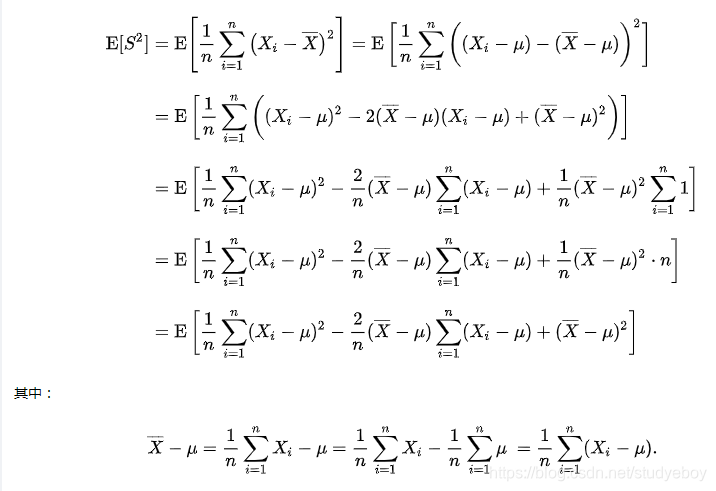





















 574
574

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








