二叉树的顺序存储

二叉树的顺序存储结构是把二叉树的所有节点按照一定的次序顺序存储到一组包含n个存储单元的空间中。在二叉树的顺序存储结构中只存储节点的值，不存储节点之间的
逻辑关系，节点之间的逻辑关系由数组下标的顺序来体现。
二叉树的顺序存储原则是：不管给定的二叉树是不是完全二叉树，都看做完全二叉树。即按完全二叉树的层次次序把各个节点依次存入数组中。

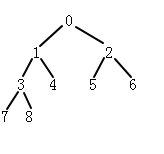
如图所示二叉树存放在数组中就是{0,1,2,3,4,5,6,7,8}
二叉树的顺序存储结构是把二叉树的所有节点按照一定的次序顺序存储到一组包含n个存储单元的空间中。在二叉树的顺序存储结构中只存储节点的值，不存储节点之间的
逻辑关系，节点之间的逻辑关系由数组下标的顺序来体现。
二叉树的顺序存储原则是：不管给定的二叉树是不是完全二叉树，都看做完全二叉树。即按完全二叉树的层次次序把各个节点依次存入数组中。

如图所示二叉树存放在数组中就是{0,1,2,3,4,5,6,7,8}

public class SeqEcTree{
//默认树的深度为5
private static int DEFAULT_DEEP=5;
//树的深度
private int deep;

private Object[] datas;
//总数
private int size = 0;

public SeqEcTree() {
	// TODO Auto-generated constructor stub
	this(DEFAULT_DEEP);	
}

public SeqEcTree(int dept) {
	this.deep = dept;
	int length = (int) Math.pow(2, dept);
	datas = new Object[length];
}

/**
 * 添加
 * @param t 元素
 * @param parent 父索引
 * @param isLeft 是否为左子树
 */
public void add(T t,int parent,boolean isLeft) {
	if(datas[parent]==null) {
		throw new RuntimeException("index["+parent+"] is not Exist!");
	}
	if(t==null) {
		throw new NullPointerException();
	}
	if(isLeft) {
		checkIndex(parent*2+1);
		if(datas[parent*2+1]!=null) {
			throw new RuntimeException("index["+parent*2+1+"] is  Exist!");
		}
		datas[parent*2+1]=t;
	} else {
		checkIndex((parent+1)*2);
		if(datas[(parent+1)*2]!=null) {
			throw new RuntimeException("index["+(parent+1)*2+"] is  Exist!");
		}
		datas[(parent+1)*2]=t;
	}
	size++;
}

//检查角标越界
private void checkIndex(int index) {
	if(index<0||index>=datas.length) {
		throw new IndexOutOfBoundsException();
	}
}

 // 判断二叉树是否为空  
public boolean isEmpty() {  
    return datas[0] == null;  
}  

// 获取根节点  
public T getRoot() {  
    return (T) datas[0];  
}  

// 返回指定节点的父节点  
public T getParent(int index) {
	checkIndex(index);
    if (index == 0) {  
        throw new RuntimeException("根节点不存在父节点！");  
    }  

    return (T) datas[(index - 1) / 2];  
}  
  
//获取右子节点  
public T getRight(int index){  
    checkIndex((index+1)*2);
    return (T) datas[index * 2 + 2];  
}  
  
//获取左子节点  
public T getLeft(int index){  
    checkIndex(index*2+1);  
    return (T) datas[index * 2 + 1];  
}  
  
//返回该二叉树的深度  
public int getDeep(){  
    return deep;  
}  

//总共有多少个结点
public int size() {
	return size;
}
//返回指定数据的位置  
public int indexOf(T data){  
   if(data==null){
	 //不能为空
	 throw new NullPointerException();
   } else {
	   for(int i=0;i<datas.length;i++) {
		   if(data.equals(datas[i])) {
			   return i;
		   }
	   }
   }
    return -1;  
}  

}