本文介绍了几种高效的素数判断方法，并通过C语言实现。同时，还探讨了数组的线性搜索、二分搜索及排序算法，包括选择排序的具体实现。
目录
法三： 只需从3到sqrt（x）即可，其余同上；只需要循环sqrt（x）遍。
数组运算
素数判断——高级
法一：从2到x测试是否能整除
#include<stdio.h>
int isPrime(int x)
{
int ret = 1;
int i;
if ( x == 1 ) ret = 0;
for ( i=2; i<x; i++ ){
if( x % i == 0 ){
ret = 0;
break;
}
}
return ret;
}
int main(void)
{
int x;
scanf("%d",&x);
if( isPrime(x) ){
printf("%d是素数\n",x);
}else {
printf("%d不是素数\n",x);
}
return 0;
}（对于n要循环n-1遍，当n很大时近似于n遍）
法二：去掉偶数后，从3到x-1，每次加2
int isPrime(int x)
{
int ret = 1;
int i;
if ( x == 1||(x%2==0&&x!=2)) ret = 0;
for ( i=3; i<x; i+=2 ){
if( x % i == 0 ){
ret = 0;
break;
}
}
return ret;
}若x是偶数，则立刻可以测出来，否则需要循环（x-3)/2-1遍，当x很大时就是x/2遍。
法三： 只需从3到sqrt（x）即可，其余同上；只需要循环sqrt（x）遍。
以上三种方法都是用比x小的数来测试。接下来让我们采用比x小的素数来进行测试。
法四：判断是否能被已知的比x小的素数整除。
#include<stdio.h>
int isPrime(int x,int knownPrimes[], int numberOfKnownPrimes) //创建一个函数测试是否为素数
{
int ret = 1;
int i;
for ( i=0; i<numberOfKnownPrimes; i++ ){
if( x % knownPrimes[i] == 0 ) {
ret = 0;
break;
}
}
return ret;
}
int main(void)
{
const int number = 100; //表内有100个元素
int prime[number] = {2}; //表中第一个素数是2，放进第一个位置上
int count = 1; //定义count来表示表中已有的数目，后面用来作为位置的序号
int i = 3; //从 3开始来测试是否为素数
while ( count < number ){
if( isPrime(i,prime,count)){
prime[count++] = i; //把满足isPrime的i放进表（数组）中，同时count++用来把空位留给下一个素数
}
i++;
}
for ( i= 0; i<number; i++) {
printf("%d",prime[i]);
if ((i+1)%10) printf("\t"); //使数组格式化输出,即每十个一行
else printf("\n");
}
return 0;
}
现要查看程序运行过程中变量的变化，可以采用debug，也可以在程序中插入一些输出语句
#include<stdio.h>
int isPrime(int x,int knownPrimes[], int numberOfKnownPrimes) //创建一个函数测试是否为素数
{
int ret = 1;
int i;
for ( i=0; i<numberOfKnownPrimes; i++ ){
if( x % knownPrimes[i] == 0 ) {
ret = 0;
break;
}
}
return ret;
}
int main(void)
{
const int number = 9; //表内有100个元素
int prime[number] = {2}; //表中第一个素数是2，放进第一个位置上
int count = 1; //定义count来表示表中已有的数目，后面用来作为位置的序号
int i = 3; //从 3开始来测试是否为素数
{ //插入一个表头,此处的i只在创建表头的这段中存在
int i;
printf("\t\t\t");
for (i=0;i<number;i++){
printf("%d\t",i);
}
printf("\n");
}
while ( count < number ){
if( isPrime(i,prime,count)){
prime[count++] = i; //把满足isPrime的i放进表（数组）中，同时count++用来把空位留给下一个素数
}
{
printf("i=%d\tcount=%d\t\t",i,count);
int i; //i只存在于遍历数组输出时
for(i=0;i<number;i++){
printf("%d\t",prime[i]);
}
printf("\n");
}
i++;
}
for ( i= 0; i<number; i++) {
printf("%d",prime[i]);
if ((i+1)%5) printf("\t"); //使数组格式化输出,即每十个一行
else printf("\n");
}
return 0;
}
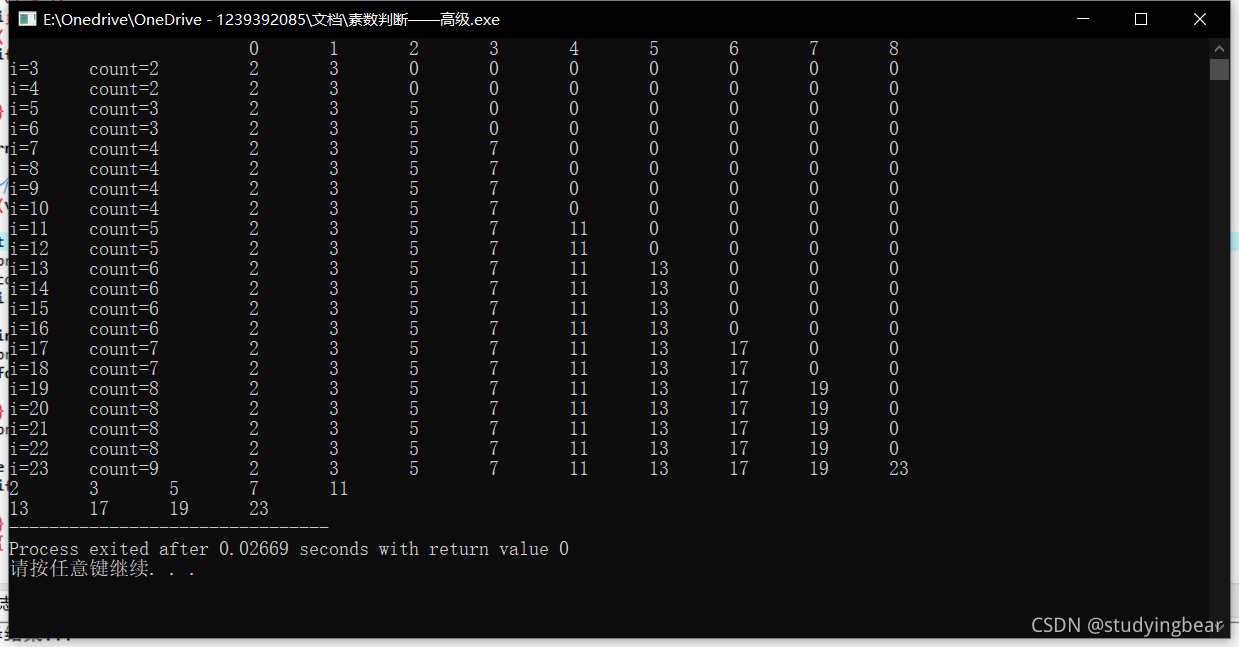
以上四种方法，虽逐步提高了代码运算的速度，使循环的次数越来越少，但都是再构造一些数做整除，只不过构造的用来除它的数越来越少。但其实可以反过来思考，用以下方法来构造素数表：
欲构造n以内的素数表：
1.令x为2
2.将2x、3x、4x直到ax<n的数标记为非素数
3.令x为下一个没有被标记为非素数的数，重复2；直到所有的数，重复2；直到所以的数都已经尝试完毕
#include<stdio.h>
int main()
{
const int maxnumber = 100;
int isPrime[maxnumber];
int i; //开辟数组，初始化其所有元素为1，isPrime[x]为1表示x是素数
for(i=0;i<maxnumber;i++){
isPrime[i]=1;
}
int x=2;
for(x; x<maxnumber; x++){
if( isPrime[x] ){
for(i=2; x*i<maxnumber; i++){
isPrime[x*i] = 0;
}
}
}
for(x=2; x<maxnumber; x++){
if( isPrime[x] ){
printf("%d ", x);
}
}
return 0;
}总结：算法不一定和人的思考方式相同，
搜索
线性搜索
使用search函数
#include<stdio.h>
int search(int key,int a[],int len)
{
int i;
for(i=0; i < len; i++){
if(key==a[i]){
break;
}
}
if( i == len ){
return 1;//循环走完了也没跳出来，说明没找到位置
}else{
return i;
}
}
int main(){
int a[]={1,23,2,4,5,44,55,6,7,777};
int r = search(2,a,sizeof(a)/sizeof(a[0]));
printf("%d\n",r);
return 0;
}虽然可行，但也违背了一个原则：一个变量承担了两个责任，i变量既是循环遍历用的变量，又用来表达到底有没有找到那个数的位置。所以这不是一个好代码。
以下这种方法则是我们喜欢的形式：
#include<stdio.h>
int search(int key,int a[],int len)
{
int i;
int ret = -1; //需要有返回结果的变量
for(i=0; i < len; i++){
if ( key == a[i] ){
ret = i; //但找到这个位置是用i记下来
break; //单一出口
}
}
return ret;
}
int main(){
int a[]={1,23,2,4,5,44,55,6,7,777};
int r = search(44,a,sizeof(a)/sizeof(a[0]));
printf("%d\n",r);
return 0;
}搜索的例子
如果输入一个数字，要搜索出这个数字对应的名字。（如美元中每种硬币对应的名字）
做法：把数字看成一个数组，把名字看成一个数组
#include<stdio.h>
int amount[] = {1,5,10,25,50};
char *name[] = {"penny","nickel","dime","quarter","half-dollar"};
int search(int key,int a[],int len)
{
int i;
int ret = -1;
for(i=0; i < len; i++){
if ( key == a[i] ){
ret = i;
break;
}
}
return ret;
}
int main(){
int k;
scanf("%d",&k);
int r = search(10,amount,sizeof(amount)/sizeof(amount[0]));
if ( r>-1 ){
printf("%s\n",name[r]);
}
return 0;
}但是这个做法使得数组割裂开， 以后深入学习后会发现这是一种不好的代码。涉及到指针，在此不深入。
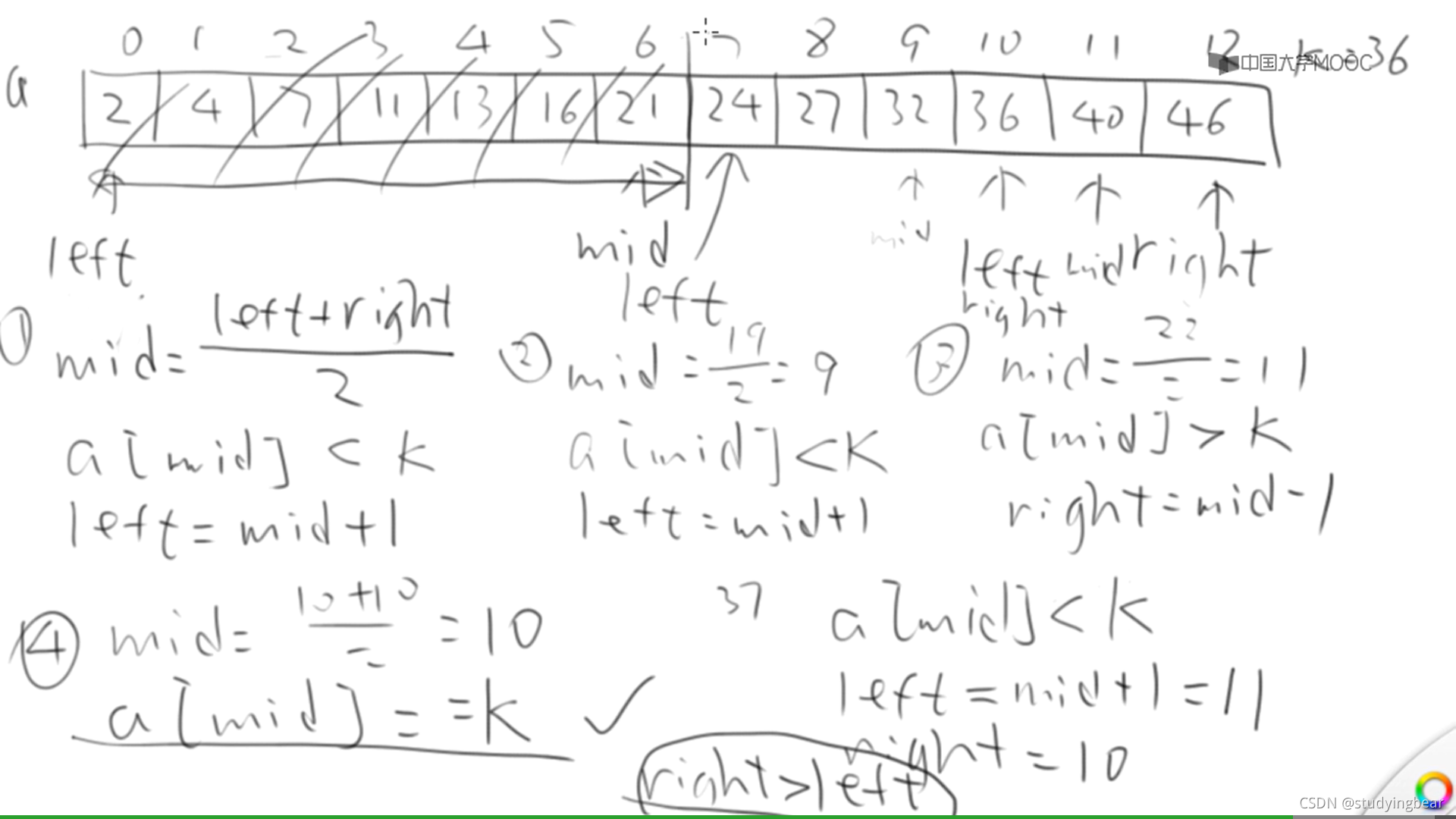
二分搜索
#include<stdio.h>
int amount[]={1,2,3,4,5,6,7,8,9,10};
int search(int key,int a[],int len)
{
int ret = -1;
int left = 0;
int right = len - 1 ;
while(right > left){
int mid = (left + right) / 2;
if(a[mid]==key){
ret = mid;
break;
}else if(a[mid]>key){
right = mid - 1;
}else{
left = mid + 1;
}
printf("%d\n",mid);
}
return ret;
}
int main(){
int k;
scanf("%d",&k);
int r = search(k,amount,sizeof(amount)/sizeof(amount[0]));
if ( r>-1 ){
printf("%d\n",r);
}else{
printf("没在这");
}
return 0;
}二分搜索最大的好处就是效率高。对于有n个数的数组来说，要找到某个元素的位置，最多需要搜索log2 n次。
排序初步
已知使用二分搜索时数组中的数字都是按从大到小排序的，接下来我们来学习如何将无序的数组排成有序的。
法一：
step1：找出最大数所在的位置(定义一个函数），先拿第一个过来，当它是最大的，遍历数组，逐个与maxid上的数比较大小。
step2: 把找到的最大数挪到最后面去（即让最末尾位置上的数与最大数交换位置）。
step3: 遍历，重复做1、2的步骤，直到把所有数从小到大排列。
#include<stdio.h>
int max(int a[],int len) //step1
{
int maxid=0;
int i;
for(i=0; i<len ;i++){
if(a[maxid]<a[i]){
maxid = i;
}
}
return maxid;
}
int main()
{
int a[] = {2,123,23,231,78,34,62,234,1344,13};
int len = sizeof(a)/sizeof(a[0]);
int i;
for(i=len-1; i>0; i--){ //step3
int maxid = max(a,i+1);
//step2:exchange:a[maxid],a[len-1]
int t = a[maxid];
a[maxid] = a[i];
a[i] = t;
}
for(i=0; i<len; i++){
printf("%d\t", a[i]);
}
return 0;
}法二：
step1：输入要排序的个数，遍历输入要进行排序的数字。
step2：n个数，总共需要进行n-1次大循环，每一个大循环结束后，后面的数被依次固定为最大的数。因为n-1个数排完，第一个数一定已经归位了，所以只需进行n-1次。
step3：每一次大循环里面，又要进行遍历，即进行n-i-1次左右两数之间的比较和换位把最大的数放到后面。小循环内部进行n-i-1次的原因就是我每进行一次大的循环，就可以确定后面一位的数字而不用再进行比较，所以每个大循环中小循环进行的次数逐步减少，且为n-i-1。
#include <stdio.h>
int main(void)
{
int a[1001];
int n, i, j, t;
scanf("%d", &n); //step1
for(i = 0; i < n; i++)
{
scanf("%d", &a[i]);
}
//step2
for(i = 0; i < n - 1;i++)
{
//step3
for(j = 0; j < n - i - 1; j++)
{
if(a[j] > a[j + 1])
{
t = a[j]; //exchange
a[j] = a[j + 1];
a[j + 1] = t;
}
}
}
for(j = 0; j < n; ++j) //遍历输出排序结果
{
printf("%-5d ", a[j]);
}
return 0;
}
法二是从第一位开始和它后面的这个数进行比较，如果我比你大，我和你交换位置，相当于往后移一位，这样最大的数字就被放到最后面了。
法一是先找出一段数字内的最大数（其实和法二是一样的比较方法（二的step3），只不过没有一直换位置（一的step1）），最后才移到这段数字的最后。
所以法一法二本质上是相同的。
部分整理自慕课网“程序设计入门——C语言”课程，部分文字及图片来自原课程
如有错误，欢迎纠正
如有侵权，请联系删除
扫一扫
1万+
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
