协方差与相关系数

---

协方差

二维随机变量$(X，Y)$， $X$ 与 $Y$ 之间的协方差定义为：

$Cov(X,Y)=E[X-E(X)][Y-E(Y)]$

其中，$E(X)$为分量$X$的期望，$E(Y)$为分量$Y$的期望

协方差 $Cov(X,Y)$ 是描述随机变量是否相互关联的一个特征数。从协方差的定义可以看出，它是X的偏差 $[X-E(X)]$ 与Y的偏差 $[Y-E(Y)]$ 的乘积的数学期望。由于偏差可正可负，因此协方差也可正可负。

• 当协方差 $Cov(X,Y)>0$ 时，称X与Y正相关

• 当协方差 $Cov(X,Y)<0$ 时，称X与Y负相关

• 当协方差 $Cov(X,Y)=0$ 时，称X与Y不相关

但是，协方差仅能进行定性的分析，并不能进行定量的分析，比如身高体重之间的协方差为209.1，它们之间的相关性具体有多大呢，协方差并没有给出定量的判断标准。因此我们引出相关系数的概念。

---

相关系数

二维随机变量$(X，Y)$， $X$ 与 $Y$ 之间的相关系数定义为：

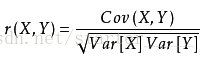
其中，$ Var(X) $为 $ X $ 的方差， $Var(Y) $ 为 $Y$ 的方差。

相关系数 $Corr(X,Y)$ 是描述随机变量相互关联程度的一个特征数。

• $Corr(X,Y)=-1$的时候，说明两个随机变量完全负相关，即满足 $Y=-aX+b，a>0$

• $0<|Corr(X,Y)|<1$ 的时候，说明两个随机变量具有一定程度的线性关系。

• $Corr(X,Y)=0$，表示X与Y没有线性关系

• $Corr(X,Y)=1$的时候，说明两个随机变量完全正相关，即满足 $Y=aX+b，a>0$（当两个随机变量相同，即$Corr(X,X$) ，肯定满足线性关系，此时，$Cov(X,X)=Var(X)$，容易得到 $Corr(X,Y)=1$）

---

##举例##

二维随机变量（身高X，体重Y）

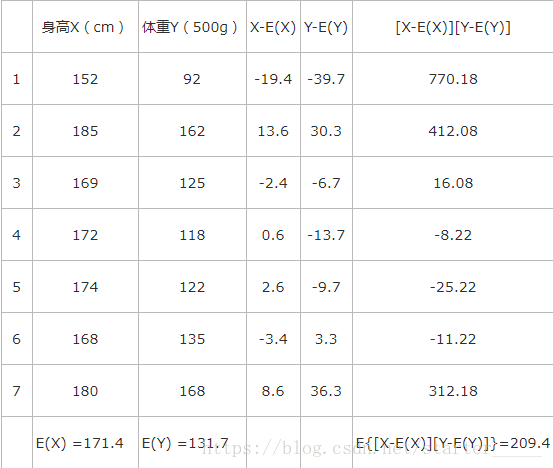
由此我们可以看到，身高和体重呈正相关。

此时，$Corr(X,Y)=209.4/(10.2\ast 24.4)=0.84$，故身高和体重的相关性为 $0.84$