一、AVL树定义
BST树的查找是通过二分查找的思想,可以很快着找到目的节点,查找所需的最大次数等同于二叉查找树的高度。
但是!!!如果在一棵BST树中要按顺序插入1、2、3、4、5、6这几个数,那么就会退化成一条链表,如图示:
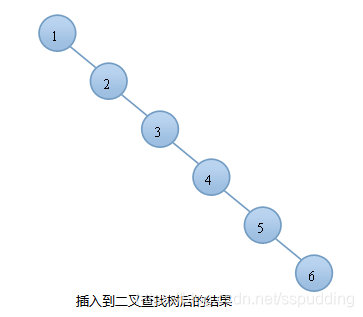
如果像上图那样的情况发生,BST 树在查找性能上就大打折扣,时间复杂度就退化成线性的了,增删查的时间复杂度就无法达到O(log2n)。
所以,就有了AVL树(平衡二叉树)。
什么是AVL树呢???
AVL树在BST数的基础上,加入了节点平衡的概念,平衡指的是任意一个节点的左子树和右子树的高度差不能超过1,那么这颗树就是一颗平衡树,否则就要通过既定规则的旋转操作,使节点重新达到平衡状态。
AVL树的特点:
- 首先是一棵BST树,具有BST树的所有特点
- 每个节点的左子树和右子树的高度差 <=1
/**
* AVL树节点定义
* @param <T>
*/
class AVLNode<T extends Comparable<T>>{
private T data;
private AVLNode<T> left;
private AVLNode<T> right;
private int height; // 记录当前节点的高度值
public AVLNode(T data, AVLNode<T> left, AVLNode<T> right, int height) {
this.data = data;
this.left = left;
this.right = right;
this.height = height;
}
public T getData() {
return data;
}
public void setData(T data) {
this.data = data;
}
public AVLNode<T> getLeft() {
return left;
}
public void setLeft(AVLNode<T> left) {
this.left = left;
}
public AVLNode<T> getRight() {
return right;
}
public void setRight(AVLNode<T> right) {
this.right = right;
}
public int getHeight() {
return height;
}
public void setHeight(int height) {
this.height = height;
}
}
/**
* AVL树的类定义
* @param <T>
*/
public class AVL<T extends Comparable<T>> {
private AVLNode<T> root; //指向根节点
public AVL(){
this.root = null;
}
/**
*获取node为根节点的树的高度
* @param node
* @return
*/
private int height(AVLNode<T> node){
return node == null ? 0 : node.getHeight();
}
/**
*返回当前节点左右子树的高度的最高值
* @param left
* @param right
* @return
*/
private int maxHeight(AVLNode<T> left,AVLNode<T> right) {
int l = height(left);
int r = height(right);
return l > r ? l : r;
}
}
二、旋转操作
那么像最开始的那种情况,在不破坏BST树特性的前提下,怎样将它变成AVL树呢???
要解决这个问题,我们就要先来了解AVL树的四种旋转操作了!!!
左—左型:右旋
这种情况是由左孩子的左子树引起的
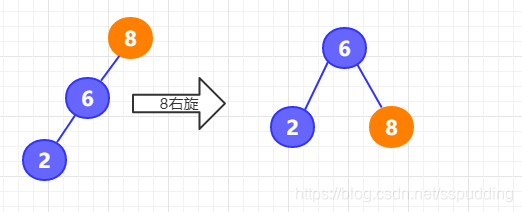
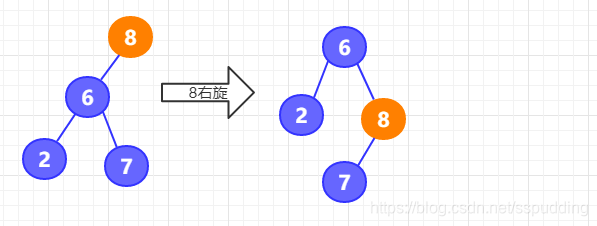
可以通过这个动图更清楚的看出来旋转过程

(动图源网络,侵删)
/**
* 以参数node为根节点进行右旋操作,把旋转后的树的根节点返回
* @param node
* @return
*/
private AVLNode<T> rightRotate(AVLNode<T> node){
AVLNode<T> child = node.getLeft(); //node节点的左孩子记为child
node.setLeft(child.getRight()); //将child的右孩子设为node节点的左孩子
child.setRight(node); //将child节点的右孩子设为node节点
//更新节点的高度值
//从下往上更新,因为父节点的高度值要依赖子节点进行计算
node.setHeight(maxHeight(node.getLeft(),node.getRight())+1); //先更新node的高度值
child.setHeight(maxHeight(child.getLeft(),child.getRight())+1); //再更新child的高度值
return child;
}
右—右型:左旋
由右孩子的右子树引起的
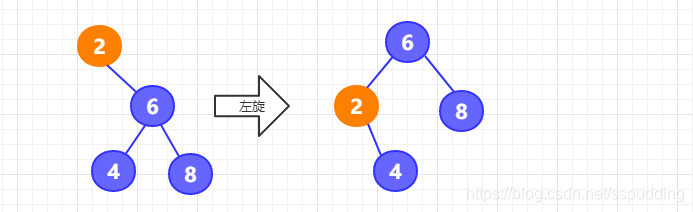
动图:
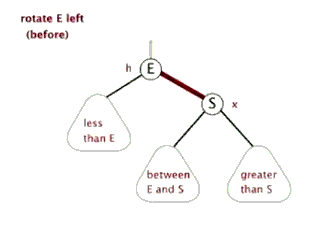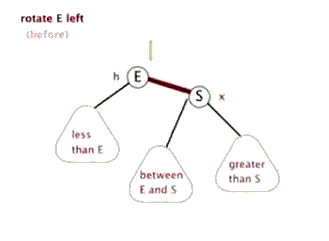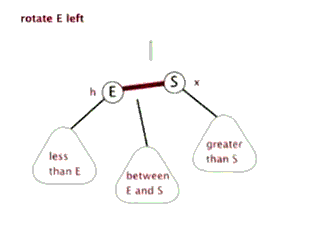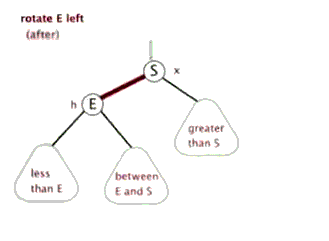
(动图源网络,侵删)
/**
* 以参数node为根节点进行左旋操作,把旋转后的树的根节点返回
* 需要更新node和child的高度
* @param node
* @return
*/
private AVLNode<T> leftRotate(AVLNode<T> node){
AVLNode<T> child = node.getRight();
node.setRight(child.getLeft()); //将child节点的左孩子设为node节点的右孩子
child.setLeft(node); //将child的左孩子设为node
//更新节点的高度
//从下往上更新,因为父节点的高度值要依赖于子节点进行计算
node.setHeight(maxHeight(node.getLeft(),node.getRight())+1);
child.setHeight(maxHeight(child.getLeft(),child.getRight())+1);
return child;
}
右—左型:先右旋再左旋
右孩子的左子树引起的 ,先以右孩子(child)为根节点进行右旋转,再以当前节点(root)为根节点进行左旋转
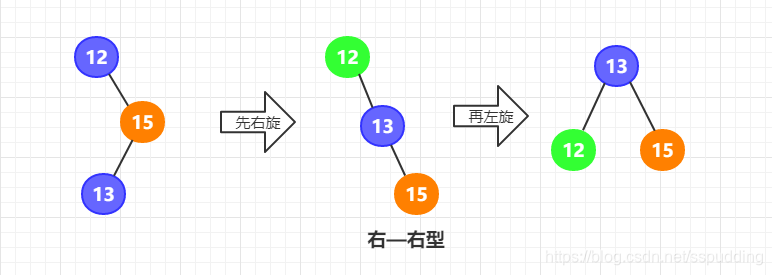
/**
* 以参数node为根节点进行右平衡操作,把旋转后的树的根节点返回
* (右-- 左旋转操作) 右孩子的左子树引起的
* 先以node的左孩子为根节点进行右旋转操作,再以node为根节点进行左旋转操作
* @param node
* @return
*/
private AVLNode<T> rightBalance(AVLNode<T> node){
node.setRight(rightRotate(node.getRight()));
return leftRotate(node);
}
左—右型:先左旋再右旋
左孩子的右子树引起的,先以当前节点的左孩子为根节点进行左旋,再以当前节点为根节点进行右旋
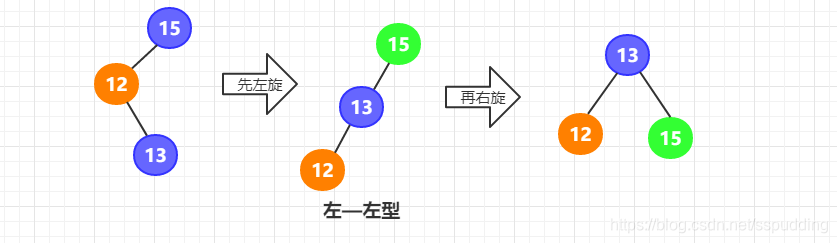
/**
* 以参数node为根节点进行左平衡操作,把旋转后的树的根节点返回
* ( 左-- 右旋转操作)左孩子的右子树引起的
* 先以node的左孩子为根节点进行左旋转操作,再以node为根节点进行右旋转操作
* @param node
* @return
*/
private AVLNode<T> leftBalance(AVLNode<T> node){
node.setLeft(leftRotate(node.getLeft()));
return rightRotate(node);
}
三、插入
/**
* 以参数root为起点,搜索一个合适的位置添加data,然后把子树的根节点返回
* @param root
* @param data
* @return
*/
private AVLNode<T> insert(AVLNode<T> root,T data){
if (root == null){
return new AVLNode<>(data,null,null,1);
}
if (root.getData().compareTo(data) > 0){
root.setLeft(insert(root.getLeft(),data));
//插入左子树 判断root节点是否失衡 #1
if (height(root.getLeft()) - height(root.getRight()) > 1){
if (height(root.getLeft().getLeft()) >= height(root.getLeft().getRight())){
//左孩子左子树太高 右旋转
root = rightRotate(root);
}else {
//左孩子右子树太高 左右旋转
root = leftBalance(root);
}
}
}else if (root.getData().compareTo(data) < 0){
root.setRight(insert(root.getRight(),data));
//判断root节点是否失衡 #2
if (height(root.getRight()) - height(root.getLeft()) > 1){
if (height(root.getRight().getRight()) >= height(root.getRight().getLeft())){
//右孩子的右子树太高
root = leftRotate(root);
}else {
//右孩子左子树太高
root = rightBalance(root);
}
}
}
//递归回溯过程中,更新节点的高度值 #3
root.setHeight(maxHeight(root.getLeft(),root.getRight())+1);
return root;
}
四、删除
/**
* 递归实现AVL删除函数
* @param root
* @param data
* @return
*/
private AVLNode<T> remove(AVLNode<T> root, T data) {
if (root == null) {
return null;
}
if (root.getData().compareTo(data) > 0) {
root.setLeft(remove(root.getLeft(), data));
if (height(root.getRight()) - height(root.getLeft()) > 1){
if (height(root.getRight().getRight()) >= height(root.getRight().getLeft())){
root = leftRotate(root);
}else {
root = rightBalance(root);
}
}
} else if (root.getData().compareTo(data) < 0) {
root.setRight(remove(root.getRight(), data));
if (height(root.getLeft()) - height(root.getRight()) > 1){
if (height(root.getLeft().getLeft()) >= height(root.getLeft().getRight())){
root = rightRotate(root);
}else {
root = leftBalance(root);
}
}
} else {
if (root.getLeft() != null && root.getRight() != null) {
//左右子树哪个高删除哪个,为了防止删除带来的旋转操作,提高效率
//递归删除前驱
if(height(root.getLeft()) >= height(root.getRight())){
//用前驱替换
AVLNode<T> pre = root.getLeft();
while (pre.getRight() != null){
pre = pre.getRight();
}
root.setData(pre.getData());
root.setLeft(remove(root.getLeft(),pre.getData())); //删除前驱
}else{
//用后继替换
AVLNode<T> post = root.getRight();
while (post.getLeft() != null){
post = post.getLeft();
}
root.setData(post.getData());
root.setRight(remove(root.getRight(),post.getData())); //删除后继
}
}else if (root.getLeft() != null){
return root.getLeft();
}else if (root.getRight() != null){
return root.getRight();
}else {
return null;
}
}
root.setHeight(maxHeight(root.getLeft(),root.getRight())+1);
return root;
}





















 282
282

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








