常规数据处理-优快云博客

常规数据处理

数据预处理的几个步骤
数据清洗

数据预处理的几个步骤

数据清洗
数据集成
数据变换
数据归约

数据清洗

处理缺失值的三种方法

直接删除该数据
重新收集数据
进行缺失值的填补

最常用方法利用平均数，中位数，众数代替缺失值

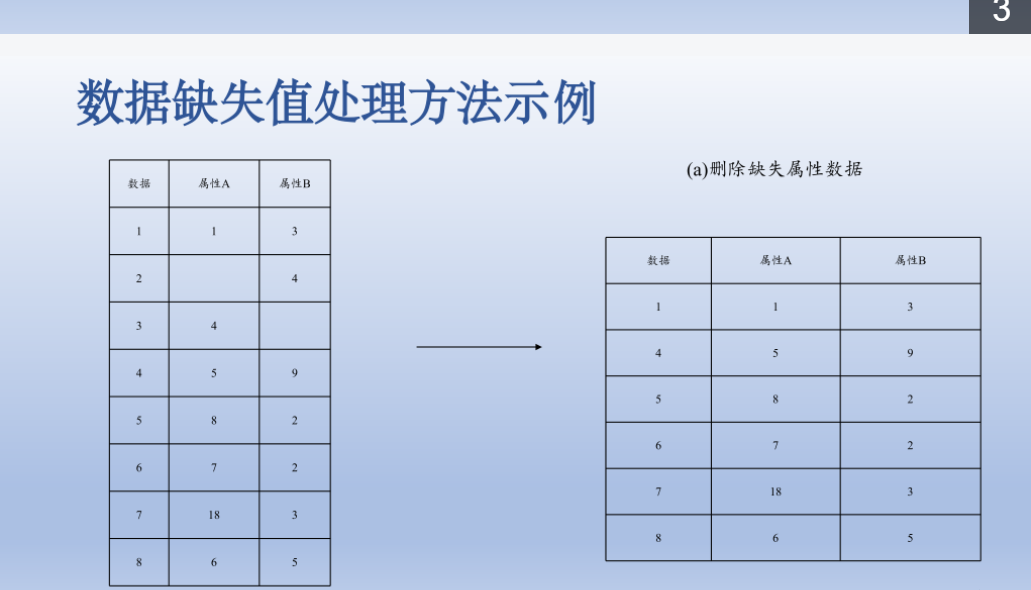
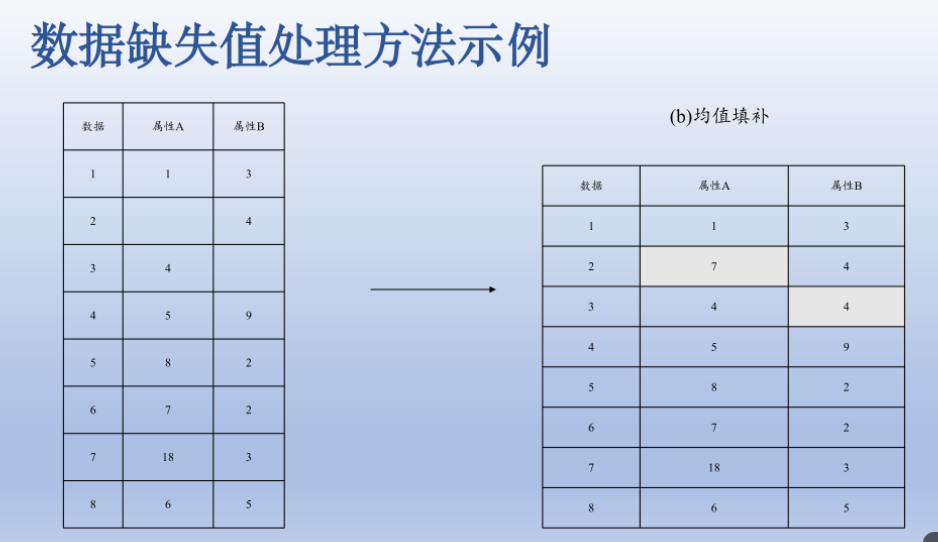
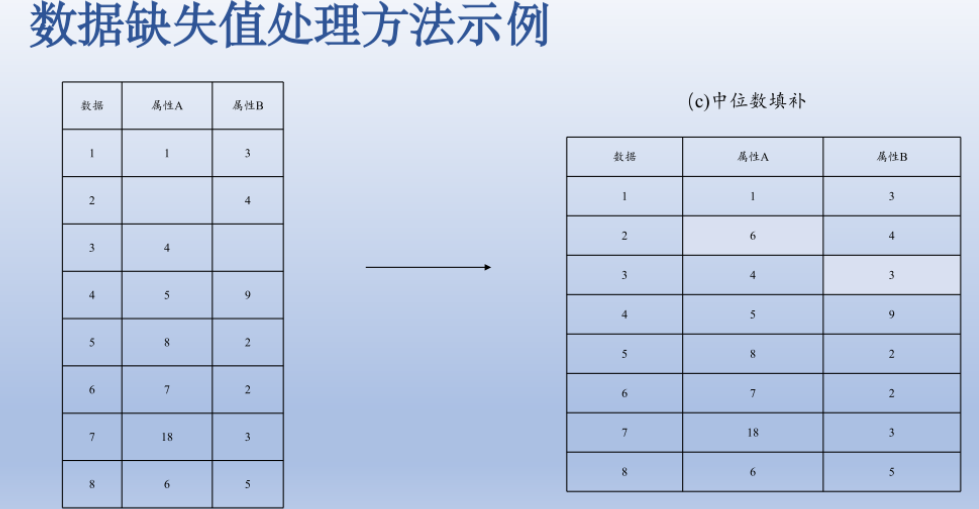
处理异常值和噪声数据

检测异常值

一般分为三个步骤

异常值检测
- 箱型图
- 简单统计量（观察极大极小值）
- 3原则
- 基于概率分布密度的检测
- 基于聚类的离群点的检测
异常值的筛选
异常值的处理

不会计算箱型图可参考箱型图详解

import pandas as pd
num = [1,2,3,4,5,6,7,8]
print (pd.DataFrame(num).describe())

这是一个Python脚本，使用了pandas库来对一组数字进行描述性统计分析。

第一行：import pandas as pd 这行代码导入了pandas库，并将其缩写为pd，以便在脚本中更方便地使用pandas的功能。

第二行：num = [1,2,3,4,5,6,7,8] 这行代码创建了一个名为num的列表，其中包含数字1到8。

第三行：print (pd.DataFrame(num).describe()) 这行代码将列表num转换为一个pandas的DataFrame，然后使用.describe()函数来生成描述性统计信息。最后，使用print函数将这些信息输出到屏幕上。

输出结果：

Unknown

       0
count  8.000000
mean   4.500000
std    2.291287
min    1.000000
25%    2.750000
50%    4.500000
75%    6.250000
max    8.000000

解释：

count：表示数据集中的观察值数量，这里是8。
mean：数据集的平均值，这里是4.5。
std：数据集的标准差，这里是2.291287。
min：数据集的最小值，这里是1。
25%：数据集的第一四分位数（25th percentile），这里是2.75。
50%：数据集的中位数（50th percentile），这里是4.5。
75%：数据集的第三四分位数（75th percentile），这里是6.25。
max：数据集的最大值，这里是8。

处理缺失值

处理异常值主要有四种方法：

删除：删除含有异常值的记录
视为缺失值：按照缺失值处理
平均值修正：可用前后两个观测值的平均值修正该异常值
不处理：忽略该异常值，或者不直接在具有异常值的数据集上进行数据挖掘

处理噪声数据方法

人工检测：人为地进行筛选
回归方法：发现两个或多个相关变量之间的变化模式，通过数据拟合一个函数来平滑数据
分箱方法（Binning）
- 通过相邻数据来确定最终值，包括等深分箱法，等宽分箱法，用户自定义区间法

分箱法

作为数据预处理的一部分，也被称为离散分箱或数据分段。其实分箱的概念其实很好理解，它的本质上就是把数据进行分组。

分箱就是把数据按特定的规则进行分组，实现数据的离散化，增强数据稳定性，减少过拟合风险。逻辑回归中进行分箱是非常必要的，其他树模型可以不进行分箱。

二、分箱原因在建立逻辑回归模型的过程中，基本都会对特征进行分箱的操作。

在这里插入图片描述

自定义

python实现分箱
等距分箱：pd.cut()
等频分箱：pd.qcut()

import pandas as pd

# 导入一列数据
df = pd.DataFrame({'年龄':[29,7,49,12,50,34,36,75,61,20,3,11]})

df['等距分箱'] = pd.cut(df['年龄'],4)    # 实现等距分箱，分为4个箱
df['等频分箱'] = pd.qcut(df['年龄'],4)    # 实现等频分箱，分为4个箱

df

这段文本是一段Python代码，用于演示如何使用pandas库进行数据分箱操作。具体来说，这段代码演示了两种分箱方法：等距分箱（equal-width binning）和等频分箱（equal-frequency binning）。

以下是对代码的逐行解释：

第一行：import pandas as pd

这行代码导入了pandas库，并将其别名为pd。pandas是一个广泛使用的Python库，用于数据处理和分析。

第二行：df = pd.DataFrame({'年龄':[29,7,49,12,50,34,36,75,61,20,3,11]})

这行代码创建了一个名为df的DataFrame（数据框），其中包含一列名为“年龄”的数据。DataFrame是pandas库中用于存储表格数据的一种数据结构，类似于电子表格或SQL表格。

第三行：df['等距分箱'] = pd.cut(df['年龄'], 4)

这行代码对“年龄”列的数据进行等距分箱，并将结果存储在名为“等距分箱”的新列中。pd.cut函数用于将连续数据离散化，分为指定数量的箱子（bin）。在这里，数据被分为4个箱子，每个箱子的范围是相等的。例如，如果年龄数据的最小值是3，最大值是75，那么每个箱子的范围可能是18岁（(75-3)/4=18）。

第四行：df['等频分箱'] = pd.qcut(df['年龄'], 4)

这行代码对“年龄”列的数据进行等频分箱，并将结果存储在名为“等频分箱”的新列中。pd.qcut函数也用于将连续数据离散化，但它确保每个箱子包含相同数量的观察值。也就是说，每个箱子的频率是相等的。例如，如果总共有12个观察值，那么每个箱子将包含3个观察值（12/4=3）。

最后，代码输出了分箱后的DataFrame df，其中包含原始的“年龄”列和两个新列：“等距分箱”和“等频分箱”。这两个新列分别表示等距分箱和等频分箱的结果。

运行结果：

在这里插入图片描述

结果解释

这是一份关于年龄分箱方法的表格数据，展示了两种不同的分箱方式——等距分箱和等频分箱的结果。表格中每一行代表一个数据点，列出了其年龄值以及在两种分箱方式下的分组区间。下面是对表格内容的详细解释：

表头解释
年龄：列出了具体的年龄数值。
等距分箱：将年龄范围均匀地划分为几个区间，每个区间的长度相等。
等频分箱：将年龄数据划分为几个区间，使得每个区间包含的观测值数量大致相等。
数据行解释

以第1行为例：

年龄：29岁。
等距分箱：被分在(21.0, 39.0]这个区间内。
等频分箱：被分在(11.75, 31.5]这个区间内。

以第7行为例：

年龄：75岁。
等距分箱：被分在(57.0, 75.0]这个区间内。
等频分箱：同样被分在(49.25, 75.0]这个区间内。
分箱方法的具体应用
等距分箱
区间划分：例如，21.0到39.0是一个区间，39.0到57.0是下一个区间，以此类推。每个区间的宽度都是固定的。
适用场景：当数据分布均匀时使用效果较好。
等频分箱
区间划分：例如，(11.75, 31.5]区间包含了多个年龄值，使得每个区间内包含的观测值数量大致相同。
适用场景：当数据分布不均匀或存在偏斜时使用，可以确保每个区间内有相近数量的观测值。

通过对比这两种分箱方法，可以看出它们在处理相同数据时的不同策略和效果。等距分箱更注重区间的宽度一致性，而等频分箱更关注每个区间内观测值数量的一致性。选择哪种方法取决于具体的数据特性和分析需求。

详细的分箱教程（有无监督性代码版）

均值平滑技术、边界值平滑技术

在这里插入图片描述

等深分箱法（均值平滑技术、边界值平滑技术）

import numpy as np
import math
# 要处理的数据
x = np.array([60,65,63,66,67,69,71,72,74,76,77,82,84,87,90])
#对数据排序
x.sort()
# 等深分箱法，深度为3
# 数据长度除以深度3，则为划分的数组行数
depth = x.reshape(int(x.size/3),3)
# 划分后的等深箱
depth
# 按平均值平滑，初始化mean_depth
mean_depth = np.full([5,3],0)
#等深分箱法、均值平滑技术
for i in range(0,5):
    for j in range(0,3):
        #第i行算数平均值
        mean_depth[i][j]=int(depth[i].mean())
# 按平均值平滑后的等深箱
mean_depth
# 定义等深箱每行左边界
edgeLeft = np.arange(5)
# 定义等深箱每行右边界
edgeRight = np.arange(5)
# 按边界值平滑，初始化edge_depth
edge_depth = np.full([5,3],0)
#等深分箱法、边界值平滑技术
#遍历等深箱行
for i in range(0,5):
    #第i行左边界
    edgeLeft[i]=depth[i][0];
    #第i行右边界
    edgeRight[i]=depth[i][-1];
    #遍历等深箱列
    for j in range(0,3):
        # 第一列，即左边界
        if(j==0):
            edge_depth[i][j]=depth[i][0]
        # 第3列（等深箱最后一列），即右边界
        if(j==2):
            edge_depth[i][j]=depth[i][2]
        else:
            # 判断距离左边界近还是距离右边界近
            if(math.pow((edgeLeft[i]-depth[i][j]),2)&gt;math.pow((edgeRight[i]-depth[i][j]),2)):
                edge_depth[i][j]=edgeRight[i]
            else:
                edge_depth[i][j]=edgeLeft[i]
# 按边界值平滑后的等深箱
edge_depth