紧凑型约瑟夫森混频器设计

约瑟夫森混频器的紧凑型设计：集总元件电路

J.-D.皮莱,1,2 E.弗鲁林,1 F.马莱,1,a)和B.于阿尔11皮埃尔·艾格朗实验室，巴黎高等师范学院‐ PSL研究大学，法国国家科学研究中心，巴黎第六大学‐索邦大学，巴黎第七大学‐索邦巴黎西岱大学， 法国巴黎勒蒙德街24号，75231巴黎五区2法国法兰西公学院，巴黎马塞尔·贝尔特洛广场11号， 75005巴黎
（2015年3月27日收到；2015年5月19日接受；2015年6月3日在线发表） 我们提出了一种紧凑且高效的约瑟夫森混频器设计，该超导电路在微波频率下实现三波混频， 在增益、带宽和动态范围方面表现优异。在一个全部基于集总元件的电路中，通过直接耦合 端口，我们在50MHz的带宽内实现了20dB功率增益的非简并放大。该混合器的量子效率约 为70%，其饱和功率达到 112 dBm。VC 2015作者。除另有注明外，所有文章内容均采 用知识共享署名3.0未本地化许可授权。。[http://dx.doi.org/10.1063/1.4922188]

由于超导电路的发展，微波信号的模拟处理最近已 进入量子区域。基于约瑟夫森结提供的非线性而构建的 量子极限放大器已在多种设计中实现。1–20非简并三波 混频这一关键操作由约瑟夫森环形调制器（JRM）实现， 该器件是由四个相同的约瑟夫森结构成的环。21,22该元 件是多种能够生成和操控量子微波模式工具的核心，例 如相位保持放大器、23–25非局域纠缠源、26频率转换 器、27量子存储器、28或环行器。29,30在之前所有约瑟 夫森混频器的实现中，JRM均被嵌入两个分布或集总谐 振器的交叉处，这会对带宽和动态范围造成限制，可能 对量子操作产生不利影响。本文讨论了该限制的来源以 及如何优化约瑟夫森混频器的性能指标。这些思想在一 个实验中得以实践，其中相位保持放大器完全由一个与 集总板电容器并联的JRM构成。与之前的实现相比，我 们报告其动态带宽提高了近一个数量级，在20dB的功率 增益下达到50MHz，同时保持动态范围高达112 dBm。

在约瑟夫森混频器中，JRM通过最低阶耦合项H mix ¼ EJsinðU=4u0 Þuaubup耦合三个独立的磁通量ua; ub;和up （图1(a)），其中EJ 为每个结的约瑟夫森能 量，u 0 ¼ h=2e为约化磁通量子，U为穿过环的磁通量。 通过将环嵌入谐振电路（图1(b)）实现三波混频，使得 每个磁通量可表示为u k / ð^k þ^k † Þ，其中^k是具有 特征阻抗Z k 和谐振频率f k 的微波模式的正则湮灭算符。 尽管约瑟夫森混频器有多种使用方式，21–23 , 25–29我们将 重点关注 这里讨论放大区域，以便在具体情况下描述性能指标。 发送到a和b模式的信号通过以频率fa þfb驱动p模式远离 共振，在反射中以相位保持的方式被放大：21在量子微 波信号的模拟处理中，有三个主要技术指标至关重要。 首先，放大器的功率增益G必须足够大，使得放大器输 入端的量子噪声主导检测装置中的所有其他噪声源。通 常情况下，如果使用低温HEMT作为第二级放大，则 20分贝已足够。31其次，量子信号的时间关联应由研究 系统主导，而不是由约瑟夫森混频器主导。这要求动态 频率带宽C尽可能大。最后，不影响增益超过1dB的最大 输入功率Pmax in必须足够大，以避免对量子信号的幅度造 成任何限制。

针对实际放大器优化这三个参数一直是近年来在不 同几何结构中开展的实验工作的核心。最近，简并约瑟 夫森参量放大器在全集总元件设计中实现了超过 700MHz带宽的15dB以上增益，而在氮化钛行波参量放 大器中已报道实现了GHz带宽下的15dB增益。 约瑟夫森混频器参数的约束与其简并型器件约瑟夫森参 量放大器的约束起因相似，但存在一些差异。首先，由 于三波混频项Hmix中的小磁通up假设，泵浦模式p中存 储的能量存在一个上限。因此，为了使泵浦功率能够达 到参量振荡起始点（在此处产生大增益G），必须确保22 paQapbQb > N; (1) 其中N是取决于混合器具体几何结构32的数值，后续将 使用N¼ 8。在此表达式中，Qk 是模式k的品质因数， 定义为Qk ¼f k =Ck ，其中C k 是共振带宽。 a ) 通讯作者。电子邮箱：francois.mallet@lpa.ens.fr 0003‐6951/2015/106(22)/222603/5 V C 作者2015 106,222603‐1 应用物理快报106,222603(2015)

JRM约瑟夫森结在k模式中的参与比pk量化了该模式中 的总能量实际存储在JRM结上的比例。其次，在三波混 频项Hmix中，小磁通ua;b假设对放大信号的功率谱密度 存在一个上限。实际上，输入信号功率Pin和真空噪声都 不应被放大超过约瑟夫森能量EJ的一个分数。对于大增 益情况，此条件可近似为 pkG（Pin /（2pCk） ＋ hf ）N0 < E J ; (2) 其中N0是数量级为1的数，E J 是约瑟夫森能量EJ ¼u 2 0 = LJ。上述约束条件(1)和(2)表明，对于给定的增益G，若 要同时增加Pmax in 和C，则需要提高参与比pk 以及约瑟夫 森结能量E J 。然而，这两个参数通常是相关的，因为 JRM中单个结的约瑟夫森电感随EJ的增大而减小，即 L J ¼ u2 0 /EJ 。当谐振器的所有电感部分均来自约瑟夫森 结本身时（图1(c)），无论E J 取何值，都可以方便地设 定pk ¼ 1。 实际上，由于电路的有限尺寸，会产生寄生几何电感。 对于额外的电感Lk ex 与结串联时，得到pk ¼ LJ/（LJ ＋Lk ex）（图1(d)）。在参数 相空间中以图形方式表示约束条件(1,2)具有启发性。在 图1(e)中，阴影区域针对Lex的两个不同值，划定了典型 量子极限放大器在频率f ¼ 7 GHz下工作、具有20dB功 率增益和饱和输入功率Pmax in ¼ 110 dBm时，品质因数 Q和约瑟夫森电感LJ的允许取值范围。为清晰起见，图 中将a和b模式设置为相同参数。如图所示，只有降低Lex 才能获得更低的Q（更大的带宽）。相反，图1(f)显示了 对于几种期望的品质因数Q，最大允许附加电感Lmax ex随饱 和功率Pmax in变化的关系。根据这些曲线，可以推导出给 定带宽下可使用的最大附加电感Lmax ex 。如果Lex来源于某 些导线的几何电感，则其长度约为Lex/l0,，该值表示在图 1(f)右侧坐标轴上。基于这些考虑，还可确定约瑟夫森混 频器为确保特定带宽所需的最大空间延展。

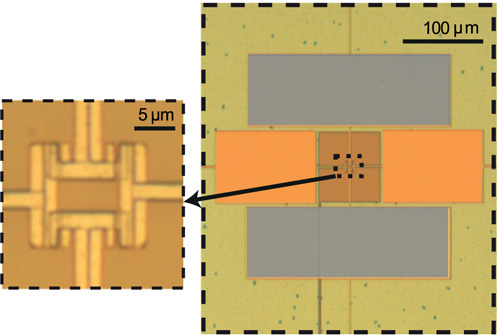
图1(c)所示设计的实现如图2所示。a和b模式谐振 器由JRM构成，该JRM并联了一个平板电容器十字结构。 该电路被制造在一片500μm厚的Si芯片上，其顶部覆盖 有300nm的SiO2层。第一步，使用标准电子束光刻工艺 在所有平板电容器下方制作一个Ti(5nm)/Al(30nm)的 公共对电极（图2(b)中为深黄色）。该电极分布在电路 其余部分下方的整个表面，但中心孔和一条细条区域 （图2(b)中为棕色）除外，以便进行磁通偏置 消除了迈斯纳效应带来的约束后的电路。然后通过等离 子体增强化学气相沉积在整个芯片上覆盖200纳米非晶 介电氮化硅。最后，通过双角度沉积100纳米和120纳米 铝并中间进行氧化处理，制备出电容器的第二金属极板 （a谐振器面积为285lm 86 lm，b谐振器面积为140 lm 86 lm）以及约瑟夫森结（面积为4.2lm 1 lm） （图2(c)）。该电路随后被放置在一个铜盒内，铜盒再 封装于一个锚定在稀释制冷机基温端（Tdil ’ 50 mK） 的高导磁合金磁屏蔽盒中。两个 180混合耦合器分别 通过其D端口连接差分a和b模式，并通过其中一个R端 口连接泵浦模式c。谐振器的特性阻抗小于10X，并直接 电连接到器件的50X端口，以最大化带宽，仅受限于阻 抗失配。由于差分模式与输入/输出端口之间存在强耦合， 增益对阻抗的频率依赖性较为敏感。17为了单独探测约 瑟夫森混频器的特性而不必精心设计环境阻抗，我们在 混合耦合器的D端口连接了一个6dB衰减器。6dB衰减 器的影响可在图3(b)中混频器的频谱响应上观察到。通 过一个线圈施加电流Icoil，可调控穿过JRM环路的磁通， 从而调节Hmix中的混频项。 磁通偏置的影响也可以在谐振频率fa和fb上观察到 （图3(a)），它们以滞后方式依赖于磁通，周期为4/0。21 这种滞后行为可以通过在JRM中插入额外的电感来消除， 从而扩展放大器的静态带宽。25然而，这会降低参与比， 而我们旨在最大化参与比，并且当动态带宽较大时，这种 方法的效果也会减弱。在此器件中，我们观察到Icoil对频 率的依赖性并非完全周期性。Uext对Icoil的这种非线性依 赖可能源于埋在氮化硅下方的大尺寸超导电容器极板中的 涡旋动力学。对于每个谐振频率，都可以测量其品质因数 （图3(a)插图）。这种依赖关系可用于建立描述约瑟夫森 混频器的定量模型。在这个基于图1(d)的详细模型中，考 虑了与电容Cres串联的寄生电感Lstray。首先通过对整个器 件进行完整的三维微波模拟，可以估算出几何电参数C a stray ＋ La ex ¼ 130 pH和Cb res ¼ 6 pF、Lb stray ＋ Lb ex ¼ 85 pH。然后通过拟合LJ ¼ 90 pH，得到f ðf itÞ a ¼ 6: 95GHz和f（f it） b¼ 5:7GHz，这与在Uext ¼ 0下测得的谐 振频率接近（图3(a)）。由此可估算参与比为pa ¼ 25% 和pb ¼ 35%。需要注意的是，通过直接拟合谐振频率的 磁通依赖性也可获得类似的参与比值（见参考文献28的 补充材料）。最后，可以拟合寄生电感以最好地复现参考 文献35中推导出的Q(f)曲线，并得到La stray ¼ 75 pH、L b stray ¼ 51 pH。约瑟夫森混频器可用作放大器，方法是将 磁通/1设置略低于2/0 ¼h/e，并在频率fp ¼ 12:26GHz （接近fa ＋fares ¼ 3）处驱动c泵浦模式。21增益定义为泵 浦开启与关闭时反射功率的比值，在固定磁通/1下，针对 不同的泵浦功率Pp，测量了两个放大器端口的反射增益 随频率的变化（图3(b)）。随着泵浦功率逐渐接近参量振 荡阈值，两个端口的增益均增加至30dB。相反，工作带 宽则减小。该曲线表明在20分贝时带宽为50MHz，比之 前实现的约瑟夫森混频器高出一个数量级。23–25

约瑟夫森混频器可用作放大器，方法是将磁通/1设置略低于2/0 ¼h/e，并在频率fp ¼ 12:26GHz （接近fa ＋fares ¼ 3）处驱动c泵浦模式。21增益定义为泵 浦开启与关闭时反射功率的比值，在固定磁通/1下，针对 不同的泵浦功率Pp，测量了两个放大器端口的反射增益 随频率的变化（图3(b)）。随着泵浦功率逐渐接近参量振 荡阈值，两个端口的增益均增加至30dB。相反，工作带 宽则减小。该曲线表明在20分贝时带宽为50MHz，比之 前实现的约瑟夫森混频器高出一个数量级。23–25

通过放大a和b模式中的零点涨落来评估放大器的附 加噪声。频谱分析仪测量来自aout和bout的功率谱密度随 Pp的变化关系。没有信号输入到ain 和bin 中。放大器在开 启和关闭状态下的功率谱密度之差由下式给出
S ON S O FF ¼ G LNA hf G（Sadd ＋ 1）; (3) 其中G是放大器的增益，G LNA 是输出线路的总增益。 这里假设模式处于真空态，且G 1。在这种情况下， 附加噪声S add 可与混合器的量子效率g联系起来，关系 为26：S add ¼ （1 g）/2g。因此，确定g需要分别测量放大 器增益G（如图3所示）以及对衰减和增益进行精细校准 连接混合器与探测器的输入和输出线路。我们通过测量 发送到ain和bin的功率变化所引起的频率偏移来获得该 校准结果。通过与图1(d)所示电路35的数值计算结果进 行比较，可精确校准从ain到混合器之间的输入线路衰 减。当泵浦关闭时，约瑟夫森混频器与aout之间的增益 GLNA则由ain与aout之间的总传输系数推导得出。需要注 意的是，在改变泵浦功率时，图3(b)中的增益测量也显 示出明显的频率偏移，这是由于与Ppa†a和Ppb†b成正比 的高阶交叉克尔36项所致。图4(a)展示了测得的g随增益 G的变化关系。结果显示效率为0.7，与独立测量结果35 一致，在增益超过33dB之前保持该效率；当增益超过 33dB后，放大器进入参量振荡区域，此时g约为0.2。

放大器的最后一个重要指标是其动态范围，该范围 由放大器的1dB压缩点Pmax in表征。在约瑟夫森参量器件 （如约瑟夫森混频器）中，这种饱和现象可能由泵浦耗 尽（即增益过大导致泵浦无法快速补充以供给放大器） 引起，也可能由于光子数达到一定程度，使得高阶非线 性效应不可忽略所致。利用端口b上方输入功率Pin的校 准结果，我们使用矢量网络分析仪测量了在6.76GHz （中心4(b)）时输出功率Pout随输入功率Pin的变化关系 （图 频率为G ¼ 20 dB）时，针对不同泵浦功率的情况，参 考文献22。在低输入功率Pin< 120dBm下，增益G随 泵浦功率Pp的增加从0上升至25dB，且不依赖于Pin。当 泵浦功率对应低输入功率下的G ¼ 20 dB增益时，放大器 在低功率下表现为线性，直到在JRM输入端达到1dB压 缩点，即 112 dBm。在6.76GHz和50MHz带宽下， 该功率对应4.5个光子每带宽。超过此阈值后，增益下降 并最终饱和。该动态范围足够大，不仅可用于量子比特 读出24还可用于放大真空压缩态。26

总之，我们讨论了一种用于约瑟夫森混频器的高效 且紧凑的设计，并应用这些原理实现了保持相位的量子 噪声极限放大。该器件在距离量子噪声极限仅0.4个光子 的情况下实现高达30dB的增益，饱和功率为 112 dBm，相当于每带宽4.5个光子，这对于量子信号的模 拟信息处理、定向放大以及片上环行器具有良好的前景。 30这些参数并未限制混频器的动态带宽，在G¼ 20 dB时 动态带宽可达50MHz。此类器件适用于超导量子比特 的快速操作，这对于提升量子反馈效率、38,39多路复用多 个量子比特37或更广泛的量子纠错方案至关重要。