基于预测切换的数据估计

无线传感器网络中基于预测切换机制的数据估计

1 引言

无线传感器网络（WSN）由密集部署的传感器节点组成，这些节点被布置在某一地理区域（例如森林、水下、农田等），用于从事件中提取信息。传感器节点的任务是从地理区域（或环境）中测量事件特征，如温度、湿度或含水量等。传感器节点是基于事件的系统，在 Vuran 等人（2004）的研究中被提出，能够在空间和时间上从环境中收集信息。传感器节点持续地在空间和时间上观测物理数据，并最终将其传输至汇聚节点。在图1中，汇点直接从网络中的传感器节点接收所传输的数据。传感器节点具备协作特性，能够协同收集数据。

这种协作式的信息采集方式使得网络中获取准确信息的程度更高。此外，协作式的信息交换带来了传感器观测之间的时空相关性，这一点在 Vuran 等人（2004）、Chen 等人（2010）中均有考虑，也是无线传感器网络的一个显著特征。由于传感器节点在网络中的密集度较高，根据 Vuran 等人（2004）的提出，传感器观测在空间和时间上具有高度相关性。这导致可以在网络中选择较少数量的节点来向汇点传输数据。空间相关数据为在网络中跨空间和时间选择最优传感器节点提供了显著优势，这一点在 Karjee 和 Jamadagni（2011）中有所论述。

Sink
Node 1
Node 2
Node 3 Node 4
Node m
. .
. .

汇聚节点存储空间相关数据，并使用Vuran等人（2004）、Cai 等人（2008）、Li 等人（2006）和Karjee 等人（2014）中考虑的失真（或精度）水平对网络进行数据估计。Karjee 等人（2014）以及Karjee和Jamadagni（2011，2012）提出了数据估计模型，能够在网络中以显著的失真水平来估计准确的信息。在此失真因子（DF）下，选择最优传感器节点，这些节点足以达到网络中所有传感器节点所实现的相同失真水平。因此，大多数研究工作都集中在网络中失真水平下寻找最优传感器节点。在本文中，我们旨在估计最优数据从汇点在此失真因子下收集的原始数据。失真因子在汇聚节点进行数据估计。由于汇聚节点以固定时间间隔持续接收来自传感器节点的数据，经过一定时间后，汇聚节点处已收集到大量数据。因此，汇聚节点需要存储这些海量数据并对其进行网络处理。为解决在汇聚节点存储和处理如此巨大数据的问题，我们设计了如图2所示的ODTE算法。ODTE算法执行两项操作：数据跟踪与数据估计。

数据估计 （最优数据存储）
数据跟踪 处理数据
汇聚节点
由m个传感器节点收集的数据

•数据跟踪：

在无线传感器网络中，最大的挑战之一是在汇聚节点上处理高维（海量）数据的存储和处理速度。因此，本文利用Balzano等人（2010）、He等（2011）和Hage与Kleinsteuber（2014）研究的适当子空间方法，将高维数据在汇聚节点处近似为低维数据子空间。低维子空间方法依赖于全维数据，并用于子空间跟踪。最近，Balzano等人（2010）、He等（2011）和 Hage与Kleinsteuber（2014）提出的在线子空间跟踪算法被开发用于实时视频的背景与前景分离跟踪。此外， Michel等（2000）提出的低秩子空间模型也应用于医学成像应用中。据我们所知，目前尚无研究针对无线传感器网络中传感器数据的高效在线子空间跟踪。在无线传感器网络中，汇聚节点以固定时间间隔存储数据。因此，经过一定时间后，汇聚节点将积累大量数据，这使得在网络中处理如此巨大的数据量变得困难。受用于将高维数据近似为低维子空间的子空间跟踪方法的启发，我们提出了一种数据跟踪机制，能够处理汇聚节点收集的大 量数据。该机制能够学习数据模式，并且相比 Karjee和Jamadagni（2013）提出的传统模型，可以更快速地进行处理。在线数据跟踪在处理

在无线传感器网络中高效地处理大规模（高维）数据。因此，以高效方式处理高维数据是解决无线传感器网络中大数据问题的另一种方法Vodelet等（2014）。

•数据估计：

由于传感器节点持续向汇聚节点传输数据，随着时间的推移，数据量不断增长，同时汇聚节点需要存储这些海量数据。这会增加网络中的数据冗余，因为汇聚节点收集的数据具有空间相关性。在汇聚节点上处理所有接收到的数据并非必要，而可以在失真因子的约束下估计出最优数据，从而充分反映这些海量数据的信息。这可以减少数据冗余，并节省汇聚节点的存储容量。据作者所知，ODTE算法是首个为无线传感器网络（WSNs）开发的能够高效实现在线数据跟踪的算法，可从汇聚节点收集的大量数据中度量出最优数据。

由于传感器节点在固定时间间隔内向汇聚节点传输数据，导致网络中的数据流量增加，从而产生较高的传输开销。为解决这一问题，Santini和罗默（2006）研究了数据缩减策略，该策略通过从汇聚节点接收到的所有数据中选择部分观测数据，在降低网络通信开销方面发挥着关键作用。近年来，数据缩减在无线传感器网络领域受到了广泛关注。传感器节点可在空间域（Guestrin 等人 (2004)）、时间域（Jain 和 Chang (2004)）或二者同时进行（Deshpande 等人 (2004)）提取观测数据。Karjee和Jamadagni（2013）提出的基于时空相关性的数据缩减方法也强调了降低网络通信开销的重要性。在Ali 等 (2008a)中，已在汇聚节点开发了用于网络数据预测的估计技术。受Karjee和Jamadagni（2013）的启发，我们提出了基于数据缩减策略的数据预测系统（DPS）模型。DPS模型具备学习与跟踪能力，可有效降低网络中的通信开销。它采用自适应学习算法，既应用于汇聚节点，也应用于邻近传感器节点，并在汇聚节点实施Santini和罗默（2006）提出的联合预测方案，以捕捉时空相关数据。由于汇聚节点收集的是空间相关的高维数据，因此有必要利用数据跟踪将这些高维数据降维（或逼近）至低维子空间。据作者所知，这是首次将DPS模型用于将高维数据分解为低秩矩阵以实现子空间跟踪，而传统的预测模型如Santini和罗默（2006）、Karjee和Jamadagni（2013）、阿里等人（2008b）在无线传感器网络的数据缩减策略中尚未涉及此能力。相比传统方法，DPS能够更高效地跟踪数据。本文重点构建DPS的理论模型，该模型是对Karjee和 Jamadagni（2013）中STDP模型的改进和扩展版本。Heinzelman 等人 (2002)、Le Borgne 等人 (2007)、 王等人 (2007) 提出的能耗模型也被集成到DPS中。最后，将DPS模型与STDP模型在网络中的能耗方面进行了比较。本文的主要贡献是：

• 首先，我们开发了ODTE算法，该算法在汇聚节点进行数据跟踪并估计最优数据，同时保持期望的失真因子
• 其次，通过在阈值限制内应用切换机制，开发了 DPS模型以控制网络中的数据传输。

本文的其余部分组织如下：在第2节中，我们给出问题定义。在第3节中，对网络中的数据跟踪与数据估计进行分析。在第4节中，应用数据预测机制来控制数据传输。在第5节中，进行仿真与验证。最后，在第6节中得出结论。

符号说明 ：矩阵用粗体大写字母表示，如 U、 K；向量用粗体小写字母表示，例如 v、 z等；标量用小写或大写字母表示，如 l、 E；期望可表示为 E，实空间用 Rm、 Rn表示。ODTE算法中使用的全局统计信息，即协方差矩阵和数据相关向量，分别用 RUU和 RUy表示。类似地，在DPS模型中，全局统计信息可用 RV V表示协方差矩阵， RUV表示相关向量。

2 问题描述

2.1 以高效的方式处理和存储数据

在无线传感器网络中，汇聚节点利用Karjee和 Jamadagni（2011，2012）所考虑的最小均方误差（ MMSE），在已知环境数据统计信息（如方差、协方差等）的先验条件下，对传感器节点的数据进行估计。由于在先验条件下数据统计信息已知，汇聚节点可以轻松地对任意网络进行数据估计。但在没有数据先验知识的情况下对网络进行数据估计，是无线传感器网络中的一项挑战性任务。在这种情况下，如Karjee和Jamadagni（2013）所述，数据统计的先验信息未知，且传感器节点以固定时间间隔动态感知连续数据。由于传感器节点在较长时间内持续感知数据，汇聚节点接收到的数据量巨大。因此，处理和存储汇聚节点接收到的如此巨大的数据变得困难。为解决此问题，在汇聚节点进行在线数据跟踪以捕获连续数据至关重要。利用降维技术的在线数据跟踪有助于在无线传感器网络中以最优方式处理和估计海量数据。针对在汇聚节点高效存储海量数据并及时处理的问题，我们提出ODTE算法，该算法可在网络中实现连续数据流的在线跟踪，并以最优方式估计数据，具体如下：

在线数据跟踪：

我们考虑一种无线传感器网络场景，其中每个感知节点向其传输连续的数据样本流

汇聚节点。在无线传感器网络中，我们假设有两个信道：观测信道和通信信道。观测信道描述了环境中原始数据（例如温度）如何被网络中的每个传感器节点提取。此外，我们假设在观测信道中，每个传感器节点对原始数据的提取是相互独立的。对于从每个传感器节点到汇聚节点的数据传输，我们在通信信道中采用Vuran等人（2004）所考虑的加性高斯白噪声（AWGN）信道。汇聚节点在时间间隔 t= 1,2,…, T存储数据向量序列 v1, v2,…, vn，其中包含m个传感器节点对感知数据的n次观测。我们的目标是找到由 S(t)在时间间隔t上给出的 Rm的d维子空间。这意味着在每一个时间间隔t，我们在汇聚节点观测到一个列向量 vt ∈ S(t)。我们将 Rm的d维子空间用格拉斯曼流形表示为 Gr(m, d)，如Balzano等人（2010）、Edelman等人（1998）所述。因此， S(t) ∈ Gr(m, d) 可以表示为 m × d矩阵 Ut，其列向量是正交归一化的，并张成子空间 S(t)，其中 d ≤ m。在汇聚节点，我们假设观测到的数据向量 vt位于时间间隔 t由 U张成的子空间内

$$
vt= Utα+ ςt+ γt, (1)
$$

其中 U是一个 m × d矩阵，α是一个 d × 1系数向量，ςt是环境的高斯白噪声， γt是系统噪声。我们从由 Ut张成的子空间S(t)中构建一个估计加权向量 y，用于跟踪给定的观测向量 vt。

$$
y= arg min_α ||(vt − Utα)||2 (2)
$$

数据估计：

一旦完成数据跟踪，汇聚节点便开始对网络进行数据估计。数据估计定义为网络中提取的测量值与其实际传感器数据的准确程度。对于数据估计， ODTE算法使用代价函数 J(w∗)计算失真因子（DF）。失真因子（DF）是用于归一化代价函数，从而在汇聚节点获得数据估计的一个因子。为了评估J(w∗)，我们采用方程(2)以及受最小均方滤波器（Sayed, 2008）启发的权重向量w ∗。我们构建 J(w ∗ )以最小化 w ∗，使得数据估计尽可能接近其实际观测值 vt。

$$
J(w ∗ )= min_{w∗} ||vt − UtU T t w ∗||2. (3)
$$

2.2 通过预测模型减少传输开销

随着时间的推移，传感器节点到汇聚节点的数据传输量会在网络中产生拥塞。为了减少网络流量并控制从传感器节点到汇聚节点的数据传输，我们开发了称为DPS的预测模型。在数据缩减策略下，DPS机制更适用于降低网络中的通信开销。在预测机制中，传感器节点无需始终向汇聚节点发送数据，而是采用Karjee和 Jamadagni提出的切换机制。(2013)用于在汇聚节点上传输数据。一旦传感器节点采用该预测机制，便停止向汇点传输数据，而汇点则开始为网络预测数据。DPS大致分为两类：列向数据预测系统 (C‐DPS)和逐行数据预测系统(R‐DPS)。在C‐DPS模型中，在每个时间间隔 t观测一个列向量 vt，以跟踪汇点处的数据。由于每次跟踪的是 m × 1维的列向量 vt，因此我们将其视为列向的。列向数据 vt在 Gr(m, d)格拉斯曼流形下进行跟踪，以预测网络中的数据。在R‐DPS中，汇点以固定时间间隔跟踪一组包含n个观测数据的行。因此，这组包含n个观测数据的行在 Gr(n, d)格拉斯曼流形下进行跟踪，且由汇点负责为网络预测数据。

2.3 与先前工作的关系

本文旨在解决无线传感器网络应用中在线数据跟踪的问题，以将近似高维数据转换为低维数据矩阵。我们的工作不同于Hage和Kleinsteuber（2014）将数据分解为低秩矩阵的方法，也不同于Balzano等人（2010）、 He等（2011）、Seidel等人（2014）提出的传统鲁棒子空间跟踪方法，后者在时间间隔 t内追踪列向量 vt，以从协方差矩阵 E[vtv T t]计算数据相关矩阵，从而提取网络中传感器节点间的时空特征。我们尝试将鲁棒在线子空间跟踪方法应用于无线传感器网络应用，而非传统方法中用于视频应用的场景，以将近似高维数据映射到低维子空间。在完成数据跟踪后，我们进一步希望在汇聚节点处估计最优数据。最优数据估计对于在网络中存储海量数据具有重要意义。然而，我们在问题描述方面与以往研究不同，以往研究如Vuran等人（2004）、 Cai 等人（2008）、Li 等人（2006）、Karjee 等人 （2014）以及Karjee和Jamadagni（2011，2012）均基于失真因子（DF）进行最优数据估计。这些研究主要通过寻找网络中的最优传感器节点集合，以维持期望的失真因子。而我们的方法则是利用该失真因子在无线传感器网络中寻找数据存储的最优解。此外，Luo等人 （2010）也提出了不同的问题描述，即通过压缩感知 （CS）方案（包括非CS、纯CS和混合CS）在网络层寻找数据聚合最优解的下界，以提高吞吐量。但在我们的工作中，我们致力于在物理层通过确定失真因子来获得估计数据的最优解。由于无线传感器网络中的数据具有空间相关性，我们利用时空数据在物理层求解最优方案，弥补了Luo等人（2010）所提出方法在此方面的不足。因此，我们将时空数据、数据跟踪与数据估计相结合，提出了一种ODTE算法。

朴等人（2014）提出了利用低秩矩阵逼近的时空数据相关方法，有效降低了能耗，从而延长了无线传感器网络寿命。但在我们的工作中，我们利用时空数据和低秩近似开发算法，在数据处理、数据存储和数据预测方面具有高效性，从而减少了网络中的通信开销。此外，我们致力于开发一种称为C‐DPS的数据预测模型，该模型利用数据跟踪以及在时间间隔 t内由 Ut张成的子空间。据作者所知，这是首次从由 Ut张成的子空间中构建数据预测模型，用于将高维数据分解为低秩矩阵，而这一点在桑蒂尼和罗默（2006）、Karjee和Jamadagni （2013）以及阿里等人（2008b）提出的传统方法中尚属欠缺。C‐DPS模型在数据跟踪方面可能比Karjee和 Jamadagni（2013）先前的工作更高效。此外，我们还开发了另一种数据预测模型，即R‐DPS模型，它是Karjee和 Jamadagni（2013）所提出工作的扩展。与之前的工作不同，我们采用最小均方滤波器和归一化最小均方滤波器传输单比特数据，而不是向汇聚节点传输包含 n个观测样本的数据块。因此，C‐DPS和R‐DPS模型均可实现对数据的快速跟踪，从而提高预测模型的效率。

3 在线数据跟踪与估计

在本节中，我们描述了ODTE算法，该算法用于捕获时空数据，并在汇聚节点上进行数据跟踪与数据估计。ODTE算法从以下两个方面进行说明：

3.1 空间-时间数据相关性

在无线传感器网络中，汇聚节点用于提取来自传感器节点的连续数据流。在汇聚节点获取的观测数据通常具有空间相关性。在本小节中，我们描述了如何利用Karjee和 Jamadagni（2011，2012）中考虑的观测数据的空间相关性，来构建ODTE算法的基础。在时间间隔 t，观测数据向量 vt计算得到一个协方差矩阵，其表达式为

$$
E[vtv T t] ≈ UE[αt α T t]U T . (4)
$$

协方差矩阵 E[vt v T t]是一个满秩矩阵，被近似为低秩矩阵用于数据跟踪。该协方差是一个 m × m矩阵，它捕获了在由 UU T张成的子空间下的观测数据以及一个d × d维的低秩矩阵 α t α T t 。我们希望利用这种近似来捕获时空数据矩阵，因为每个列 v t 在时间间隔 t内在汇聚节点处被跟踪。根据方程(4)，我们计算在离散时间函数t下传感器节点i和j之间的数据相关矩阵corr{vi , v j}(t)。因此，数据相关矩阵由下式给出

$$
corr{vi , v j }(t)= \frac{cov{vi , v j }(t)}{\sqrt{var(vi)}\sqrt{ var(v j )}}; i, j ∈ m; ∀ t,(5)
$$

其中 $\sqrt{var(vi)}$ = σvi 和 $\sqrt{var(vj)}$ = σvj 是在时间间隔 t 内从传感器节点收集的数据样本的标准差。根据公式（4）和（5），我们定义在时间间隔 t 下具有时空相关性的数据协方差矩阵为

$$
E[vtv T t] ≈ cov{vi, vj}(t)= σviσvj corr{vi, vj}(t). (6)
$$

我们采用Olivera等人（1997）的相关模型 K(.)，该模型由Vuran等人（2004）给出，以获得相关矩阵（6）。

$$
corr{vi, vj}(t) ≈ K(qi,j)(t) (7)
$$

在公式（7）中，corr{vi, vj}(t) 是一个相关矩阵，用于捕捉在离散时间间隔 t的函数下，分别位于 vi和 vj位置的传感器节点 i和j之间提取的数据的时空特征。因此，该相关矩阵可近似为相关模型 K(qi,j)(t)，其中qi,j=∥ vi − vj ∥是分别位于 vi和 vj位置的传感器节点 i和 j之间的欧几里得距离，并考虑离散时间间隔 t的影响因子。 K(qi,j)(t) 是一个随着qi,j=∥ vi − vj ∥(t) 时间推移而单调递减的函数，在 q= 0处极限值为1，在q= ∞处极限值为0，如Vuran等人（2004）所述。因此，它是一个时空依赖函数，用于在时间间隔 t内从网络中的传感器节点间提取数据。由公式 （6）和（7）可得

$$
| σ^{-2}_{vi, j} E[vtv T t] − K(qi,j) |≤ ψ; ∀ t (8)
$$

使得由公式（4）和公式（7）导出的两个近似之间的差值在时间间隔t内满足小于一个小的正值 ψ的边界条件。传感器节点 i和 j使用近似 E[vtvt]收集它们之间的时空数据方差σ2 v i, j ，并计算传感器节点 i和 j之间的欧几里 得距离，以使用近似 K(qi,j)在网络内形成数据相关矩阵。这意味着，我们用在时间实例 t的 i和 j项对 E[vtv T t]中的 i和 j项进行近似。这两个近似的取值应使其之间的差值小于范围 ψ，且仅当公式（8）满足时，传感器节点 i和 j在 K(qi,j)中的数据方差 σ2 v i, j才具有时空相关性。此外，公式（7）可以用幂指数模型Olivera等人（1997） 和Berger等人（2001）表示为

$$
P= K(qi, j)( t)=
\begin{pmatrix}
e^{-(q_{1,1}/\theta)} & \cdots & e^{-(q_{1,m}/\theta)} \
e^{-(q_{2,1}/\theta)} & \cdots & e^{-(q_{2,m}/\theta)} \
\vdots & \ddots & \vdots \
e^{-(q_{m,1}/\theta)} & \cdots & e^{-(q_{m,m}/\theta)}
\end{pmatrix}, (9)
$$

θ是范围参数，用于控制传感器节点在时间间隔 t内的数据相关性。由于感知节点之间相距较远，根据 Vuran等人（2004）在网络中的研究，它们之间的数据相关性随时间逐渐降低。

在我们的模型中，我们分别从方程(4)和(7)得到两个近似。第一个近似是

由于 E[αtαtT]的低秩矩阵的偏差。类似地，我们得到另一个近似，该近似源于 K，用于捕捉网络中传感器节点之间的相关数据。这两个近似共同导致了式(1)中的系统噪声 γt的产生。因此， γt是由协方差矩阵 E[vtvtT]中低秩矩阵和 K矩阵的近似偏差共同产生的。结合这两个近似，我们得到一个小型矩阵 d × d，其表示为

$$
E[αtα T (10)
$$

此外，可以使用方程(10)来近似方程(4)

$$
E[vtv T (11)
$$

利用方程(6)、(9)和(11)，我们表示一个数据协方差矩阵，使得 RUU= E[vtv T t] ≈ σ2 vi,j K(qi,j)。它捕捉了传感器节点之间的数据方差 σ2 vi,j ，并且还依赖于 K(qi,j)(t)，其中 q是网络中在时间间隔 t位于 vi和 vj位置的传感器节点之间的欧几里得距离。我们用 RUU表示

$$
RUU=
\begin{pmatrix}
σ_{v1} σ_{v1} e^{-(q_{1,1}/\theta)} & \cdots & σ_{v1} σ_{vm} e^{-(q_{1,m}/\theta)} \
σ_{v2} σ_{v1} e^{-(q_{2,1}/\theta)} & \cdots & σ_{v2} σ_{vm} e^{-(q_{2,m}/\theta)} \
\vdots & \ddots & \vdots \
σ_{vm} σ_{v1} e^{-(q_{m,1}/\theta)} & \cdots & σ_{vm} σ_{vm} e^{-(q_{m,m}/\theta)}
\end{pmatrix}
(12)
$$

我们希望测量某个环境中的物理现象（例如温度）。我们将物理现象视为一个参考向量，将在网络中对其进行感知和测量。假设 y（公式(2)）为待被传感器节点在时间间隔 t内感知的参考向量。因此，传感器节点从物理现象中捕获数据相关性，并将其表示为 RUy向量

$$
RUy = E[Uty]= σ_y
\begin{pmatrix}
σ_{v1} e^{-(q_{y,1}/\theta)} \
σ_{v2} e^{-(q_{y,2}/\theta)} \
\vdots \
σ_{vm} e^{-(q_{y,m}/\theta)}
\end{pmatrix} (13)
$$

3.2 数据跟踪与估计机制

考虑到初始假设(1)，并受Balzano等人（2010）提出的 GROUSE启发，我们通过在每个时间间隔 t={1, 2,…, T}观测到的向量序列v t来描述网络中的在线数据跟踪，其中v t ∈ S(t)。 S(t) ∈ Gr(m, d)用m × d正交矩阵 U t表示。利用公式(2)，我们从由 U t张成的子空间 S(t)中评估 y，以跟踪观测向量v t 。使用权重向量 y，我们计算一个预测向量作为

$$
h= U_t y . (14)
$$

我们在时间间隔t评估残差加权向量

$$
w=(v_t −h) (15)
$$

使用Balzano等人（2010）提出的GROUSE，通过步长 ηt更新子空间以用于 S(t) = S0，适用于所有t，其中 limk→∞ ηt= 0和∑∞ k=1 ηt= ∞，并取 ηt α 1 t以满足条件。最后，更新由以下给出的子空间

$$
U_{t+1}= U_t+\left((\cos(\xi\eta_t)- 1) \frac{h}{|h|}+ \sin(\xi\eta_t) \frac{w}{|w|}\right) \frac{y^T}{| y |}, (16)
$$

其中 ξ=∥ w ∥∥h ∥。方程(16)的详细说明在Balzano等人（2010）中有广泛阐述。一旦使用GROUSE完成在线数据跟踪，我们便关注在时间点 t于网络中进行的数据估计。我们根据公式(12)计算奇异值分解 RUU= UΛUT。对角矩阵 Λ的对角线元素 λi= {λmax,…, λmin}称为特征值。选择合适的特征值对于ODTE算法的平稳收敛至关重要。受自适应滤波概念 （Sayed, 2008）的启发，我们考虑适当正的步长参数 µ，其中 µ> 0定义为

$$
0< µ ≤ ρ ∗(2/λ_i), (17)
$$

其中 ρ是介于 0< ρ ≤ 1之间的正数。在最速下降算法 （Sayed, 2008；Lopes 等, 2007）中使用公式(12)、 (13)、(15)和(17)，可得到在时间t+1处相对于初始残差向量w的新更新残差向量，该向量在时间 t给出为

$$
w∗= w+ µ[RUy − RUUw]. (18)
$$

我们的目标是利用对齐（公式(18)）以及由 Ut张成的子空间与观测向量 vt进行数据估计，找到代价函数 J(w∗) (3)。对代价函数 J(w∗)进行归一化，得到失真因子

$$
DF=(1 − \frac{J(w ∗ )}{σ^2}) (19)
$$

失真因子用于计算网络中的数据估计。因此，ODTE算法在网路的汇聚节点处利用DF捕获空间相关数据，并进行在线数据跟踪与数据估计。我们在算法1中总结了ODTE。

算法1 在线数据跟踪与估计（ODTE）

需要：一个 m× d正交矩阵 U0。在网络中跟踪一系列向量 vt。采用步长 ηt。
返回：子空间 Ut在时间 t的失真因子（D.F）。

1: For t=1,2,....... T do
2: 权重向量： y= arg minα ||(Utα − vt)|| 2
3: 计算预测向量： h= Uty
4: 计算残差加权向量： w= vt −h
5: 使用GROUSE更新子空间： Ut+1= Ut+((cos(ξηt) − 1) h ‖h‖ + sin(ξηt) w y T ‖y‖ 其中 ξ=‖ w ‖‖ h ‖
6: 更新残差向量： w∗= w+ µ[RUy − RUUw] RUU= E[UtU T t]= σvi σvj e−(qi, j /θ RUy = E[Uty]= σ y σvi e−(qy ,i /θ 其中),) 以及 RUU= UΛU T 的SVD。从 Λ 中取最大特征值(λmax) 得到 µ: 0< µ ≤ ρ ∗(2/λmax)。
7: 代价函数定义为：J(w ∗)=minw ∗ ||vt − UtU T t w ∗||2
8: 归一化代价函数：D.F=(1 − J(w ∗ ) σ2 v)
9: End for

无线传感器网络中基于预测切换机制的数据估计

4 网络中的数据预测机制

在上一节中，我们开发了用于汇聚节点进行数据跟踪与数据估计的ODTE算法。ODTE有助于高效处理数据，并可通过汇聚节点处的近似机制找到数据存储的最优解。这可能有助于提高无线传感器网络中的数据处理速度和实现最优数据存储。在本节中，我们致力于利用Ali 等 (2008a)在无线传感器网络中提出的近似数据来开发预测方法。与上一节讨论的近似方法不同，另一种数据逼近方式是在网络中通过自适应、数据估计和数据预测对数据进行训练。为了更好地理解预测机制，我们假设每个传感器节点和汇聚节点都将数据存储在桶中。桶是就像在缓冲区中存储数据的容器一样。我们将缓冲区视为桶中用于存储数据的一块可用空间。我们在汇聚节点的桶中设定一个预测误差 ES和阈值 TS。类似地，每个节点 i为其对应的传感器节点桶计算一个预测误差Ei及其相应的阈值 Ti，适用于, 2,…m个传感器节点的桶。数据从传感器节点的桶传输到汇点的桶。一旦数据被汇点桶接收，就利用缓冲区中的数据进行 ES ≥ TS训练。如果 ES ≤ TS，汇聚节点进入估计阶段，并向所有传感器节点发送请求以停止数据传输。在此阶段，每个传感器节点的 Ei ≥ Ti，节点继续向汇点桶传输数据。如果 Ei ≤ Ti，传感器节点 i停止向汇点传输数据，并开始为传感器节点预测数据。这意味着，我们希望开发预测机制，使得节点桶中的数据在经过一定时间后不再被传输，从而节省汇点处的数据并减少汇聚节点的数据存储容量需求。

数据逼近是在限定范围内传输最小数据的一种有效方法，该方法由桑蒂尼和罗默（2006）以及Ali 等 (2008a) 提出于汇聚节点处进行数据预测。以下方法在无线传感器网络的通信开销和能量节约方面可能较为高效。通常，为了在汇聚节点获得数据逼近，并受Karjee和 Jamadagni（2013）启发，我们分别构建了C‐DPS和R‐DPS模型。这两个系统首先对数据进行训练（即训练阶段），以良好适应相应数据，随后进入估计阶段，计算输入与感知数据的估计输出之间的误差，并判断其是否在阈值范围内，从而实现对未来感知数据的预测。我们将此阶段称为预测阶段，在此阶段汇聚节点开始预测感知数据，并限制传感器节点停止进一步的数据传输。对于C‐DPS系统，我们在汇聚节点处使用预测误差 ESC和阈值 TSC的表示。类似地，对于每个传感器节点 i，它评估预测误差 EiC和一个固定的阈值 TiC。对于 R‐DPS系统，我们在汇聚节点处使用预测误差 ESR和阈值 TSR。类似地，对于每个传感器节点 i，我们使用预测误差 EiR和一个阈值 TiR。我们接下来讨论预测机制。

4.1 列向数据预测系统

使用在线跟踪机制进行数据估计是网络中提取数据的一项高效任务。在线数据跟踪机制首先对数据进行训练，这种采用数据模式的操作方式即为训练阶段。一旦在汇聚节点接收到的数据完成训练，系统便开始对网络中的数据进行估计和进一步预测。C-DPS的细节大致说明如下：

i 训练阶段 ：在此阶段，汇聚节点存储从传感器节点传输的数据，并跟踪每个时间实例的数据向量序列。它对网络进行数据训练。初始时，汇聚节点利用由 Ut张成的子空间S(t)，并通过在时间间隔 t内的残差加权向量w(公式(15))，根据公式(1)计算出期望的数据向量 gt

$$
gt= UtU T t w+ ςt, (20)
$$

其中 ςt为加性高斯白噪声。汇聚节点使用由 Ut张成的子空间以及更新残差向量 w∗（公式(18)）来更新其预测向量(14)。更新后的预测向量相应地训练数据，以了解网络中的数据模式。它对汇点处数据的统计行为进行总体概括，以更新预测向量。因此，更新后的预测向量由下式给出

$$
h ∗ = UtU T t w ∗ . (21)
$$

一旦在汇聚节点计算出更新后的预测向量，我们便评估预测误差。预测误差定义为输入的期望感知数据与预测向量输出之间的误差。因此，我们在汇聚节点处评估预测误差，其表达式为

$$
E S mB =| gt −h ∗ | . (22)
$$

我们定义一个阈值 T S C ，其中 0< T S C ≤ 1。如果 E S C > T S C ，汇聚节点将对数据进行更长时间间隔的训练，从而使C‐DPS模型在汇聚节点处得到良好适应。这使得汇聚节点能够切换至训练阶段。它会持续适应感知数据，直到每个时刻的预测误差 E S C 低于阈值 T S C 。

ii 估计阶段 ：当预测误差 ES C 低于阈值时，汇聚节点切换到估计阶段，即 ES C ≤ T S C 。在估计阶段，汇聚节点执行以下操作：

汇聚节点通过由 Ut张成的子空间更新期望的数据向量 gt(公式(20))，然后根据公式(18)给出的残差向量 w∗进行更新

$$
g∗ t= UtUT t w ∗+ ςt. (23)
$$

b 汇聚节点存储数据向量， g∗ t和 w∗分别由g∗ t=(ϱ∗ 1, ϱ ∗ m)T和 w∗(ω∗ 1, ω∗ 2,…, ω∗ m)T表示，对应i= 1,2,…, m个传感器节点。汇聚节点将绑定信息值{ϱ∗ i, ω∗ i}发送到每个传感器网络中的节点i。每个传感器节点i接收绑定信息值{ϱ∗ i, ω∗ i}，并利用该信息进行数据预测的进一步更新。在这种情况下，汇聚节点进入估计阶段。

在每个传感器节点上， CDPS模型的工作方式如下：一旦每个传感器节点接收到绑定信息{ϱ∗ i, ω∗ i}，它就开始计算初始预测值

$$
~= viϱ ∗ i, (24)
$$

其中 vi是 i传感器节点的感知数据。初始预测值~结合感知数据 vi和 ϱ∗ i，用于使每个节点 i在每一时刻提取数据统计信息。我们通过以下方式计算每个传感器节点的残差加权值

$$
fi= ϱ∗ i −~i. (25)
$$

使用自适应LMS滤波器，我们更新残差加权向量 ω∗ i为

$$
ω∗∗ i= ω∗ i+ µvifi, (26)
$$

其中 µ由公式(17)推导得出。我们可以根据每个传感器节点的初始预测值~（公式24）进行更新

$$
~∗ i = viω ∗∗ i . (27)
$$

预测值~∗ i概述了每个传感器节点上数据的统计模式。最后，我们在每个传感器节点上评估预测误差值

$$
Ei C =| ϱ ∗ i −~∗ i | . (28)
$$

我们在每个 i传感器节点上定义阈值 T i C ，其中 0< T i C ≤ 1。如果 E i C ≥ T i C ，每个节点 i传输数据以适配C‐DPS模型。

预测阶段 ：如果对于每个传感器节点 E i C ≤ T i C i，节点将停止向汇聚节点传输数据。在这种情况下，汇聚节点切换到预测阶段，并提取预测的近似数据以供汇聚节点进一步处理。此外，如果期望数据 ϱ ∗ i 与预测值~∗ i 之间的差值超过阈值 T i C ，传感器节点将重新开始向汇聚节点传输数据。此时，汇聚节点进入训练阶段。汇聚节点利用新到达的数据进行自适应调整，整个系统在预测阶段和训练阶段之间运行。整个过程相应地重复，以控制C‐DPS模型。

我们在算法2中总结了C‐DPS系统。

算法2 按列数据预测系统

需要： 一个 m× d正交矩阵 Ut，向量序列 vt和ODTE算法。
返回：汇聚节点的数据预测。

汇聚节点操作：

1: for t=1,2,....... T do
2: Desired data vector: gt= UtU T t w+ ςt
3: Prediction vector: h∗= UtU T t w ∗
4: Prediction error: ESC=| gt −h∗ |
5: Define threshold value: TSC, where 0< TSC ≤ 1
6: if ESC > TSC then → Switched to Training phase.
7: else ESC ≤ TSC → Update 2 by g∗ t= UtU T t w ∗+ ςt → Stored data vectors g∗ t=(̺∗ 1, ̺∗ 2,…, ̺∗ m)T and w∗=(ω∗ 1,ω∗ 2,…,ω∗ m)T for i= 1, 2,.., m → Sink node transmits{̺∗ i, ω∗ i} to each i nodes → Switched to Estimation phase.
8: end if

每个节点的操作：

1: Each node i receives{̺∗ ,ω∗ i}.
2: Predicted value:~i= vi̺ ∗ i
3: Residual weighted value: fi= ̺∗ −~i
4: Update weighted value: ω∗∗ = ω∗ i + µvifi;
5: Update 2 by~ ∗ i ← viω ∗∗ i ;
6: Predictive error: Ei C =| ̺∗ i −~ ∗ i |
7: Defining threshold value: Ti C where 0< Ti C ≤ 1
8: if Ei C > Ti C then → adapts data at each sensor node.
9: else Ei C ≤ T i C → nodes stop transmitting data. → sink switches to Prediction Phase.
10: end if
11: end for

4.2 逐行数据预测系统

汇聚节点以固定的时间间隔从每个传感器节点接收 n块数据的行。我们假设汇聚节点接收并存储来自网络中每个传感器节点 i的样本向量[v 1 i , v2 i ,…, vn i] ∈ R n的 n块数据。下面我们讨论R‐DPS模型在邻近节点和汇聚节点上执行的操作：

步骤一（邻近节点） ：传感器节点i采集观测数据，并在固定时间间隔内将由Karjee和Jamadagni（2013）提出的连续 n个样本数据块 v=[v 1 i , v 2 i , v 3 i ,… v n i]传输至汇聚节点。我们假设每个邻近节点在时间间隔 t向汇聚节点传输的数据长度为 v，大小为 l字节

$$
l ( v i ) =[l( v 1 i ) , l( v 2 i ) , l( v 3 i ) ,… l ( v n i )] , (29)
$$

其中 l以要传输的比特消息表示。)的大小可能根据用户需求在向汇聚节点传输数据时有所不同。

备注 ： 在R‐DPS模型中，我们考虑对传感器节点 i传输的单比特数据l ( v i ) =l ( v i )进行处理传输一个数据块流 l 字节。这使得在汇聚节点处的数据跟踪机制比 Karjee和Jamadagni（2013）提出的 STDP模型 更快。为了及时高效地处理和跟踪数据， R‐DPS模型 采用处理单比特数据（即 lv= lv）来执行预测模型。通常，在执行 R‐DPS模型 时，我们在网络中的时间实例 t仅处理单比特数据。为了更好地理解下面给出的 R‐DPS模型，我们考虑 lv 为每个传感器节点传输到汇聚节点进行处理的一个包含 n 行、每行一个字节的数据块。

每个相邻的传感器节点i计算一个标量测量，该测量在 Karjee和Jamadagni（2013）中被考虑，用于传输l(vi)并将其处理到汇聚节点

$$
l(ui)= l(vi)z0+ ςi, (30)
$$

其中 z0是（n × 1）一个权重向量， ςt是一个不相关噪声信号，且 z0=[1, 1, 1,…, 1]T/√n洛佩斯等人（2007）。邻近节点i通过加性高斯白噪声（AWGN）信道将l(vi） 字节的观测数据传递给汇聚节点，该信道在 Li 等人（2006）和戈布利克等人（1965）中被考虑。

步骤二（汇聚节点） ：它从邻近传感器节点在 lv数据矩阵中传输的已观测 l字节数据消息以及Karjee和Jamadagni（2013）给出的对应标量测量中提取信息，表示为 lu行向量

$$
Lv=[l(v1), l(v2), l(v3),… l(vm)] T (M × N) (31)
$$

$$
lu=[l(u1), l(u2), l(u3),… l(um)] T (M × 1). (32)
$$

使用自适应最速下降法赛义德（2008）和洛佩斯等人 （2007），汇聚节点计算全局统计信息{RV V, RUV}，如Karjee和Jamadagni（2013）中所考虑的，其中 RV V= E[LT v Lv]和 RUV=E[LT v lu]。全局统计信息用于检测网络中的数据模式。它也可以用近似形式表示，使得 RV V是一个 n × n矩阵，由 Lv数据矩阵、其转置以及 UUT数据相关协方差矩阵组成。类似地， RUV是 一个 n × 1向量，包含 lu、其转置数据以及 UUT。该全局统计信息捕获网络中的空间相关数据以及由 U张成的子空间。我们对其进行如下近似

$$
R V V ≈ E[L T v UU T L v] and R UV ≈ E[L T v UU T l u].(33)
$$

采用 Karjee和Jamadagni（2013）提出的自适应滤波方法（Lopes 等, 2007）以及由公式(17)推导出的 µ，在汇聚节点处估计的全局加权向量为

$$
z_{Glob_k} = z_{Glob_{k-1}} + \mu \sum_{i=1}^{m} (RUV_k - RV V z_{k-1}) (34)
$$

经过 k次迭代。全局加权向量捕获了 R V V 和 R UV 内部的数据模式。根据与迭代相关的步长（Sayed, 2008），我们可以将 µ写为一个与迭代相关的正步长 µ(k) 以及最小均方（LMS）的公式 （34）可以重写为

$$
z_{Glob(LMS) k} = z {Glob_{k-1}} + \mu(k) \sum_{i=1}^{m} (RUV_k - RV V z_{k-1}). (35)
$$

使用归一化最小均方（NLMS），我们考虑一个向量 RUV 和一个协方差矩阵 RV V，以通过给定的代价函数获得最优加权向量 z

$$
J(z)= min_z ||RUV − RV V z||^2. (36)
$$

在公式(35)上实施正则化牛顿递推（Sayed, 2008），我们对NLMS的全局加权向量进行近似

$$
z_{Glob(NLMS) k} = z {Glob_{k-1}} + \mu(k)(\epsilon(k)I+ RV V)^{-1} \times \sum_{i=1}^{m} (RUV_k - RV V z_{k-1}), (37)
$$

其中 ϵ(k)是一个正标量。我们假设步长 µ(k) =µ且 ϵ(k) = ϵ。因此， zGlob(NLMS) k 被表示为

$$
z_{Glob(NLMS) k} = z {Glob_{k-1}} + \mu(\epsilon I+ RV V)^{-1} \times \sum_{i=1}^{m} (RUV_k - RV V z_{k-1}). (38)
$$

根据瞬时近似（Sayed, 2008），我们将(ϵI+ RV V)替换为(ϵI+ lT v i lvi )，并将(RUV, k − RV V zk−1 l (ui l T (vi − l (vi z Glob k−1 )替换为)(> ))。全局统计信息变为

$$
RV V,i= lT (vi) l(vi) and RUV,i= lT (vi) l(ui) . (39)
$$

我们需要在每次迭代中通过应用赛义德（2008）的矩阵逆公式对 ϵI+ RV V进行逆运算，且在汇聚节点计算出的全局加权向量 z Glob(NLMS) k 为

$$
z_{Glob(NLMS) k} = z {Glob_{k-1}} + \mu p \sum_{i=1}^{m} l T (vi) (l(ui) − l (vi) z_{Glob_{k-1}}), (40)
$$

其中p= ϵ+ ∥l(vi )∥ 2。其余工作原理与Karjee和 Jamadagni（2013）提出的STDP模型类似。为保持工作的连续性，我们将其总结如下：在汇聚节点处，计算预测向量 l sink =L v z Glob ( NLMS ) k 以及预测误差。

$$
E S R =| l u − l sink | . (41)
$$

预测误差 E S R 控制网络中的数据传输。在汇聚节点处定义了一个阈值 T S R ，其中 0< T SR ≤ 1，以实现两个目的：

• 如果 ESR ≥ TSR，邻近节点将像往常一样向汇聚节点传输数据。在这种情况下，汇点接收到的数据将被相应采用。
• 如果 ESR ≤ TSR，汇聚节点将 zGlob(NLMS) k发送到每个传感器节点。这类似于汇点向邻近传感器节点发出的请求，以停止数据传输，如Karjee和Jamadagni（2013）中所述。

第三步 (邻近节点) ：当每个邻近的传感器节点接收到 zGlob(NLMS) k 后，使用 zGlob(NLMS) k 计算其自身的权重向量和预测误差。每个节点评估一个期望值

$$
l(u_{new_i})= l(vi)z_{Glob(NLMS)_k} + ςi. (42)
$$

每个相邻传感器节点计算出的新权重向量由

$$
z_{new_{i,k}}= z_{i,k−1}+ \mu \sum_{i=1}^{m} lT(vi)( l(u_{new_i}) − l(vi)z_{i,k−1}). (43)
$$

每个传感器节点计算其预测滤波器值为 lnew i=l(vi) znew i k,。在每个传感器节点i处评估的预测误差由以下公式给出

$$
EiR =| l(u_{new_i}) − l_{new_i} | . (44)
$$

定义一个阈值 TiR ，其中 0< TiR ≤ 1 用于满足以下条件：

• 如果 Ei R ≥ Ti R ， l(vi)将从每个传感器节点 i传输到汇聚节点。
• 如果 Ei R ≤ Ti R ，则传感器节点 i停止传输 l(vi)并将其 z新i，k值传送给汇聚节点。这类似于邻近传感器节点向汇聚节点响应，表示它们不再希望向汇聚节点传输数据，直到 Ei R ≥ Ti R ，然后该过程从步骤‐I重新开始。由于邻近节点不再传输数据，汇聚节点开始预测数据，从而可能减少网络的传输开销。

我们在算法3中总结了R‐DPS模型。

4.2.1 能量降低模型

在 Heinzelman 等人 (2002) 中考虑的经典能量模型被应用于一种数据预测模型，即 R‐DPS 模型，以获得无线网络中的能量性能。每个传感器节点 i提取并传输 n个数据样本到汇聚节点。汇点在固定时间间隔内收集 v=[v 1 i , v 2 i , v 3 i ,… v n i]个数据样本向量，其 l字节的数据长度为 l( v i ) =[l( v 1 i ) , l( v 2 i ) , l( v 3 i ) … l( v n i )] ,，其中l表示一条消息的一位。在 R‐DPS 模型中，我们考虑在固定时间间隔向汇聚节点传输单比特数据 l( v i ) = l( v 1 i )。根据 Heinzelman 等人 (2002) 提出的能耗模型，网络中消耗的能量如下

$$
E_{Total_{Sink}} = E_{Sink} + \sum_{i=1}^{m-1} E_{NonSink} , (45)
$$

其中， ESink 是汇聚节点消耗的能量， ENonSink 是邻近节点的能耗， m 是网络中的传感器节点数量。采用 Heinzelman 等人 (2002) 提出的无线电硬件耗散模型，该模型中发射天线消耗能量以运行无线电电子设备。我们考虑自由空间信道模型和多径衰落信道模型，以根据 Heinzelman 等人 (2002) 中给出的发射天线与接收天线之间的距离进行调整。定义了一个阈值 ξ ，如果距离小于 ξ，则使用自由空间信道模型，否则使用多径衰落信道模型。在网络中传输数据所消耗的能量表示为

$$
ETX= l(v1i)EElec+ l(v1i)ϵfsd^2 \quad \text{for} \quad d< \xi \quad (46)
$$

$$
ETX= l(v1i)EElec+ l(v1i)ϵmpd^4 \quad \text{for} \quad d ≥ \xi. (47)
$$

算法3 逐行数据预测系统

需要：来自传感器节点到汇聚节点传输的单比特数据长度 l(vi)= l 及其对应的标量值 l(ui)。
返回：汇聚节点处的数据预测。

汇聚节点操作：

1: 计算全局统计信息{RV V, RUV}，其中 RV V= E[L T v Lv]和 RUV=E[L T v lu]来自Lv=[l(v1) l(v2) l(v3) · · · · · · · · · l(vm)]T以及lu=[l(u1) l(u2) l(u3) · · · · · · · · · l(um)]T。
2: 全局加权向量： z Glob(NLMS) k = z Glob k−1 +µ(ǫI+ RV V)−1∑ m i=1( RUV, k − RV Vzk−1)。
3: 将(ǫI+ RV V)替换为(ǫI+ l T v i lv i) ，并将(RUV, k − R V V z k−1 l(ui l T (vi − l (vi z Glob k−1 R V V i=)替换为)( ) ) )，其中,l T (vi) l (vi)和 R UV,i= l T (vi) l (ui)。
4: 修正的全局权重向量： z Glob(NLMS) k = z Glob k−1 + µ ǫ+‖l (v i ) ‖ 2 ∑ m i=1 l T (vi)({ R V V , RUV}) −l (vi) z Glob k−1)
5: 预测向量： l sink = L v z Glob(NLMS) k
6: 预测误差：E S R =(lu − l sink)
7: 定义阈值：(TSR )，其中 0< T SR ≤ 1
8: 如果 E S R ≥ T S R ，则→切换到训练阶段。
9: 否则 E S R ≤ T S R ,→汇聚节点将 z Glob(NLMS) k 传递给每个节点→切换到估计阶段。
10: 结束如果

每个节点的操作：

1: 期望值：l (u new i ) = l (v i) z Glob(NLMS) k + ς i
2: 计算权重向量：z new i,k = z i,k − 1 +µ∑ m i =1 l T (v i )(l(u new i ) − l (v i) z i,k − 1)
3: 预测滤波器：l new i = l (v i )z new i k ,。
4: 预测误差：E i R =| l (u new i ) − l new i)|
5: 定义阈值：T i R 其中 0< T i R ≤ 1
6: 如果 Ei R ≥ T i R 则→ l (v i ) 从每个传感器节点 i传输到汇点。
7: 否则 Ei R ≤ T i R ,→节点停止传输数据→汇点切换到预测阶段。
8: 结束 if

汇聚节点从传感器节点接收数据所消耗的能量表示为 ERX= l(v1i)EElec，其中 EElec 是电子能耗，表示信号传播。Heinzelman 等人 (2002) 提出的能量模型中使用的参数如下： EElec=50nJ/bit, ϵfs= 10pJ/bit/m2, ϵmp= 0.0013pJ/bit/m4 以及在汇点处的数据聚合，表示为 EAgg= 5nJ/bit/信号。我们考虑汇聚节点与传感器节点之间的距离 d= √ ϵfs ϵmp ， 如Heinzelman等人(2002)中所给出的。网络中传感器节点到汇聚节点之间采用自由空间模型。网络中每个传感器（非汇聚节点）的能耗表示为

$$
ENonSink= ETX= l(v1i)EElec+ l(v1i)ϵfsd^2 \quad \text{toSink}. (48)
$$

邻近节点位于距汇聚节点坐标(a, φ)范围内，积分如下

$$
ENonSink= ETX= l(v1i)EElec + l(v1i)ϵfs \int_{0}^{2\pi} \int_{a}^{r} 2\omega a da d\phi, (49)
$$

其中 r定义了每个传感器节点的空间数据相关范围，以及ω= m πr2。

$$
ENonSink= ETX= l(v 1 i)EElec+ l(v 1 i)ϵfs \frac{mr^2}{2} (50)
$$

邻近传感器节点的数量 m以及每个传感器节点的空间数据相关范围的半径在无线网络场景中是变化的。汇聚节点的能耗通过接收来自邻近传感器节点的数据、数据聚合以及从汇聚节点（无电池驱动）向中央服务器传输数据来衡量。当汇聚节点距离中央服务器（CS）较远时，采用多径信道。汇聚节点消耗的能量由以下公式给出

$$
ESink= ETX+ EAgg + ETx (51)
$$

$$
ESink= l (v 1 i )[mEElec+ mEAgg ++ϵmp d^4_{toCS}]. (52)
$$

考虑到汇聚节点的能耗 ESink和邻近节点的能耗 ENonSink ，网络中由汇点测量的总能耗为ET otalSink。

4.3 DPS模型的应用

我们描述了DPS模型的实际实现，这可能有助于解决工程应用问题。

• 内存管理 ：我们考虑一种客户端‐服务器系统，其中客户端系统始终用于向服务器系统传输数据。服务器分配内存以存储来自客户端的数据。由于客户端持续向服务器传输数据，服务器的内存需要为网络存储海量数据。因此，经过一定时间后，服务器将无法在其内存中继续存储如此海量的数据，从而导致数据溢出网络。在这种情况下，DPS模型可以利用预测机制在服务器中分配内存来存储数据。在这种情况下，服务器中分配的内存会为客户端预测数据，客户端无需始终向服务器传输数据，从而提高服务器的内存管理效率。

• TCP/IP 模型中的拥塞控制 ：当网络无法有效控制网络中的数据流量（如在互联网应用中）时，就会发生拥塞。在通信网络中，由于发送节点总是向接收节点传输数据，网络中的数据流量通常巨大，从而导致传输层出现拥塞。为避免这种情况，DPS模型可帮助发送节点在一定限制内向接收节点传输数据包。同时，接收节点开始对发送节点的数据进行预测，从而利用DPS模型控制网络中的网络流量。

5 仿真和验证

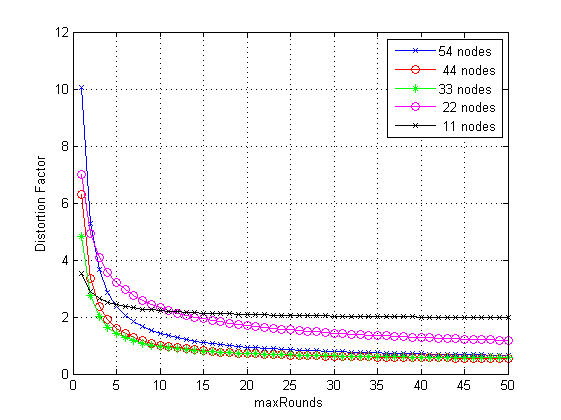
在本节中，我们通过考虑来自部署在英特尔伯克利研究实验室的54个Mica2Dot传感器节点的传感器数据（如英特尔实验室数据中所述， http://db.csail.mit.edu/labdata/labdata.html）来验证 ODTE算法，并在网络中设置一个汇聚节点。Mica2Dot传感器在2004年2月28日至4月5日期间每31秒采集一次湿度、温度、光照和电压值。在我们的实验中，选择2004年2月28日的温度数据，每个传感器节点向汇聚节点传输1000次传感器观测值。我们将d= 7作为网络底层子空间的秩。我们的目标是找到一种在不丢失信息的情况下，控制网络中传感器节点向汇聚节点的数据传输次数的失真因子（DF）。我们将数据传输次数视为称为最大轮数（maxRounds）的轮数。maxRounds定义为每个传感器节点在单位时间内向汇聚节点传输的数据次数。maxRounds用于控制在向汇聚节点传输时的数据流量以及数据的空间相关性。通过寻找传感器节点的maxRounds以获得期望的DF，从而实现可靠数据传输。确定合适的 maxRounds以实现期望的DF，是降低无线传感器网络（ WSNs）中数据传输开销的一项挑战性任务。在ODTE算法中，DF是根据maxRounds对 v t进行估计，以执行在线数据跟踪并将其传输至汇聚节点。在图3中，我们分别随机选取11、22、33、44、54个传感器节点，并计算其在maxRounds= 50下的DF。我们假设在每个传感器节点向汇聚节点传输1000次传感器观测值的过程中，有0.01%的数据丢失。我们在仿真中考虑参数： η t = 0.1、 θ= 70和 ρ= 0.1。从公式（19）和图 3可以看出，随着maxRounds的增加，汇聚节点计算出的不同传感器节点的DF逐渐减小。当达到某一特定的 maxRounds后，不同传感器节点的DF趋于饱和水平，无法进一步降低。这表明向汇聚节点传输更多的数据对改善DF并无额外优势。由于观测数据具有空间相关性，传输最小数据量已足够，无需向汇聚节点传输大量数据。此外，图3显示，考虑54、44和33个传感器节点时产生的失真因子最小，而22和11个传感器节点的失真因子最大。原因是，更多的传感器节点数量会增强传感器节点间的数据空间相关性，从而降低失真因子。当传感器节点数量减少时，由于网络中传感器节点之间的数据相关性降低，导致失真因子增加。以下结果在网络中的数据存储和数据跟踪方面表现出较高效率。

在第二次仿真设置中，我们希望通过在汇点处分别使用 C‐DPS和R‐DPS模型自适应地处理采集到的数据，来预测传感器节点的数据。我们从54个传感器节点中选取 11个节点，向汇点传输1000组观测数据。我们考虑将以下参数用于预测模型： ηt= 0.1、ρ= 0.1、 ϵ= 1、 ς= 10−3、 θ= 70、最大轮数（maxRounds）= 50、d= 7和 TSC = TSR = 0.5。如C‐DPS系统和R‐DPS系统中所述，如果预测误差大于阈值，则汇点继续接收数据；如果预测误差低于阈值，则汇点切换到估计阶段。同样，在每个传感器节点上，我们分别对C‐DPS和 R‐DPS模型评估预测误差和阈值。我们的目标是设定传感器节点的阈值，使得当预测误差小于阈值时，停止向汇聚节点传输数据（针对C‐DPS和R‐DPS）。在此阶段，汇点开始为整个网络预测数据。

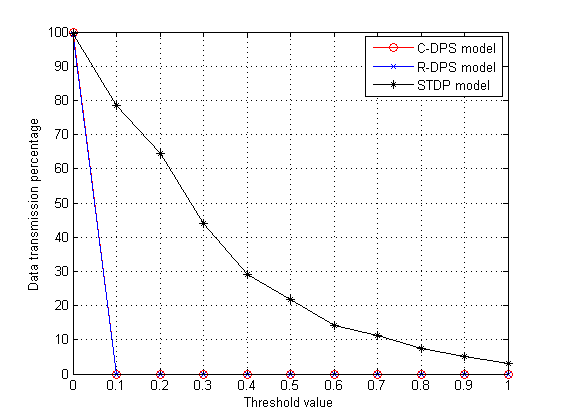
每个传感器节点在经过一定间隔的数据传输后，进入估计模式。传递给汇聚节点的数据数量被表示为数据传输百分比，该百分比是相对于C‐DPS和R‐DPS模型的误差阈值 T i C 和 T i R 进行评估的。在图4中，我们绘制了传感器节点id‐7相对于其阈值 T i C （C‐DPS）和 T i R （R‐DPS）的数据传输百分比，并与STDP模型进行了比较。结果清楚地表明，当达到某个阈值后，传感器节点停止传输数据，从而使汇点开始对该节点的数据进行预测。如图4所示，传感器节点id‐7持续向汇点传输数据，直到其达到C‐DPS的阈值 T i C = 0.1和R‐DPS的阈值 T i R =0.1。一旦数据传输相对于系统的相应阈值，数据传输突然停止，使汇聚节点进入预测模式。当两个系统（C‐DPS和R‐DPS）超过这些阈值后，将不再向汇聚节点传输数据，直到预测误差大于阈值为止。在C‐DPS和R‐DPS模型中，数据传输总是出现剧烈下降；而在STDP模型中，数据传输的下降是平稳且缓慢的，并逐渐超过阈值一。对于节点i d‐7，C‐DPS和R‐DPS在汇聚节点的数据预测在同一阈值处开始。该结果表明，C‐DPS和R‐DPS模型的数据跟踪速度优于STDP模型。C‐DPS和R‐DPS的阈值范围介于0到1之间，因为在C‐DPS中跟踪在线数据时底层子空间不断变化，而在R‐DPS中，网络中的每个传感器节点每次仅跟踪单比特数据。STDP模型的阈值会超过一，因为在该网络中跟踪的是数据块。

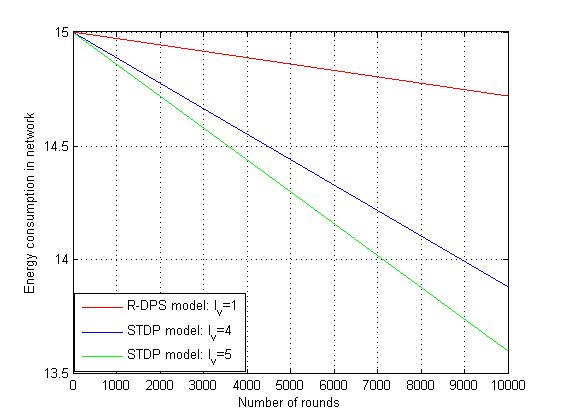
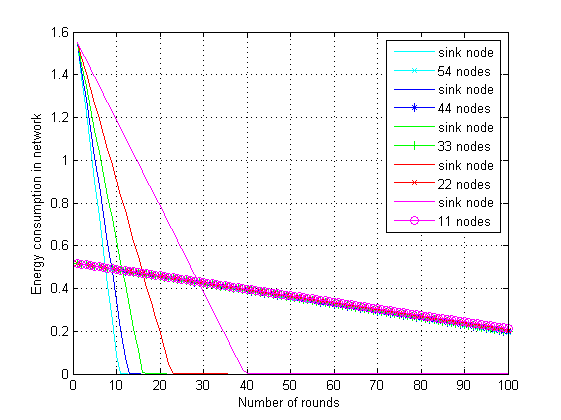
在第三次仿真设置中，我们建立了R‐DPS模型下网络能耗性能，网络规模分别为11、22、33、44和54个传感器节点。在图5中，测量了11、22、33、44和54个传感器节点在汇聚节点处随轮数变化的能耗情况。随着时间推移，网络的生命周期随着能量的耗散，网络规模逐渐减小。结果表明，在考虑54个节点的网络规模时，汇聚节点处的能量耗散更快。同时展示了不同网络规模下汇聚节点的能量耗散随轮数的变化情况。结论表明，如果网络规模（节点数量）较小，则网络中的能耗较低，反之亦然。在最后的仿真设置中，针对54个传感器节点，对Karjee和Jamadagni（2013）提出的STDP模型与所提出的 R‐DPS模型在能量性能方面进行了比较。图6显示， STDP模型比R‐DPS模型能量耗散更快。STDP模型的数据长度 lv