基本二维几何变换
二维平移
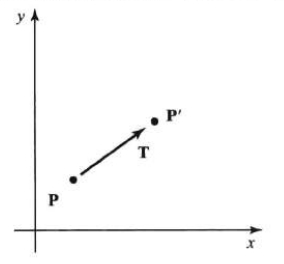
P = [xy]\begin{bmatrix} x \\ y \\ \end{bmatrix}[xy], P’ = [x′y′]\begin{bmatrix} x' \\ y' \\ \end{bmatrix}[x′y′], T = [txty]\begin{bmatrix} t_x \\ t_y \\ \end{bmatrix}[txty]
P′P'P′ = PPP + TTT
二维旋转
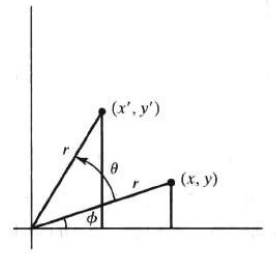
P = [xy]\begin{bmatrix} x \\ y \\ \end{bmatrix}[xy], P’ = [x′y′]\begin{bmatrix} x' \\ y' \\ \end{bmatrix}[x′y′]
xxx = rrr * cos(φ)
yyy = rrr * sin(φ)
P’ 是通过 P 旋转 φ 角的变换而来
x′x'x′ = xxx * cos(φ) - yyy * sin(φ)`
y′y'y′ = xxx * sin(φ) + yyy * cos(φ)`
P′P'P′ = RRR · PPP
R = [cos(φ)−sin(φ)sin(φ)cos(φ)]\begin{bmatrix} cos(φ) & -sin(φ) \\ sin(φ) & cos(φ) \\ \end{bmatrix}[cos(φ)sin(φ)−sin(φ)cos(φ)],
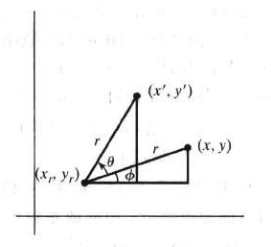
相对旋转点(xrx_rxr, yry_ryr)将点从位置(xxx,yyy)旋转到位置(x′x'x′,y′y'y′)
x′x'x′ = xrx_rxr + (xxx - xrx_rxr) * cos(φ) - (yyy - yry_ryr) * sin(φ)
y′y'y′ = yry_ryr + (xxx - xrx_rxr) * sin(φ) + (yyy - yry_ryr) * cos(φ)
二维缩放

x′x'x′ = xxx * sxs_xsx
y′y'y′ = yyy * sys_ysy
缩放系数 sxs_xsx 在 xxx 方向对对象进行缩放, sys_ysy 在 yyy 方向对对象进行缩放
[x′y′]\begin{bmatrix} x' \\ y' \\ \end{bmatrix}[x′y′] = [sx00sy]\begin{bmatrix} s_x & 0 \\ 0 & s_y \\ \end{bmatrix}[sx00sy] · [xy]\begin{bmatrix} x \\ y \\ \end{bmatrix}[xy]
或
P′P'P′ = SSS · PPP
矩阵表示和齐次坐标
在设计和图形构造的应用中, 通过完成平移、旋转和搜房, 将图形组成部分安排到合适的位置。
每个基本变换(平移、旋转和缩放)都可以表示为普通矩阵形式:
P′P'P′ = M1M_1M1 · PPP + M2M_2M2
P′P'P′, PPP: 列向量
M1M_1M1: 2X2 矩阵
M2M_2M2: 包含平移项的两元素列矩阵
二维平移矩阵
[x′y′1]\begin{bmatrix} x' \\ y' \\ 1 \\ \end{bmatrix}⎣⎡x′y′1⎦⎤ =
[10tx01ty001]\begin{bmatrix} 1 & 0 & t_x \\ 0 & 1 & t_y \\ 0 & 0 & 1 \\ \end{bmatrix}⎣⎡100010txty1⎦⎤ ·
[xy1]\begin{bmatrix} x \\ y \\ 1 \\ \end{bmatrix}⎣⎡xy1⎦⎤
P′P'P′ = TTT(txt_xtx,tyt_yty) · PPP
二维旋转矩阵
[x′y′1]\begin{bmatrix} x' \\ y' \\ 1 \\ \end{bmatrix}⎣⎡x′y′1⎦⎤ =
[cos(θ)−sin(θ)0sin(θ)cos(θ)0001]\begin{bmatrix} cos(θ) & -sin(θ) & 0 \\ sin(θ) & cos(θ) & 0 \\ 0 & 0 & 1 \\ \end{bmatrix}⎣⎡cos(θ)sin(θ)0−sin(θ)cos(θ)0001⎦⎤ ·
[xy1]\begin{bmatrix} x \\ y \\ 1 \\ \end{bmatrix}⎣⎡xy1⎦⎤
P′P'P′ = RRR(θθθ) · PPP
二维缩放矩阵
[x′y′1]\begin{bmatrix} x' \\ y' \\ 1 \\ \end{bmatrix}⎣⎡x′y′1⎦⎤ =
[sx000sy0001]\begin{bmatrix} s_x & 0 & 0 \\ 0 & s_y & 0 \\ 0 & 0 & 1 \\ \end{bmatrix}⎣⎡sx000sy0001⎦⎤ ·
[xy1]\begin{bmatrix} x \\ y \\ 1 \\ \end{bmatrix}⎣⎡xy1⎦⎤
P′P'P′ = RRR(sxs_xsx,sys_ysy) · PPP
其他二维变换
反射
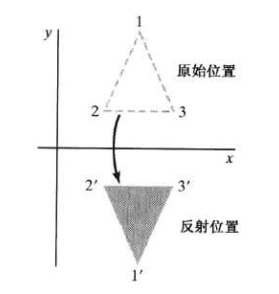
[1000−10001]\begin{bmatrix} 1 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & 1 \\ \end{bmatrix}⎣⎡1000−10001⎦⎤
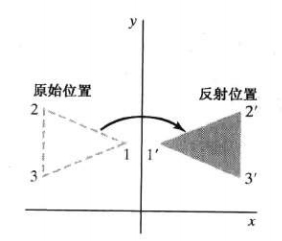
[−100010001]\begin{bmatrix} -1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{bmatrix}⎣⎡−100010001⎦⎤
错切
错切是一种使对象形状发生变化的变换, 经过错切的对象好像是由已经相互滑动的内部夹层组成的。
相对于xxx轴的xxx方向错写由下列变换矩阵产生
[1shx0010001]\begin{bmatrix} 1 & sh_x & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{bmatrix}⎣⎡100shx10001⎦⎤





 本文深入解析二维几何变换,包括平移、旋转、缩放的基本原理及矩阵表示,探讨了齐次坐标的运用,并介绍了反射与错切等其他变换类型。
本文深入解析二维几何变换,包括平移、旋转、缩放的基本原理及矩阵表示,探讨了齐次坐标的运用,并介绍了反射与错切等其他变换类型。
















 535
535

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








