基于分析意图的社区检测算法综述

第12章 基于分析意图的社区检测算法综述

12.1 引言

社区的本质渗透到人类交互的各个方面，系统也不例外。在（社区 2008年）中，将社区的功能定义为“归属结构”。归属的本质至关重要，在任何需要识别群体、参与者或元素的上下文中都至关重要。毫不奇怪，图与网络分析（系统、社会及其他领域）已投入大量资源用于开发能够准确及时进行社区识别的方法。在回顾网络社区检测方法之前，先对网络社区进行功能定义会有所帮助。现实世界网络包含模块化结构，这些结构在上下文中定义了其拓扑或连接性。这些结构通常被定义为节点和边的子集，常常为整个网络的功能提供宝贵的见解。这些结构有多种名称，例如簇、模块或社区（Network analysis 2014; Multiscale ensemble2012; Community Detection2014）。尽管尚未广泛接受一个正式定义，但对这些结构最常见的描述是：在给定网络中，形成一个与其他顶点相区别的凝聚集的一组顶点或簇（Fortunato 2010）。也就是说，凝聚集（社区）中的顶点出现在与网络中其他顶点不同的上下文中。根据这一社区定义，可以明显看出“社区”所处的情境变得多么重要。因此，分析的上下文（分析意图）将影响网络社区检测的性能以及不同方法之间的后续比较。

有许多算法可用于检测网络中的社区结构。虽然并不全面，但在网络社区的背景下，可以将这些算法大致分为四类：零模型、层次聚类、统计推断和基于团的方法（Jin 等2013；社交网络聚类 2011；寻找网络理论 2014； Evans2010）。相关文献通常关注在基准数据集上评估时哪种算法表现最佳。然而，针对同一数据集在不同分析意图下社区发现算法结果的研究却较少。本文尝试围绕上述四个主题领域整理现有文献中的方法，并比较它们在两类分析意图——基于类别和基于事件——下的优缺点。

本文的其余部分安排如下：首先，我们讨论分析意图及其为何是影响网络社区检测算法性能的重要因素。在此部分，我们将探讨两种分析视角：基于类别和基于事件。接着，我们讨论社区结构算法的四大主要类别，以及它们在基于类别的社区检测和基于事件的社区检测中的优缺点。本节中还包括适用于各个类别的算法示例。所讨论的每种算法都试图解决其传统所属类别的某一弱点。在上述讨论之后，我们对全文进行总结。

12.2 分析意图

当网络中出现威胁或问题时，典型的分析通常会同时关注事件本身和归因。因此，涉及网络中社区检测的分析常常将识别/表征与归因结合起来。此外，通常该分析方法论遵循相同的方向，使得难以区分分析方法在问题事件方面的有效性或涉及的个体/角色。基于事件特征或归因属性来确定“归属”常常会产生重叠。当这种区别未被明确定义时先验，每次在同一个网络上运行新的社区检测算法，都可能获得不同的结果（社区检测算法2009年）。结果的质量是基于某种真实情况来衡量的，这种真实情况来源于对评估数据集的另一项分析，该分析定义了哪些网络顶点和节点应包含在每个社区中（Palla 等人 2005）。这种方法的一个缺陷在于，基准数据集通常仅以一种方式进行社区划分，并且依赖于初始的、通常是上下文相关的或人工的划分方案。实际上，网络中往往存在多种顶点群组（社区），而这些社区取决于进行社区发现的个人或组织所期望的分析目的。正因为如此，某些算法会根据评估的高层目标不同而表现得更好。

为了突出分析意图的重要性，我们考虑两种社区检测目的：基于类别和基于事件。基于类别的社区检测分析的目标是根据功能或基于角色的分类度量来识别相关的顶点。在这种情况下，边的流量或其他属性（超出连接本身）并不重要。唯一的要求是两个相连的顶点以某种方式相关，并且它们位于相同的全局网络定义中（即存在于相关网络中）。尽管基于类别的分析意图必须定义某种逻辑连接，但这些顶点之间可能完全没有任何physical连接。第二种类型的分析意图是基于事件的。基于事件的社区检测的目标是根据观测到的连接或边属性来识别社区。这种关注点不要求任何将两个顶点联系在一起的分类类型。唯一的要求是这两个顶点直接相连，或者通过其邻居之间定义的事件链相连。

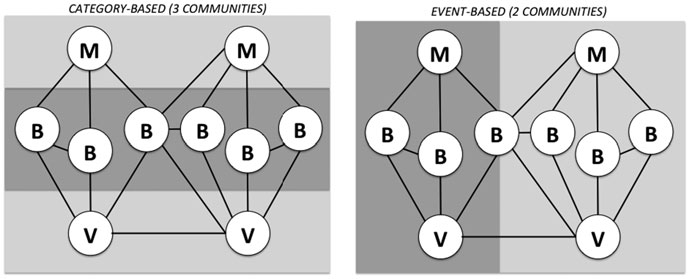
图 12.1说明了在计算机网络上下文中基于类别和基于事件的分析意图的定义。图 12.1展示了一个恶意代理在计算机网络上协同工作的示例网络。这种类型的网络配置通常被称为僵尸网络。僵尸网络在Dietrich等人（2013）中有更详细的描述。尽管僵尸网络可能要复杂得多，但在该图中，我们展示了一个简化的僵尸网络，包含两个僵尸网络控制器，并攻击了两台受害计算机。与任何网络活动一样，存在与这些角色相关的职责和属性。在图中，僵尸网络的主控节点标记为 M1,执行攻击的被劫持节点标记为 B，以及标记为V的受害节点。应用基于类别和基于事件的定义可将网络进行水平和垂直划分。观察图12.1，需要注意的是，在基于类别的社区分析中，节点之间可能不存在定义连通性的边，例如主控节点，尽管它们属于同一个社区。

网络运营商需要出于多种原因分析图 12.1中所示的网络类型。进行分析的两个常见目的是：要么快速关闭网络，要么发现其交易模式以防止未来攻击。当目标是关闭网络时，运营商希望快速识别出控制网络的节点并禁用它们。如图 12.1所示，控制网络的节点之间可能从不进行直接通信，因此仅基于事件发现社区的社区检测算法可能无法快速发现这些控制事件的节点。即使这些算法能够发现此类节点，通常也是通过多个基于事件衍生社区的相关性来实现，而这往往涉及广泛且耗时较长的过程。当目标是发现活动模式以防止未来攻击时，节点的性质或角色就变得不那么重要。在这种情况下，基于连接的基于事件的方法是比基于类别的方法更合理的选择，因为后者并不关注节点之间的直接通信。

12.3 网络社区检测方法

由于网络中社区检测方法试图解决其检测机制中的共性问题，不同方法之间的界限往往变得模糊。这使得很难将这些算法归类为某一种类型。正如布兰廷指出的，社区发现算法由效用函数和搜索策略组成（布兰廷 2011）。效用函数用于确定社区之间划分的质量，而搜索策略则规定了发现网络中的社区的程序。本文根据这两者中的后者对算法进行分类。

最广泛使用的社区检测方法包括：基于层次的、基于空模型的、基于统计推断的和基于团的。基于层次的方法主要关注可以分类的社区。基于零模型的方法主要关注规模相等且社区数量已知的社区。基于统计推断的方法试图通过将生成模型拟合到网络数据来识别社区。基于团的方法则根据在网络中发现的小型完全连通子图来寻找社区。在接下来的子章节中，我们将对每种方法进行更详细的介绍。

12.3.1 基于层次的算法

基于层次的算法从结构或上下文相似性的角度来考虑社区。这些方法中常用的相似性度量包括余弦相似度、汉明距离或杰卡德指数（Chan 等人， 2009年；Jiashun 2012；Dang 和 Viennet 2012）。在基于层次的算法中，根据边的属性计算网络中每对顶点之间的相似性，如果它们足够相似（通常由某个阈值定义），则使用一个nx n相似性矩阵将它们划入同一个社区，其中 n表示顶点的数量。该矩阵通常用树状图表示，并可通过两种方法进行划分： 1. 分裂法：一种自上而下的过程，通过移除连接低相似性顶点的边来迭代地分割顶点组。 2. 凝聚法：一种自下而上的过程，根据高相似性将顶点组进行合并。

12.3.1.1 分裂方法

Girvan 和 Newman 在2002年 提出的催化剂算法使用一种层次化方法，其中网络社区由图拓扑给出。在催化剂算法中，首先根据边中心性绘制网络分析图。边中心性提供了衡量边重要性的指标，依据是在顶点之间可归因的某个选定操作属性或过程。一旦计算出每条边的边中心性，就移除具有最大中心性的边。接着基于剩余的边重新计算中心性，并重复移除具有最高中心性的边。对于使用中心性构建的分析图，随后应用了介数的属性。Girvan 和 Newman 提出了三种介数选项：随机游走介数、电流介数和边介数。

随机游走介数和电流介数的计算对于稀疏图都具有O(n3)的复杂性，而边介数在同一图上的复杂性为O(n2)。此外，研究还表明，在实际图中，边介数的结果也优于其他应用（纽曼和吉尔凡 242 N. C. 帕克斯顿等人 2004）。边介数是指所有顶点对之间的最短路径中经过该边的数量，它是弗里曼在1977年提出的节点介数概念的扩展。社区间边具有较大的边介数值，因为连接不同社区顶点的许多最短路径都会经过这些边。如果存在两条或更多具有相同端点并通过某条边的测地路径，则每条路径对该边介数的贡献必须除以这些路径的重数，因为假设信号/信息沿每条测地路径均等地传播。

利用基于广度优先搜索的技术，可以在时间复杂度为O(mn) 或稀疏图上为 O(n2) 的时间内计算出图中所有边的介数，其中m × n（Yoo 等人，2005）。

在 2004年，纽曼和吉尔凡改进了他们最初的算法，以解决第一版存在的极端可扩展性问题。在最初版本中，作者没有使用效用函数来判断哪些划分更优，因此该算法仅适用于最多包含10000个顶点的网络。即便如此，该算法的运行速度也非常慢（Hierarchical Block Structures2014）。新算法引入了模块度作为质量度量，自那时起这一方法被广泛使用（Nascimento2013）。

2003年，泰勒等人（Tyler 2013）提出了一种对吉尔凡‐纽曼算法的改进方法，以提高计算速度。最初，计算介数的算法必须从一个被认为是中心的顶点开始，计算从该顶点出发的所有路径对介数的贡献；然后对所有顶点重复此过程。在这项工作中，泰勒等人还提出仅从少量随机选择的中心顶点计算边介数的贡献。数值测试表明，对于每个连通子图，选取的中心数量只需随组件顶点数的对数增长即可。对于给定的中心选择，该算法的执行方式与Girvan 和 Newman的算法相同。停止准则不需要划分的模块度，而是依赖于社区的特定定义。根据该定义，一个具有n0个顶点的连通子图，如果其任意一条边的边介数不超过n0−1，则被视为一个社区。实际上，如果该子图由两条部分通过单一边连接而成，则该边的介数值将大于或等于n0−1，只有当其中一部分仅包含一个顶点时等式才成立。因此，对边介数的条件将排除此类情况，尽管其他类型的聚类结构仍可能与此条件兼容。通过这种方式，在泰勒等人的方法中，边被不断移除，直到划分的所有连通分量都成为上述意义上的社区。对边介数的蒙特卡洛采样必然引入统计误差。因此，对于不同选择的中心顶点集合，划分结果通常会有所不同。然而，作者表明，通过多次重复计算，该方法在基因共现网络上取得了良好的结果，并显著节省了计算机时间。该技术还被应用于通过电子邮件通信的人群网络。在实际例子中，只有位于社区边界上的顶点可能无法明确分类，有时被分配到一个组，有时被分配到另一个组。这

这实际上是该方法的一个优点，因为它能够识别社区之间的重叠，以及重叠顶点在其所属簇中的成员度。Girvan 和 Newman 的算法是确定性的，无法做到这一点。

在 2007年 Sales‐Pardo 等人 创建了一种使用该方法的算法。他们基于初始相似性比较构建了一个相似性矩阵。他们将该度量称为顶点亲和性，并使用模块度作为其效用，以发现所识别社区的质量。该算法背后的思想是： 两个顶点之间的亲和性是指它们在对应于模块度局部最优的划分中共同存在于同一社区的频率。每个社区由一组顶点组成，若向该组内再加入一个顶点无法使社区增大（包括簇的合并），则该组即为一个社区。所有最优簇的集合称为 Pmax。接下来，该算法验证整个网络图是否具有社区结构。为此，它计算 z‐score，即相对于等价零模型图集合中具有局部模块度最优的划分的平均模块度，Pmax中划分的平均模块度的z‐score。相对于阈值较大的 z‐score 表明存在有意义的社区结构。一旦发现有意义的社区结构，便通过最小化表示连通顶点到对角线的平均距离的代价函数，将亲和性矩阵变为近似块对角形式。这些块对应于社区，恢复出的划分代表最高层次的组织结构。

为了确定较低层次，对上一层次识别出的每个子图迭代执行该过程，并将其视为独立的图。当所有找到的块均不具有相关簇结构（即其z‐score 低于阈值）时，过程停止。该方法生成的划分在构造上是层次化的，因为每一层次的社区都嵌套于更高层次的社区之中。然而，该方法可能找不到任何相关划分（无社区结构）、仅找到单个划分（有社区结构但无层次），或找到多个层次，在这方面优于大多数现有方法。该算法并不快速，因为模块度局部最优的搜索以及相似性矩阵的重排均采用模拟退火实现，但对于计算机生成网络能给出良好结果，对某些真实网络也能给出有意义的划分。

在2008年 ，克劳塞特等人提出了一种生成层次化随机图类别的算法。他们通过树状图D（即层次结构的自然表示）以及与树状图的n −1个内部顶点相关联的一组概率 {pr} 来定义一个层次化随机图。顶点i的祖先是指从 “叶”顶点i出发并一路向上到达树状图顶端过程中所经过的任意内部顶点。顶点i和j之间存在链接的概率由i和j的最低公共祖先对应的概率 pr 给出。克劳塞特等人使用贝叶斯推断作为效用函数，搜索最符合观测到的图拓扑的模型（D,{pr），该模型拟合图的概率与似然成正比：

$$
L(D,{pr})=\prod_{r\in D} P E r L r R r -E r \tag{12.1}
$$

这里，Er表示连接其最低公共祖先为r的顶点的边数，Lr和Rr分别表示从树状图顶点r出发的左子树和右子树中的图顶点数量，乘积遍历所有内部树状图顶点。对于给定的树状图D，最大似然L(D)对应于概率集合{pr}，其中pr 等于两个子树之间边的实际密度Er/(LrRr)。可以通过将每个模型图(D, {pr})赋予正比于最大似然L(D)的概率，来定义描述给定图G的层次化随机图统计系综。该系综可通过马尔可夫链蒙特卡洛方法进行采样。克劳塞特等人提出的方法似乎在大约O(n2)的时间内收敛到平衡态，尽管实际复杂性可能高出很多。尽管如此，作者仍能够研究包含数千个顶点的图。从平衡状态下采样的足够大的模型构型集合中，可以计算模型的平均性质，例如度分布、聚类系数等，并将其与原始图的相应性质进行比较。在真实图上的测试表明，该模型确实能够很好地描述图的性质。此外，该模型还能预测原始图中顶点之间的缺失连接。这是一个由利本‐诺维尔和克莱因伯格在2003年提出的重要问题。此处真实图的边来源于观测/实验，这些观测/实验可能未能发现系统单元之间的某些关系。从层次化随机图系综中，可以推导出所有图顶点对之间的平均连接概率。通过对原始图中未连接的顶点对所对应的概率进行排序，可以预期具有最高概率的顶点对很可能在系统中存在连接，即使这些连接未被观测到。克劳塞特等人指出，他们的方法并不能为给定图提供明确的层次结构，而是一类具有明确定义概率的可能组织结构。显然可以合理地假设许多结构都与给定的图拓扑相容。在社区结构的情况下，尚不清楚从层次化随机图系综的平均操作中能提取哪些信息。此外，由于层次结构由树状图表示，因此无法根据相关性对划分进行排序。事实上，克劳塞特等人的工作质疑了“相关划分”的概念，并在科学界引发了关于图聚类本身含义的讨论。

如Girvan和Newman以及其他学者对分裂式层次方法的研究所示，中心性与介数的结合为网络社区检测提供了一个良好的层次判别器。然而，该方法在大规模网络上可能具有较高的计算密集型。将层次化方法作为集成方法的一部分可能具有价值，其中网络社区检测方法所得出的图可形成一个缩减规模网络。但目前文献中针对结合该技术的集成方法的研究较为稀少。

12.3.1.2 凝聚方法

以凝聚法方式识别社区的层次算法曾是最流行的基于层次的方法，但由于分裂方法最近的流行，这一点如今已存在争议。有些算法在其方法中包含了凝聚法特性，但其核心方法是其他技术。例如2004年的格瓦和纽曼算法（克劳塞特等人2004年），该算法基于模块度优化，将在后续讨论。尽管这些技术目前很流行，但仍有一些现有算法使用凝聚法进行社区发现。

霍普克罗夫特等人于2004年研究了动态社区检测问题。作者分析了由 NEC CiteSeer数据库生成的引用图的时间快照，时间范围覆盖了1990年至 2001年。该方法中用于比较顶点的相似性度量基于余弦相似度，这是一种在信息检索中广泛使用的度量方法。每个快照中识别出的自然社区被定义为： 在图中仅因少量顶点及其边被移除（即微小扰动）而受到轻微影响的层次树中的社区。作者通过寻找不同快照之间最佳匹配自然社区，从而追踪社区的历史演变，特别是观察到新社区的出现，对应着新研究主题的产生。该方法的主要缺点在于使用了层次聚类，无法从包含多种图划分的层次树中分离出有意义的社区。

在 2005年，巴格罗和博尔特提出了一种称为L‐壳的方法。该方法用于寻找任意顶点的社区。社区是基于一个简单准则在局部定义的，该准则涉及顶点组内部和外部的边的数量。该过程从一个起始顶点开始，不断添加位于连续壳层上的顶点，其中壳层被定义为与起始顶点具有固定测地距离的一组顶点。第一层壳包含起始顶点的最近邻，第二层包含次近邻，依此类推。在每次迭代中，计算新一层顶点与当前簇内部和外部顶点之间的连接边数。如果这两个数值的比值（外向度）超过某个预定义阈值，则将新壳层的顶点加入当前簇，否则过程停止。通过扩展壳层来闭合社区的思想早在一年前由科斯塔（MacKay1995）提出。在那里，所有壳层都以枢纽为中心。然而，在该方法中，簇的数量是预先指定的，且每个簇最多只能包含一个枢纽。由于该过程具有局部性，L‐壳方法非常快速，能够迅速识别社区。遗憾的是，该方法仅当源顶点与其社区边界大致等距时效果良好。为了克服这一问题，巴格罗和博尔特建议从每个顶点出发重复该过程，并生成成员矩阵M：若顶点 j属于顶点i的社区，则矩阵元素Mij为1，否则为0。可以通过根据相互距离适当地排列行和列来重写成员矩阵M。之间的距离

两行（或列）之间的差异定义为元素不同的条目数量。如果图具有清晰的社区结构，成员矩阵将呈现块对角形式，其中各个块标识出社区。该方法能够检测社区间的重叠。然而，由于需要重新排列矩阵，这种方法速度较慢，计算时间复杂度为O(n3)。2007年，罗德里格斯等人通过改进巴格罗和博尔特算法，提高了计算效率，该改进算法单独考察边界顶点，并同时分析运行中的社区的第一和第二最近邻（罗德里格斯等人 2007年）。

在 2009年，安等人提出了一种称为层次化链接聚类的凝聚方法。他们在此使用了一种针对一对相邻边的相似性度量，该度量表示非重合端点的邻居集合之间重叠部分的大小，除以这些端点的不同邻居总数。边的组按相似性降序成对合并，直到所有边都处于同一簇中。最终生成的树状图提供了关于图的社区结构的最完整信息。然而，与通常情况一样，其中大部分信息是冗余的，并且是该过程本身的产物。因此，安等人引入了一个用于选择最有意义划分的质量函数，称为划分密度，其本质上是簇内边密度的平均值。该方法能够在生物网络（如蛋白质‐蛋白质网络和代谢网络）以及手机通信的社交网络中发现有意义的簇。它还可以扩展到多部图和加权图。

王等人在2011年提出了一种较新的算法。该算法基于作者之前提出的方法，即HC‐PIN算法。该算法基于此处定义的边聚类的一种改进版本：

$$
CC= \frac{|Ni \cap Nj|}{\min(di, dj)} \tag{12.2}
$$

Ni和di分别是顶点i的邻居列表和度。根据该算法，首先计算所有边的边聚类系数值，并按降序排序。然后按照边聚类系数值的降序，通过这些边将单点合并在一起。该算法的问题在于，如果在某个PIN中，一个良好的簇内部没有三角形或存在环，则边聚类系数公式会为该簇内部的边产生较低的值。因此，FAG‐EC算法无法生成准确的社区。该新算法引入了一种称为边聚类值（ECV）的度量，定义如下：

$$
ECV= \frac{||Nu \cap Nv| |Nu| |N||Nu \cap Nv| |Nu| |N||Nu \cap Nv| |Nu| |N|2|}{||Nu \cap Nv| |Nu| |N||Nu \cap Nv| |Nu| |N||Nu \cap Nv| |Nu| |N|v||} \times \tag{12.3}
$$

Nu 是顶点 v 的邻居集合。该方法解决了先前社区簇不准确的问题，但仍存在无法识别重叠社区的问题。

总体而言，层次化算法在分析网络时是一种有效的方法，特别是当期望的结果包含由相似顶点组成的社区时。许多

较新的算法（如我们讨论的那些）提供了解决某些缺点的方法，但在每种情况下，都会在准确性或复杂性方面存在缺点。

所有层次化算法都有一个优势，即无论分析意图如何，它们都不需要预先了解社区的数量和规模。这对于具有不同规模社区的网络尤其有用，因为用于估计社区数量和规模的方法通常会将顶点划分为规模相等的社区（ Orman 等人，2012）。然而，其权衡之处在于凝聚技术的可扩展性较差。

如果使用距离作为相似性度量，则单个顶点到顶点链接的计算复杂度为 O(n2)，整个图的计算复杂度为 O(n2 log n)。这意味着当距离未被先验定义且网络具有现实世界规模时，这些算法的计算复杂度可能变得非常高，并因相似性度量计算的计算开销而进一步加剧（基于密度的收缩 2011）。

12.3.1.3 基于层次的算法，给定分析意图

基于类别的 对于基于类别的分析，层次化社区发现是一种有效的顶点划分方法。由于社区是通过相似性定义的，顶点会自然地围绕该相似性度量聚集到各个类别中。当然，相似性度量的选择（例如余弦、杰卡德、马哈拉诺比斯等），以及所使用的度量方式（例如介数、中心性、其他定量特征等），还有它们在分析中的匹配程度，都会显著影响结果和性能。在面向类别的分析意图下，基于层次的方法的一个主要弱点是，在类别内部的顶点之间，除了单一的相似性度量外，缺乏上下文上的区分能力。这意味着在一个社区内部，无法判断哪个顶点最重要，或其如何与社区外部的顶点相关联。

基于事件的 研究文献中关于使用层次化方法对网络社区进行基于事件的分析的优势讨论较少。这是因为顶点之间的物理或通信定义的连接并不是社区构建的先决条件。考虑连接的层次化方法通常具有分裂法的性质，会移除那些位于顶点之间且处于社区间边界的链接。连接仅在顶点基于相似性被聚类后才被考虑，因此链接并不是决定顶点属于某个社区的主要因素。此外，在凝聚法层次化方法中，连接根本不是影响因素。

12.3.2 基于空模型的方法

零模型是与相应图在某些结构上相匹配的随机图。在空模型算法中，顶点连接中有一定比例位于

在原始/对应图中属于同一社区由以下公式表示：

$$
\frac{1}{2m}\sum_{ij\in v}[A_{ij}]\delta(c_i, c_j) \tag{12.4}
$$

以下公式用于推导具有与原始/对应图相同度分布的随机图中顶点连接的期望比例。

$$
\frac{1}{2m}\sum_{ij\in v}\left[\frac{k_i k_j}{2m}\right]\delta(c_i, c_j) \tag{12.5}
$$

纽曼和吉尔凡在2004年 提出的算法是首个使用零模型方法的算法。该方法中，零模型网络的连接（边）在保持度和顶点数量与原始/对应图相同的约束下随机重连；本质上是利用来自原始/对应图的约束来实施零模型。

使用零模型是模块度优化网络社区检测技术背后的基本概念，其中零模型代表不同的网络连接配置。配置模型描述了一个具有n个顶点的网络，其中每个顶点m的度值为Dm。在配置模型中，由边表示的每条通信被分成两半，每一半称为一个存根，并在全局网络中与其他任意存根（包括其自身）随机重连。当使用模块度来发现社区时，原始图中顶点组内部的边数必须超过相应零模型中同一顶点组内部边的期望数量，该期望值是零模型所有可能的重连实现的平均值。

2009年，Shen 等人提出了一种尝试使用零模型检测重叠的方法。他们在此提出了如下定义：

$$
Q= \frac{1}{2m}\sum_{ij} \frac{1}{O_i O_j}\left( A_{ij} - \frac{k_i k_j}{2m}\right)\delta(C_i, C_j) \tag{12.6}
$$

Oi是包含顶点i的社区的数量。每条边对模块度的贡献则越小，其端点所属的社区数量越多（Shen 等人，2009年）。

另一种基于空模型的算法由Nicosia等人在2009年提出，用于解决重叠社区问题。他们从通用表达式出发，研究了有向无权网络：

$$
Q_{ov}= \frac{1}{m} \sum_{c=1}^{n_c} \sum_{i,j}\left[ r_{ij}^c A_{ij} - s_{ij}^c \frac{k_{out}^i k_{in}^j}{m}\right] \tag{12.7}
$$

k in i 和 k out j 分别是顶点i和j的入度和出度，索引c标记社区且r i j c= s i j c= δ c i c j c，其中 c i和 c j对应于

社区i和j。在这种情况下，只有当ci= cj时，边ij才会对求和有贡献，这与模块度的原始定义一致。对于重叠社区，顶点i和j的成员系数分别为ai, c, aj, c。我们也可以假设 rijc= F(ai, caj, c)，其中F是某个函数。项sijc与模块度的零模型相关，必须谨慎处理。在模块度的原始零模型中，边是通过连接两个随机存根形成的，因此需要定义随机存根在各个社区中的成员关系。如果我们假设任意两个顶点的成员系数之间先验没有相关性，则可以将来自社区 c中顶点i的一个存根赋予对应于所有可能与i形成的边的平均成员系数。在有向图上，我们必须区分出存根和入存根，因此需要

$$
\beta_{i\rightarrow,c}^{out} = \frac{\sum_j F(\propto_{i,c},\propto_{j,c})}{n} \tag{12.8}
$$

$$
\beta_{i\leftarrow,c}^{in} = \frac{\sum_j F(\propto_{j,c},\propto_{i,c})}{n} \tag{12.9}
$$

其中 α是i在c中的隶属关系，且可写出模块度的以下通用表达式

$$
Q_{ov}= \frac{1}{m}\sum_{c=1}^{n_c}\sum_{i,j}\left[ r_{ij}^c A_{ij}- \frac{(\beta_{i\rightarrow,c}^{out} k_{out}^i)(\beta_{j\leftarrow,c}^{in} k_{in}^j)}{m} \right] \tag{12.10}
$$

现在问题变成了函数 F (∝i, c, ∝j, c) 的选择。如果上述公式要作为模块度在重叠社区情况下的扩展，则其必须满足经典模块度的一般性质。例如，将整个网络作为一个单一簇时，模块度值应为零。结果表明，许多类函数都能得到满足此要求的模块度表达式。否则，F 的选择相当随意，只能根据优化结果进行事后检验。帕帕多普洛斯等人于 2009 年提出了一种类似的方法，称为桥接限定（Papadopoulos et al. 2009年）。两种方法的主要区别在于，此处围绕一个顶点的簇会不断增长，直到遇到边界边为止。

除了模块度优化之外，基于空模型的算法示例由赖希哈特和博恩霍尔特在2006年提出。在此，作者表明可以将社区检测问题重新表述为寻找自旋玻璃模型基态的问题。其中每个顶点由一个波茨自旋变量 σi标记，该变量指示包含该顶点的簇。该模型的基本原理是：边应连接同类（即相同自旋状态）的顶点，而不同类（即不同自旋状态）的顶点之间应未连接（理想情况下）。因此，必须在能量上鼓励同一类顶点之间的边以及不同类顶点之间的非边，同时惩罚不同类顶点之间的边以及同类顶点之间的非边。由此得到的自旋模型的哈密顿量为：

$$
H({\sigma})= -\sum_{i<j} J_{ij} \delta(\sigma_i , \sigma_j )= -\sum_{i<j} J(A_{ij} -\gamma p_{ij} ) \delta((\sigma_i , \sigma_j )) \tag{12.11}
$$

其中J是表示耦合强度的常数， Aij是图的邻接矩阵的元素， γ> 0是表示现有边和缺失边对能量相对贡献的参数，pij是在具有与所考虑图相同总边数 m的零模型图中连接i和pij的期望链接数，以及连接i和j的期望链接数。该系统被视为自旋玻璃，因为自旋之间的耦合既包括铁磁性（在图的边上，当 γpij < 1时）也包括反铁磁性（在未连接的顶点之间，因为Aij= 0和 Jij=–J γpij< 0）。乘法常数J在实际应用中无关紧要，因此在下文中我们设J= 1。自旋‐自旋相互作用的作用范围是无限的，因为任意一对自旋之间都存在非零耦合。需要注意的是，尽管此方法类似于模块度，但由于零模型和参数 γ 均可任意选择，因此该方法比模块度通用得多。

巴伯等人在2008年（Danon 等人 2005）提出了一种用于识别二分图中社区的算法。这里假设两个顶点类（红色和蓝色）分别由 p 个和 q 个顶点组成。红色顶点 i的度用 ki表示，蓝色顶点 j的度用 dj表示。图的邻接矩阵 A 呈块非对角形式，因为边仅存在于红色顶点和蓝色顶点之间。因此，巴伯假设零模型矩阵 P也具有块非对角形式，其中元素 Pij通常表示零模型中顶点i和 j之间的期望边数：

$$
P= \begin{bmatrix} O_{p\times p} & \bar{P} {p\times q} \ \bar{P}^T {q\times p} & O_{q\times q} \end{bmatrix} \tag{12.12}
$$

其中O是所有元素均为零的方阵， $\bar{P}_{ij}= \frac{k_i d_j}{m}$与标准模块度的零模型中的定义相同（尽管也可以有其他选择）。根据Barber的说法，模块度的谱优化对于二分划分类问题能给出极好的结果，但当簇的数量未知时，其性能会下降，而这种情况通常是常见的。

基于零模型的算法所存在的分辨率极限问题已有充分记录。通常，许多具有社区结构的图包含大小各异的社区（Palla 等人 2005；克劳塞特等人 2004； Guimera 等人 2003）。如果两个小型子图恰好通过少量虚假边连接，即使它们彼此无关，模块度仍会将它们归入同一簇。如前所述，问题在于零模型本身及其隐含假设，即每个顶点可以与所有其他顶点相互作用，这意味着图的每一部分都知晓其他所有部分，而实际情况并非总是如此。更合理的假设是，每个顶点仅对整个图有有限的视野，并仅与局部的小范围部分发生交互。已有若干算法针对此问题进行了研究，例如 Li 等人（2008）；Fortunato 和 Barthelemy（2007）； Ruan 和 Zhang（2008）；以及 Berry 等人（
2009）。在 Berry 等人的研究中，考虑了加权图，其中簇内边的权重为 1，簇间边的权重为∈。他们得出结论：若满足以下条件，则内部强度为 ws的簇可能无法被检测到

$$
w_s< \sqrt{W\varepsilon/2} - \varepsilon
$$

其中W是图的总强度。因此，当 ε减小时，分辨率限制也随之降低。作者利用这一结果表明，通过对给定的无权图的边进行适当的加权，仍然可以使用模块度优化来检测具有很高分辨率的簇。

尽管Berry等人提出的算法在缓解分辨率极限问题方面显示出一定的潜力，但这一弱点仍然存在。该领域的研究仍在持续进行中。由于这一问题，基于模块度优化的方法在尝试根据观测到的事件识别社区时，效果至多只能达到中等水平。由观测到的事件构建的社区往往在规模上有所差异，而使用当前模块度优化所提供的选项时，不可避免地会丢失其中一些社区。当分析意图是基于类别的时，该方法可能产生积极的结果。这是因为许多模块度优化技术与层次聚类方法相结合，能够自然地将顶点划分为类别相似的簇。唯一需要考虑的问题是检测准确性与计算速度之间的权衡，因为许多更精确的技术使用了模拟退火等全局优化技术，而这些技术通常非常缓慢。

由于高度的置换性，零模型算法能够提供可靠的结果，这也解释了为何许多网络社区检测算法在某种程度上使用模块度。尽管这类算法广受欢迎，但也存在一些缺点。一个众所周知的问题是分辨率限制，这使得模块度难以发现小社区。零模型方法存在内在问题，因为其方法论涉及将原始图与零模型图之间的连接数进行比较。零模型图假设每个顶点可以连接到网络中的任何其他顶点，但如果网络规模较大，这一假设就不合理，无法反映现实情况。从实际角度来看，随着网络规模增大，两组顶点之间的预期连接数会减小。如果网络足够大，这两组顶点之间的预期边数可能小于1，从而导致模块度值偏高。这会造成定义出原本不存在的包容性社区，因为算法会将这两组顶点合并，即使它们本不应被合并。由于较小的顶点组总会被不断合并，小社区可能永远无法被发现。在文献中已提出多种方法来解决此问题，这些方法将在本文后续部分进行讨论。

12.3.2.1 基于空模型的算法，给定分析意图

基于类别的 零模型方法在识别网络社区以满足基于类别的分析意图方面可能有效。然而，前提是选择了一个能够区分类别的适当度量。由于零模型方法会利用所有可能的顶点连接，如果该度量能够区分社区，则甚至不存在的边也可能被检测为社区的一部分。

基于事件的 基于零模型的算法通常在基于事件的分析背景下能有效识别出规模相等的社区。然而在此上下文中，它们通常难以较好地检测小社区。在基于观测事件进行分析时，识别大社区和小社区都非常重要，因此空模型算法可能并非此类分析的理想单一选择。与层次化算法类似，空模型方法在此背景下可与其他算法形成互补。由于其可能具有较高的计算成本，在集成网络社区检测配置中，应尽可能在网络规模缩减技术之后再应用空模型方法。

12.3.3 基于统计推断的算法

基于统计推断的网络社区检测算法旨在从一组观测数据出发，推导出网络社区的特性，以验证顶点之间如何（或预期如何）相互连接的假设。使用该技术的算法通过尝试找到最适合观测数据生成图的模型来识别社区。与其他统计技术类似，该模型假设顶点根据观测中可获得的某些特征具有某种分类。在网络社区检测的上下文中，该方法由MacKay（1995）进行了详细阐述。MacKay的工作是将信息论与机器学习相结合以描述网络社区检测中通信过程的开创性工作。因此，文献中许多后续方法都建立在MacKay方法的基础之上。

由于存在多种类型的统计推断，因此有几种算法使用此类统计方法，例如贝叶斯推断（Morup和Schmidt 2012）、块建模（Karrer和Newman 2011）、模型选择（层次化块结构 2014）以及广义信息论（MacKay 1995）。贝叶斯推断利用观测数据来估计某个假设为真的概率。块建模将图分解为具有共同属性的顶点类别。顶点通常被分组为结构等价或规则等价的类别。当两个或多个顶点具有相同的邻居时，称它们具有结构等价性。当某一类别的顶点与另一类别的顶点具有相似的连接模式时，则称为规则等价。模型选择顾名思义，就是应用多个模型（假设）并对可观测数据进行评估以找到最佳匹配。在信息论算法中，所发现的社区被视为对整个图的压缩描述。

所有使用此方法的算法都有一个优势，即能够直接解决统计显著性问题。这是因为社区的聚类是基于顶点及其连接链接所表现出的统计特性。

使用基于推理的社区检测方法的研究历史不如其他方法悠久，但最近已引起广泛关注。在本节中，我们将重点关注几种最近流行的方法。这些方法包括基于贝叶斯、模块建模、模型选择和信息论的方法。

2008年，霍夫曼和威金斯提出了一种基于贝叶斯的社区检测方法。他们在此将具有社区结构的图建模为planted partition problem（种植划分问题），即同一簇内顶点之间存在边的概率为θc，不同簇间顶点之间存在边的概率为 θd（霍夫曼和威金斯 2008年）。未观测的社区结构由顶点的标签集合→σ表示； πr再次表示第r组中顶点所占的比例。共轭先验分布 p(θ)和 p(π)被选择为贝塔分布和狄利克雷分布。在给定矩阵A的情况下，最可能的簇数量 K∗使条件概率p({K|A})达到最大，即存在K个簇的概率最大。此处，霍夫曼和威金斯假设簇数量的先验概率 p(K)是一个平滑函数，因此最大化 p({K|A})等价于最大化贝叶斯证据 p{A|K} ∝ p(K|A)/p(K)，该证据通过对可分解的联合分布p(A,σ| π,θ, K)关于模型参数θ和π.进行积分得到。这种积分仅在小规模图上可以精确完成。该算法的复杂性估计为 O(n∝)，在合成图上的测试使用了 ∝= 1.44。此处高复杂性的主要原因在于较高的内存需求。这种方法非常强大，因为它不需要在分析开始前预先知道簇的数量，也不需要猜测边的概率，而是通过算法过程推断得出。

另一种更新的基于贝叶斯的方法由普索拉基斯等人于2011年提出（ Psorakis 2011）。在这里，作者提出了一种称为贝叶斯非负矩阵分解的算法。其中NMF代表非负矩阵分解。它是一种机器学习中的特征提取和降维技术，已被应用于社区检测。NMF在非负性约束下将近似地将特征矩阵V分解为两个矩阵，即 V ≈ WH，其中V是 n × m，W是n × k， H是 k × m，而k是由用户提供的社区数量。W表示在降低维度后的特征空间中的数据。归一化W中的每个元素wi,j量化了顶点i相对于社区j的依赖程度。在普索拉基斯等人提出的算法中，矩阵V（其每个元素Vij表示发生在两个顶点i和j之间的交互次数）通过NMF进行分解，作为生成模型参数推断的一部分。该方法的一个问题是，传统上由于矩阵乘法的存在，非负矩阵分解在时间和内存限制方面效率较低。在普索拉基斯等人使用的版本中，最坏情况下的时间复杂度为 O(kn2)，其中k表示社区的数量。

Airoldi 等人于2008年提出了一种基于模块建模的方法。该方法中，作者引入了混合成员关系的概念。该技术将邻接矩阵分解到低维空间，以表达顶点块之间的有向社会关系模式。根据生成过程，对于每一对顶点，分别对源和目标的组成员关系进行采样：链接是通过从二项分布中采样生成的，该分布编码了在所考虑的组。由于成员分配是针对每个可能的链接独立进行的，因此用户可以属于多个组。

在巴尔比耶里于2013年提出的一种近期方法中，作者介绍了一种社区检测算法，该算法将随机生成块模型拟合到观测到的社交图谱以及一种称为级联的度量上（2013）。一个项目i的级联是一系列（用户，时间戳）对，记录了哪些顶点采用了i以及采用的时间。在CCN模型中，每次观测都被假设为一个随机过程的结果，其中给定用户u根据一组主题/社区在网络中进行活动，这些主题/社区也代表了用户兴趣。对于给定社区c，用户u对该社区的参与度由两个参数决定： π c, su和 π c, du，其中π c, s u衡量用户u在社区c中的主动参与度，而 π c, du衡量用户u在社区c中的被动参与度。以推特为例，假设用户u使用微博平台关注三个特定兴趣：（i）网络科学与数据挖掘，（ii）巴塞罗那市，以及（iii）摇滚传奇布鲁斯·斯普林斯汀。在第一个主题上， u会主动发布内容，并利用平台与其他研究人员交流；而在另外两个主题上， u只是被动地倾听：为了获取信息，u关注那些能提供有关巴塞罗那事件的优质信息源的用户，以及那些在布鲁斯·斯普林斯汀相关话题上具有权威性的用户。通常，这些优质信息源拥有大量关注者，在某种意义上是有影响力的。在第二和第三个社区中，u可能会转发一些信息，但几乎不会产生原创信息。回到我们的参数，我们可以预期u在π c, su和π c, ds u .上都有较高值。毫不奇怪，u在第一个社区中有许多关注者，而在其他两个社区中几乎没有关注者。这是该模型背后的一个关键观察：u在某个主题上发布内容的可能性、该信息被进一步传播的可能性，以及u拥有对该主题感兴趣的关注者的可能性，三者之间存在强相关性。在该模型中，这些因素共同由参数 π c, s u.表示。类似地，他们用参数π c, du.来建模在某一社区中收到入弧的可能性以及被该社区中其他用户影响的可能性。这正是他们实现社交图谱与级联集合联合建模的方式。该算法另一个重要特点是，一个用户可以属于多个社区，但一条链接通常仅由一个唯一主题解释。这种重叠允许信息在多个社区之间共享。该算法在真实世界的数据集上进行了测试，结果准确但速度非常慢。学习时间缓慢的原因是：（i）更新方程δk u和 γ k v的计算负担极大；（ii）M步是一个改进步骤而非优化步骤。GEM过程通常比标准EM过程的收敛速度更慢：结果是学习阶段需要更多的迭代次数，且每次迭代的计算量都极为沉重。

另一种基于块模型的方法由陈等人于2013年提出，用于处理动态网络 （2013）。该算法的灵感来源于许多网络随时间变化的事实，例如IP网络甚至社交群体。在此方法中，作者引入了一个概念称为重叠时间社区（OTC）。在此类社区中，顶点在任意给定时间可以属于多个社区，且这些社区也可以随时间持续存在。该算法首先采用基于优化的方法进行OTC检测，具体步骤如下：

$$
\max_{{Y_t}} \sum_{t=1}^{T} f_{A_t}(Y_t)
$$
$$
\text{s.t.} \sum_{t=1}^{T-1} d_{A_{t+1}, A_t}(Y_{t+1}, Y_t) \leq \delta
$$
$$
Y_t \text{ represents a cover, } t= 1,…,T.
\tag{12.13}
$$

快照质量fAt(Yt)具有两个作用：（1）衡量覆盖 Yt反映网络 At的程度，即 Yt中编码的相似性水平与 At中观察到的相似性水平之间的接近程度；（2）防止算法过拟合，例如生成重复的社区或大量相互重叠的小社区。函数dAt+ 1, At(Yt+1, Yt)是一个距离函数，用于度量时间t+ 1和t时覆盖之间的差异。因此，上述公式中的第一个约束条件确保了覆盖随时间平滑演化。对该方法的测试表明，即使是很小的网络也能通过该算法的时间重叠能力被检测出来。总的内存空间复杂度为O(E+ nrT)。基于时间的总复杂度为：O(nr2T+Mr2E+ MnrT)。当簇的数量r有界时，空间和时间复杂度在E和nT上均呈线性增长，这被认为是非常高效的。该方法的局限性在于其所使用的效用函数来识别有效划分，本质上与模块度相同。正如我们之前讨论的，模块度存在明确的分辨率限制问题。

在2007年，罗斯瓦尔和伯斯特罗姆提出了一种基于信息论的方法，其中图的社区划分表示发送方传递给接收方的完整结构的综合Y，接收方试图从中推断出原始图拓扑X。最优划分对应于包含关于X最多信息的信号Y。这可以通过最小化给定Y时X的条件信息 H(X|Y) 来定量评估：

$$
H(X|Y)= \log\left[\prod_{i=1}^{q}\binom{n_i(n_i -1)}{l_{ii}/2}\prod_{i>j}\binom{n_i n_j}{l_{ij}}\right]
\tag{12.14}
$$

其中，q为簇的数量，n i表示簇 i中的顶点数量， l i j 表示簇i与簇j之间的边的数量。我们注意到，如果对q不施加任何约束，则在X=Y（H(X|X) = 0）这种平凡情况下，H(X|Y)达到最小值。该解不可接受，因为它相对于原始数据集并未实现信息压缩。因此需要寻找良好的压缩效果与足够小的信息量H(X|Y)之间的理想权衡。最小描述长度（MDL）原则为此问题提供了一种解决方案，其实质是最小化一个由H(X|Y)加上关于顶点数n、边数m和簇数q的函数所构成的目标函数。这里，发现的社区的质量是社区结构复杂性以及社区结构与整个图之间互信息的函数。最优的社区结构是使得表示社区结构所需的比特数与在给定社区结构下表示整个图所需的比特数之和最小的结构。这里的社区检测旨在找到使图的描述长度达到最小的社区结构，其中描述长度以比特数来度量。使用模拟退火进行优化。因此，罗斯瓦尔和伯斯特罗姆的方法速度较慢，应限于最多约104个顶点的图。然而，即使可能导致准确性下降，也可以使用更快的技术。根据研究结果，当社区由不同大小的成员构成时，该方法优于模块度优化。

罗斯瓦尔和伯格斯特伦还在2008年提出了一种基于信息论的算法，其目标是针对完整的邻接矩阵，寻找描述图上信息传播过程所需信息的最佳压缩方式（罗斯瓦尔和伯格斯特伦2008）。该方法采用随机游走作为信息传播的代理模型。通过两级描述的方式——即为图中的重要结构以及同一结构内的顶点赋予唯一名称，但在不同结构之间重复使用顶点名称——可以实现比简单地为所有顶点分配不同名称更紧凑的描述。这类似于地理地图中常见的做法：结构相当于城市，通常在不同城市中使用相同的街道名称，只要在同一城市内每条街道名称唯一即可。霍夫曼编码（罗斯瓦尔和伯格斯特伦2008）被用于命名顶点。对于随机游走而言，上述结构即为社区，因为直观来看，游走者会在这些社区内部停留较长时间，因此它们在信息传播过程中起着关键作用。图聚类将问题转化为如下编码问题：寻找使无限随机游走的描述长度最小的划分。该描述长度包含两项，分别表示随机游走在簇内和簇间的香农熵。每当游走者转移到不同的簇时，在描述中就需要使用该簇的码字，以告知解码器发生了转移。显然，如果簇之间分离良好，则随机游走者在簇间转移的频率较低，因此使用以簇为区域的地图是有利的，因为在随机游走的描述中，簇的码字不会被频繁重复，同时由于表示顶点所用码字长度有限，描述长度得以显著减少。相反，如果不存在定义明确的簇，或者划分不能代表图的实际社区结构，则划分中各簇之间的转移将非常频繁，使用地图的两级描述几乎无法带来任何收益。结合贪心搜索与模拟退火可实现描述长度的最小化。这一过程较为缓慢，与其他使用模拟退火的方法类似。

一种基于信息论的算法，由罗斯瓦尔等人在2009年应用于有向加权图。对于加权图的情况，采用随机跳转使用概率作为一种效用方法，以替代随机游走来保证遍历性。该方法得到的有向图划分与通过优化纽曼‐吉尔凡模块度算法的有向版本所获得的划分不同，因为该方法识别顶点之间的成对关系，而无法捕捉流。

12.3.3.1 基于统计推断的算法，给定分析意图

基于类别的 基于统计推断的算法可以说是根据类别识别社区的最佳方法，因为用于发现社区的信息已基于类别编码到图中。

基于事件的 专注于观测到的事件的社区，出于与类别意图相同的原因，也可以通过多种形式的基于统计推断的算法很好地发现，顶点或链接的元数据被编码，因此可在分析中使用。正因如此，我们能够发现有关社区内外连接语义的大量信息。这种方法的一个重要障碍是计算的复杂性，包括时间和内存需求。这类分析的速度可能相当慢，具体取决于分析所需的详细程度。

12.3.4 基于团的算法

使用团来发现社区的方法完全基于观测到的连接。在这里，社区由称为团的完全连通子图创建，其中单个团或多个极大团的组合构成一个社区。由于团能够识别社区内的重叠，这一特性在现实世界中的社区中自然存在（Palla 等2005），因此团方法往往内在地支持基于类别和基于事件的分析意图。许多基于团的方法受限于必须发现网络中的所有团，而这个问题已被证明是一个NP‐完全问题。

一种广泛使用的社区检测方法称为团渗透方法，该方法由Palla等人在 2005年提出。该算法通过首先识别网络中某个k值下的所有极大团，然后让这些团在相邻时相互渗透，从而以一种自然的方式构建社区。为了实现相邻，渗透的团必须共享k−1个顶点。例如，由三个顶点组成的团是一个三角形，而另一个团若要渗透到该三角形中，则必须至少拥有两个顶点。基于子社区的构建允许顶点共享，因此它们可能存在重叠。此外，即使某些顶点不属于相邻的k‐团，它们也可能是相连的。为了识别k‐团，算法必须维护一个团与团重叠矩阵O的条目，该矩阵是一个n c xnc矩阵， n c其中为团的数量。此处 Oij表示团 i和j之间共享的顶点数量。该方法的局限性包括复杂性涉及发现极大团，其数量随图的规模呈指数级增长，被认为是NP‐完全问题。作者指出，这一限制并未妨碍在某些相对大规模网络中的社区发现。由于稀疏图中最多包含105个顶点时团的数量有限，该算法也被认为相对较快。

团渗滤算法被莱曼等人在2008年扩展到二分图。这里引入了双团这一术语，作为一个子图Ka， b如果一类的a个顶点与另一类的b个顶点都相互连接。两个团Ka，b若共享一个团Ka−1,b−1，则它们是相邻的，而一个Ka，b团社区是从彼此通过相邻Ka，b团路径可达的所有Ka，b团的并集。再次强调，找出所有的双团是一个NP‐完全问题。这主要是因为双团的数量随着图的规模呈指数增长，与 k‐团的情况相同。

昆普拉等人在2008年引入了一种团渗滤方法的快速版本。在此算法中，图最初为空，边被逐个顺序添加。每当添加一条新边时，通过搜索插入边端点的邻接顶点子集中是否存在(k−2)团来检查是否形成了新的k‐团。需要构建一个图Γ ∗，其中顶点是(k−1)团，边则设置在对应于同一k‐团子图的(k−1)团顶点之间。在过程结束时，Γ ∗的连通分量对应于所寻找的k‐团社区。该技术的时间复杂度与图中k‐团的数量呈线性关系，因此在实际应用中可能会有很大变化。尽管存在这种可变性，SCP已被证明比CPM快得多。SCP相较于CPM的最大优势在于其对加权图的实现。SCP按权重递减顺序插入边，这使得算法只需应用一次，而CPM则需要多次应用。

12.3.4.1 基于团的算法，给定分析意图

基于类别的 团通过观察直接连接并构建称为团的完全连通子图来形成社区。该方法可以识别类别，但需要首先发现每一个团。如前所述，发现团在计算上是昂贵的，而其他方法则更为高效。

基于事件的 事件是一系列多个直接连接的结果。由于基于团的方法是由直接连接构建的，因此它们非常适合用于发现事件。

12.4 结论

每种被综述的算法/方法都有其优缺点，这些优缺点取决于分析意图。总体而言，当分析意图为基于类别时，层次化和基于模块度的方法表现最佳。这是因为这两种方法会根据选定的相似性形式或度量自然地将顶点分组为类别。基于团的方法非常适合基于事件的分析，因为社区是由观测到的连接构建的，而不是基于相似性。基于统计推断的算法在两种意图上都有效，具体效果取决于所选择的社区发现方法。总体而言，并不存在一种适用于所有情况的完美算法，因此为了获得最佳结果，必须首先明确预期的结果类型。

如前所述，社区检测方法的文献往往侧重于在某一特定上下文中使用基准数据集对算法进行评估。在本章中，我们强调了在选择最佳社区检测算法时，应将分析意图或多上下文作为决定性因素的重要性。例如，如果将基于空模型的算法与基于团的方法进行比较，当分析意图是发现类别时，基于空模型的算法可能表现优于基于团的方法；而当搜索由一系列事件构成的社区时，基于团的方法则可能表现更佳。基于这些原因，我们认为在选择社区检测方法的决策过程中，必须考虑分析意图。第6节的附录展示了一个所综述的社区检测算法/方法的网格表，其中每种算法都根据其满足特定意图标准的能力进行了评估。未来，我们将利用此列表开发针对当前分析意图量身定制的新算法。