利用朴素贝叶斯分类器实现手写数字的识别

利用贝叶斯分类器实现手写数字的识别

贝叶斯决策理论：

条件：类别数一定，𝜔_i,i=1,2,3,…c ;
已知类先验概率和类条件概率密度 𝑃(𝜔_𝑖), 𝑃(𝑥│𝜔_𝑖 ), 𝑖=1,2,…, 𝑐

贝叶斯决策：

两类情况：
i𝐟 𝑷(𝝎_𝟏 |𝒙)> 𝑷(𝝎_𝟐 |𝒙) then 𝒙∈𝝎_𝟏
if 𝑷(𝝎_𝟏 |𝒙)< 𝑷(𝝎_𝟐 |𝒙) then 𝒙∈𝝎_𝟐
多类情况：
if 𝑷(𝝎_𝒊│𝒙)=max(𝑷(𝝎_𝒋│𝒙) then"𝒙∈𝝎_𝒊 𝒋=𝟏,𝟐,…,𝒄

贝叶斯公式：

已知：𝑃(𝜔_𝑖), 𝑃(𝑥│𝜔_𝑖 ), 𝑖=1,2,…, 𝑐

MNIST数据库介绍：

Google实验室的Corinna Cortes和纽约大学柯朗研究所的Yann LeCun建有一个手写数字数据库，训练库有60,000张手写数字图像，测试库有10,000张数字图像


MNIST数据集下载地址

实验步骤

1.导入数据集并进行二值特征提取

数据集包括四部分：训练图像、训练标签（表示图像为哪个数字）、测试图像、测试标签
二值特征提取将图片进行分割处理转化为0，1数字信息，方便操作

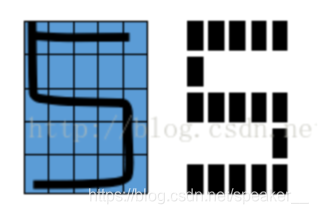
2.进行数据训练：

导入数据集后，利用训练图像和训练标签训练模型，模型的训练结果为：数字0-9出现的概率（𝑃(𝜔_𝑖)，代码中sum）、每个数字中图形二值化后和的概率（𝑃_j(𝜔_𝑖 ),代码中的shape）


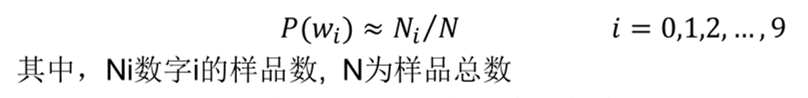
注：此处分子+1为了防止概率为0（拉普拉斯修正）

3.进行数据测试：

利用训练出的shape处理测试集中的图像，即：

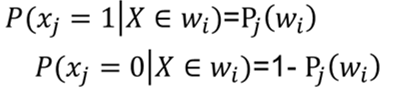
图像当前位置为1，乘以shape，为0时乘以1-shape，最后乘以该数字在训练集中出现的概率，可得到0-9个数字出现的概率，根据贝叶斯决策理论可得出概率大的数字即为当前数字
对比测试数据的label，判断该步测试是否准确

4.得出贝叶斯分类器进行数字分析的准确率

代码详解：

环境：Win10+pycharm+Anconda3（python 3.7）

import numpy as np
import struct
from collections import defaultdict


def normalize(data):  # 将图片像素二值化
    m, n = data.shape
    for i in range(m):
        for j in range(n):
            if data[i, j] != 0:  # 位置有像素即为1
                data[i, j] = 1
            else:
                data[i, j] = 0
    return data


def read_data():
    path = [r'C:\Users\19759\Desktop\data\t10k-images-idx3-ubyte',
            r'C:\Users\19759\Desktop\data\t10k-labels-idx1-ubyte',
            r'C:\Users\19759\Desktop\data\train-images-idx3-ubyte',
            r'C:\Users\19759\Desktop\data\train-labels-idx1-ubyte']  # 4个数据集路径
    data = defaultdict(dict)  # 声明一个空的字典 存放映射结果
    for i in range(0, 4):
        file = open(path[i], 'rb')  # 打开数据集
        f = file.read()
        file.close()
        # 以下进行数据的转化，图片、标签转化为数字信息
        if i % 2 == 0:  # 图片
            img_index = struct.calcsize('>IIII')
            _, size, row, column = struct.unpack('>IIII', f[:img_index])
            imgs = struct.unpack_from(str(size * row * column) + 'B', f, img_index)
            imgs = np.reshape(imgs, (size, row * column)).astype(np.float32)
            imgs = normalize(imgs)
            if i == 0:
                key = 'test'
            else:
                key = 'train'
            data[key]['images'] = imgs
        else:  # 标签
            label_index = struct.calcsize('>II')
            _, size = struct.unpack('>II', f[:label_index])
            labels = struct.unpack_from(str(size) + 'B', f, label_index)
            labels = np.reshape(labels, (size,))
            tmp = np.zeros((size, np.max(labels) + 1))
            tmp[np.arange(size), labels] = 1
            labels = tmp
            if i == 1:
                key = 'test'
            else:
                key = 'train'
            data[key]['labels'] = labels
    return data


def train(data):  # 训练模型
    imgs = data['train']['images']  # 打开训练集
    labels = data['train']['labels']
    # n为训练集的训练个数（6W） dimsnum为转化后保存图片的所需的0 1位数 labelnum为标签的个数（10个 0-9）
    n, dimsnum = imgs.shape
    n, labelnum = labels.shape
    # 初始化sum和shape
    sum = np.zeros(labelnum)
    shape = np.zeros((labelnum, dimsnum))
    for i in range(0, n):  # n个数据
        # 找出第i个中最大的下标 labels[i][j]=1代表第i张图片为数字j 其余为0
        pos = np.argmax(labels[i])
        # 该数字出现次数+1
        sum[pos] = sum[pos] + 1
        for j in range(0, dimsnum):  # 图片转化后的n个维度
            shape[pos][j] = shape[pos][j] + imgs[i][j]  # shape[pos][j]代表数字pos第j维1的和
    for i in range(0, labelnum):
        for j in range(0, dimsnum):
            shape[i][j] = (shape[i][j] + 1) / (sum[i] + 2)  # 将shape转化为概率
    sum = sum / n  # 将sum转化为概率
    return sum, shape


def test(data, sum, shape):  # 测试模型
    imgs = data['test']['images']  # 打开测试集
    labels = data['test']['labels']
    # n为测试集个数 dimsnum为测试图片转化后的位数（维度） labelnum标签个数（0-9十个）
    n, dimsnum = imgs.shape
    n, labelnum = labels.shape
    correct = 0  # 测试时根据训练模型准确的个数
    for i in range(0, n):
        pos = np.argmax(labels[i])  # 图片对应的数字pos
        maxx = 0  # 0-9中的最大概率
        vpos = -1  # 0-9中的对应最大概率的数字
        for k in range(0, labelnum):  # 数字0-9
            ans = 1
            for j in range(0, dimsnum):  # dimsnum维
                if imgs[i][j] == 1:  # 第i个图片的第j维对应为1 '出现此概率'
                    ans *= shape[k][j]
                else:  # 未出现
                    ans *= (1 - shape[k][j])
            ans *= sum[k]  # 乘数字k在训练集中的概率 理想状态下为0.1
            if ans > maxx:
                maxx = ans
                vpos = k
        if vpos == pos:  # 当找到的数字和测试集的数字相同 测试成功数+1
            correct += 1
    return correct, n  # 返回成功数和测试集总数


if __name__ == '__main__':
    data = read_data()
    sum, shape = train(data)
    correct, num = test(data, sum, shape)
    print("测试正确率为：", correct / num)

结果：

测试正确率为： 0.8413

注：本文为笔者记录学习专用，代码部分来自网络，注释内容为个人理解。

参考博客：https://blog.youkuaiyun.com/qq_36424540/article/details/89310529