计算机毕业设计hadoop+spark+hive高考推荐系统 高考志愿填报推荐推荐系统 高考数据分析可视化大屏 高考爬虫 高考分数线预测 数据仓库 大数据毕业设计

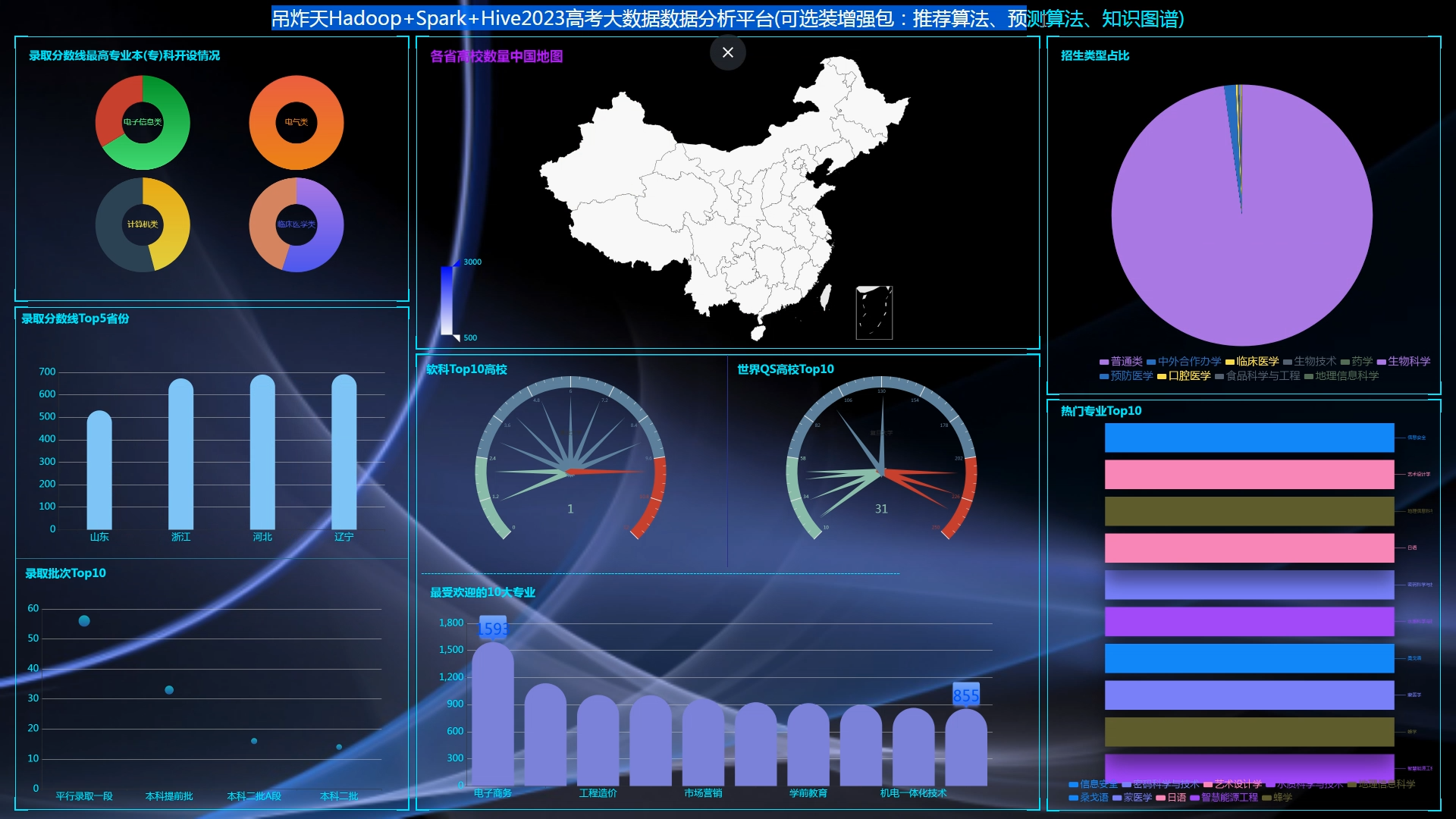
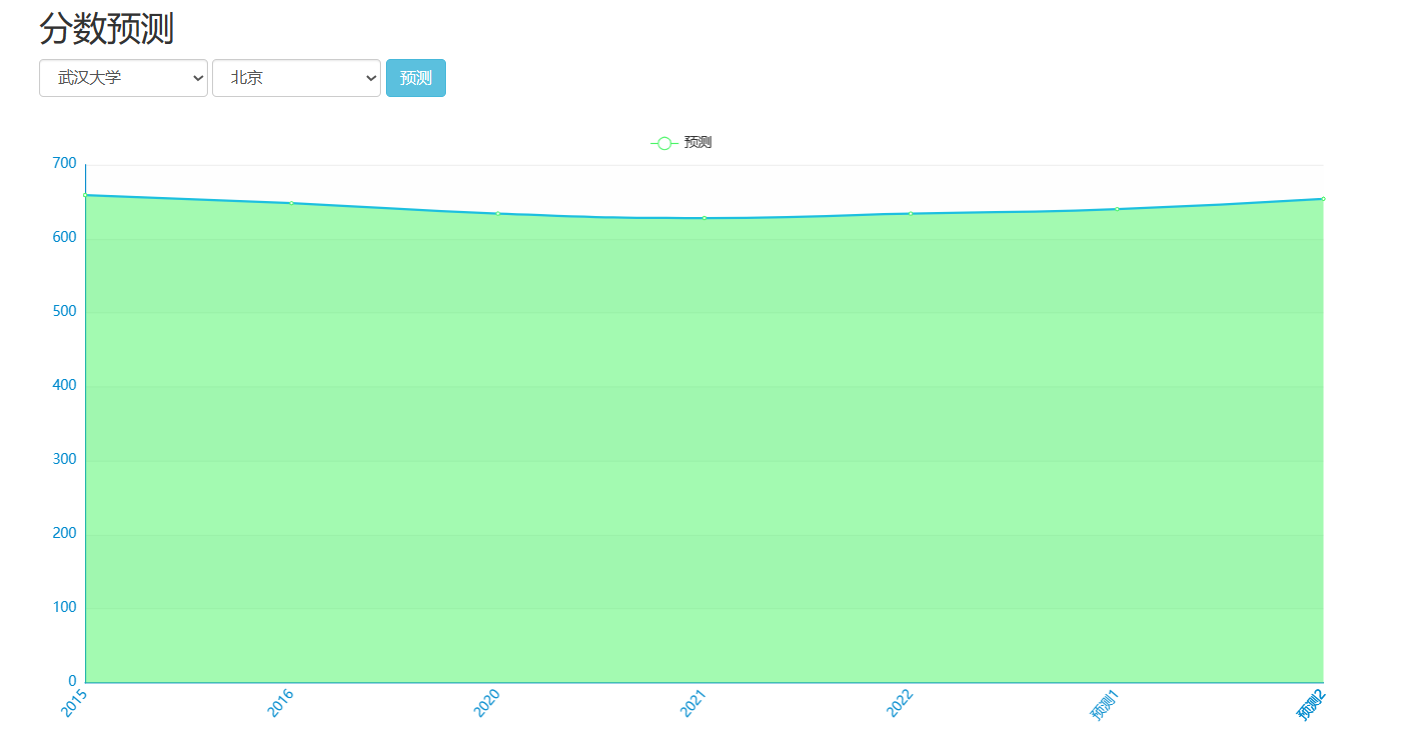
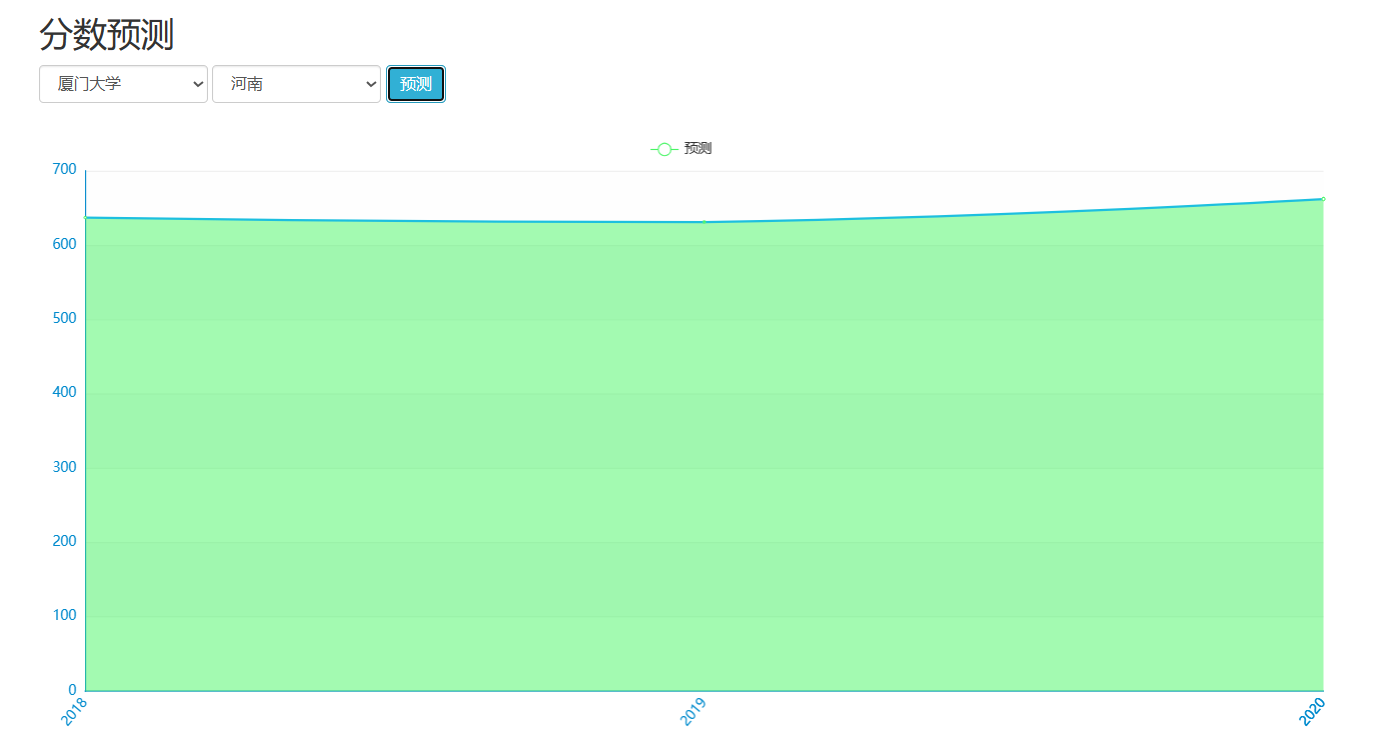
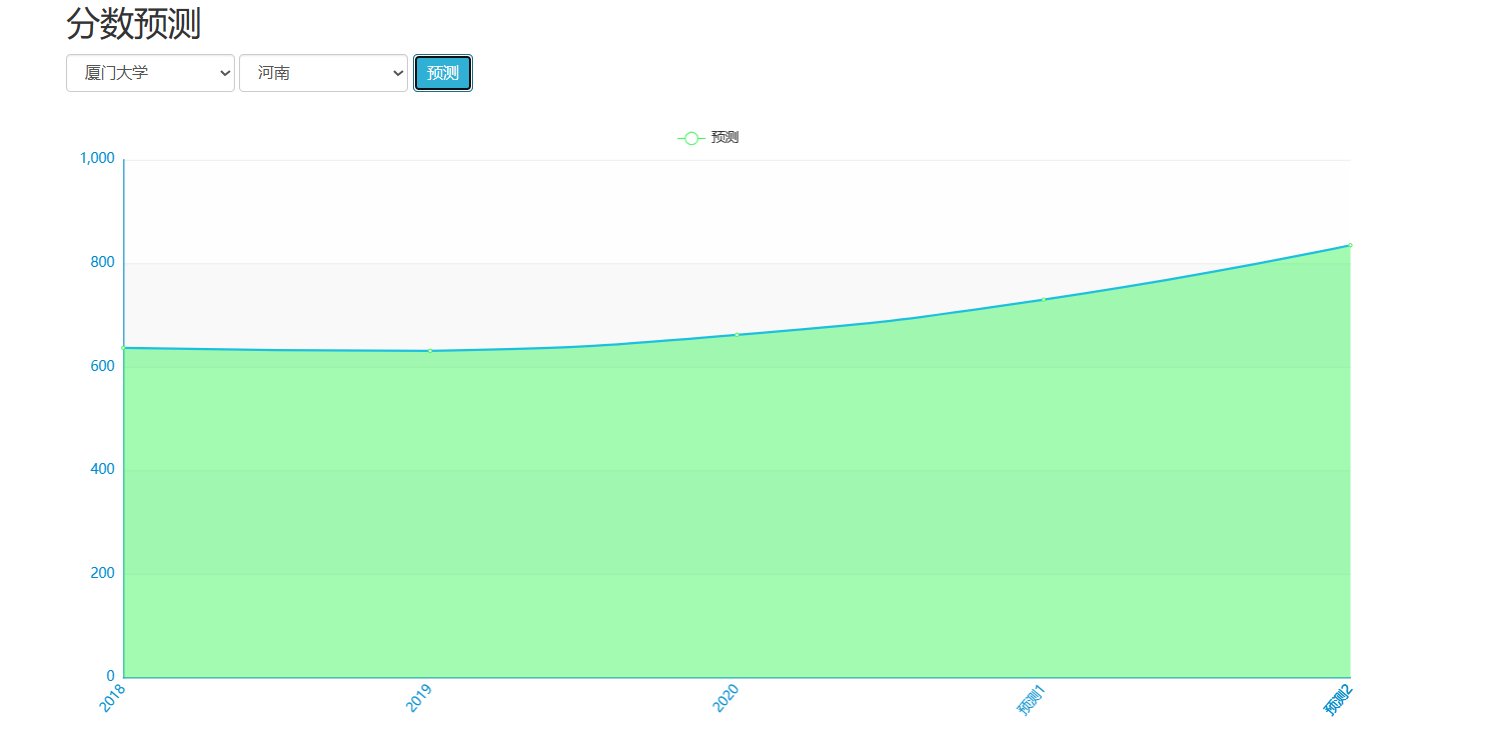
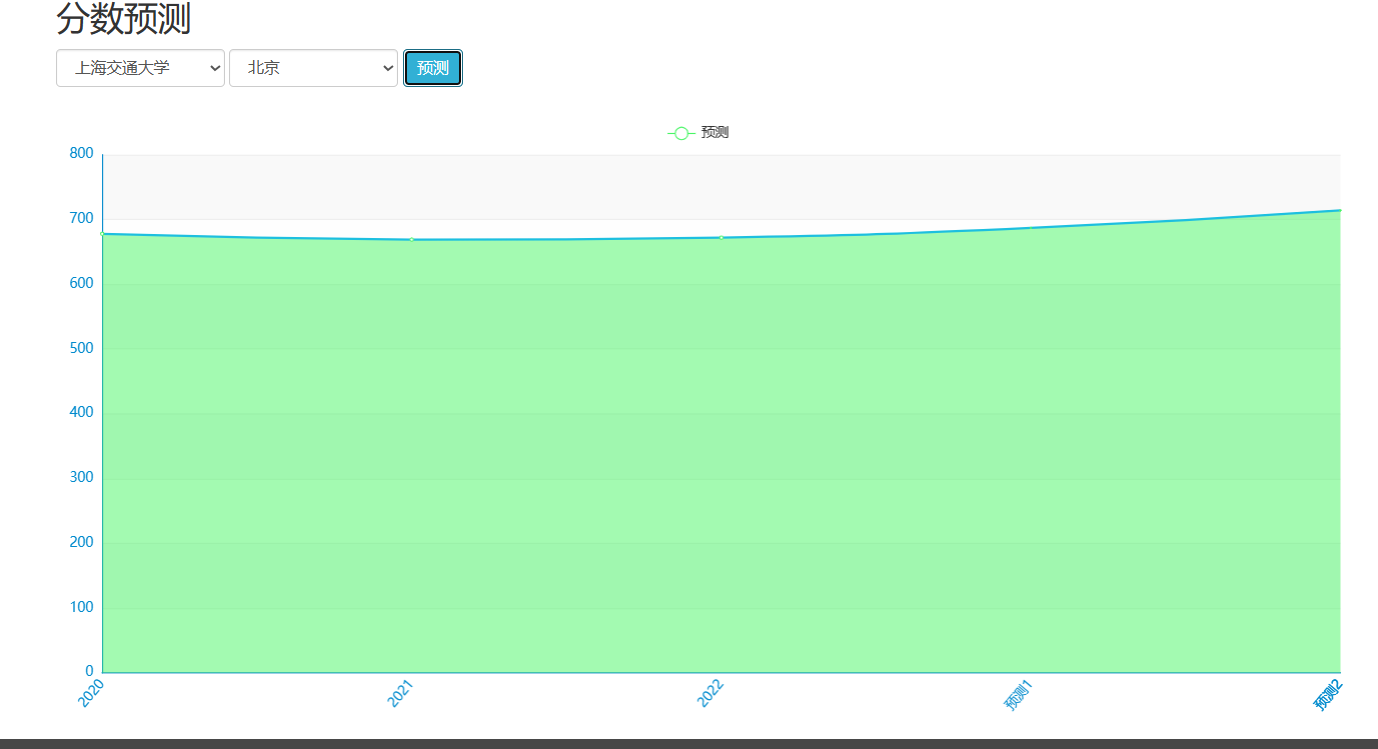
创建一个完整的CNN（卷积神经网络）来预测高考分数线是一个有趣的挑战，但需要注意的是，高考分数线的预测通常依赖于复杂的社会、经济和教育因素，而这些因素很难直接通过CNN从原始数据中提取。不过，如果我们假设有一些历史数据（如往年分数线、考生人数、学校录取情况等），并尝试通过简化的数据来模拟这个过程，我们可以构建一个简化的CNN模型。

但请注意，以下示例将使用模拟数据，并且CNN的应用在这种类型的数据上可能不是最优的。通常，对于这类预测任务，线性回归、随机森林或梯度提升机等模型可能更加适合。

下面是一个使用TensorFlow和Keras来构建CNN的示例代码，假设我们有一些基于年份和省份的模拟高考数据：

import numpy as np  
import tensorflow as tf  
from tensorflow.keras.models import Sequential  
from tensorflow.keras.layers import Conv1D, Dense, Flatten  
from sklearn.model_selection import train_test_split  
from sklearn.preprocessing import StandardScaler  
  
# 生成模拟数据  
# 假设我们有10年的数据，每年每个省份有1个数据点，特征维度为10（模拟的多种因素）  
np.random.seed(0)  
X = np.random.rand(10, 1, 10)  # 10年，1个省份，10个特征  
y = np.random.randint(500, 600, size=(10,))  # 假设分数线在500到600之间  
  
# 数据预处理  
scaler = StandardScaler()  
X_scaled = scaler.fit_transform(X.reshape(-1, 10)).reshape(X.shape)  # 因为是1D卷积，所以reshape回原形状  
  
# 划分训练集和测试集  
X_train, X_test, y_train, y_test = train_test_split(X_scaled, y, test_size=0.2, random_state=42)  
  
# 构建CNN模型  
model = Sequential([  
    Conv1D(32, 3, activation='relu', input_shape=(1, 10)),  # 输入形状为(样本数, 时间步数, 特征数)  
    Flatten(),  
    Dense(1)  
])  
  
model.compile(optimizer='adam', loss='mse')  
  
# 训练模型  
model.fit(X_train, y_train, epochs=100, verbose=1)  
  
# 评估模型  
loss = model.evaluate(X_test, y_test, verbose=0)  
print(f'Test MSE: {loss}')  
  
# 预测  
predictions = model.predict(X_test)  
print(f'Predicted Scores: {predictions.flatten()}')

重要说明：

1. 数据模拟：这里的X和y是随机生成的模拟数据，仅用于展示如何构建CNN模型。
2. 数据预处理：使用StandardScaler对数据进行标准化处理，这对许多机器学习模型来说都是很重要的步骤。
3. 模型结构：由于数据维度非常小（时间步数仅为1），这个CNN模型的结构非常简单。在实际应用中，可能需要更复杂的网络结构或考虑使用其他类型的模型。
4. 损失函数：这里使用均方误差（MSE）作为损失函数，因为它适用于回归任务。

请注意，上述代码仅用于教学目的，并且在实际应用中可能需要进行大量的调整和优化。