六阶无源正交信号网络设计

基于多相滤波器的六阶无源正交信号生成网络设计

摘要

本文提出了一种六阶无源正交信号生成网络的设计，用于验证无源多相滤波器在射频前端低中频收发器应用中的行为。该网络的传递函数基于叠加原理推导得出，具有两个最大值（频率分别为45千赫、100兆赫）和一个最小值（频率为2兆赫）。在1千赫至10兆赫的观测频率范围内，IQ失配出现在40千赫以下和2兆赫以上。

关键词 —叠加原理，正交信号产生网络，多相滤波器，低中频接收机。

I. 引言

复信号广泛应用于无线通信系统中的调制、解调以及频率上下变频器[1]中。因此，无源多相滤波器被广泛用于这些射频前端的低中频接收机[2]中。本研究对多相滤波器的推动力来自于复函数的定量特性。我们的目标是建立一个六阶正交信号产生的数学模型，以验证无线通信系统中低中频接收机下的RC多相滤波器[3]。这些滤波器的传递函数是基于扩展的叠加原理简单推导得出的[4]。

在传统方法中，直接推导六阶多相网络的传递函数需要大量的计算。而采用所提出的叠加原理方法，则可以相对容易地进行推导，并利用MATLAB软件和SPICE仿真器进行仿真。

本文的结构安排如下。
第二部分介绍了多相位信号的相关概念以及正交信号产生网络的设计原理。第三部分分析了六阶正交信号产生的行为，第四部分展示了实验结果。第五部分得出了结论。

II. 多相位信号与设计原理

复信号可以根据相位顺序[5]分为正复信号和负复信号。通常情况下，复信号可以定义为 Scom{V1(t); V2(t)} ={1; ±j} V(t) ={1; ±j} Acos (ω0t+ϴ0)。其中，幅度为 A，确定的频率为 f0（或角频率 ω0= 2π f0），初始相位为 ϴ0。多相信号是复信号的一种差分形式。多相信号可定义为

$$
S_{poly}{V_1(t); V_2(t); V_3(t); V_4(t)} = {1; \pm j; \pm j^2; \pm j^3} A\cos(\omega_0 t + \theta_0)
\quad (1)
$$

利用低通和高通电路之间的互补性来设计无源正交信号生成网络，如图1所示。

)

)

(a) 二次发生器示意图 (b) 二次发生器电路

III. 六阶正交信号产生网络分析

在本节中，我们推导传递函数并分析六阶无源信号生成网络的行为，该网络首先由六个RC低通网络级联构成，其次为互补RC高通网络。假设该网络的输入源为正多相信号 Sp{V1(t);V2(t);V3(t);V4(t)}={1;(+j);(+j)2;(+j)3}V(t)。图2显示了一个六阶正RC多相网络。在节点 Va, Vb, Vc, Vd, Ve, Vout 处应用叠加原理，得到

$$
\begin{aligned}
&\left(1 + j\right)V_a + \frac{1}{Z_{C1}}\left(V_a - V_{out}\right) = \frac{1}{R_1}V_1 \
&\left(1 + j\right)V_b + \frac{1}{Z_{C2}}\left(V_b - V_a\right) = \frac{1}{R_2}V_2 \
&\left(1 + j\right)V_c + \frac{1}{Z_{C3}}\left(V_c - V_b\right) = \frac{1}{R_3}V_3 \
&\left(1 + j\right)V_d + \frac{1}{Z_{C4}}\left(V_d - V_c\right) = \frac{1}{R_4}V_4 \
&\left(1 + j\right)V_e + \frac{1}{Z_{C5}}\left(V_e - V_d\right) = \frac{1}{R_5}V_5 \
&\left(1 + j\right)V_{out} + \frac{1}{Z_{C6}}\left(V_{out} - V_e\right) = \frac{1}{R_6}V_6 \
\end{aligned}
\quad (2)
$$

通用传输函数和自环函数被重写为

$$
H(j\omega) = \frac{(1 + jb_1\omega)(1 + jb_2\omega)(1 + jb_3\omega)}{(1 + jb_4\omega)(1 + jb_5\omega)(1 + jb_6\omega)}
\quad (3)
$$

我们引入变量 ki （作为 i = 0:3）、li （作为 i = 0:5）、 mi （作为 i= 0:7）和 ni （作为 i = 0:9），以写出其简写形式。此处，给定变量的数值为

$$
\begin{aligned}
&b_1 = R_1C_1,\ b_2 = R_2C_2,\ b_3 = R_3C_3,\ b_4 = R_4C_4,\ b_5 = R_5C_5,\ b_6 = R_6C_6 \
&k_0 = b_1,\ k_1 = b_2,\ k_2 = b_3,\ k_3 = b_4 \
&l_0 = k_0C_1 + k_1C_2 + k_2C_3 + k_3C_4 \
&l_1 = k_0C_1b_1 + k_1C_2b_2 + k_2C_3b_3 + k_3C_4b_4 \
&l_2 = l_0 + l_1,\ \dots \
&m_0 = l_0C_5 + l_1C_6 + \dots \
&n_0 = m_0C_7 + m_1C_8 + \dots \
\end{aligned}
\quad (4)
$$

为了研究六阶正交信号生成网络在频域中的行为，计算了传递函数的幅值和相角

$$
\begin{aligned}
&\lim_{\omega \to 0^+} |H(j\omega)| = 1 \
&\max_1 = |H(j\omega)| \text{ at } f = 45\,\text{kHz} \
&\min = |H(j\omega)| \text{ at } f = 2\,\text{MHz} \
&\max_2 = |H(j\omega)| \text{ at } f = 100\,\text{MHz} \
&\lim_{\omega \to +\infty} |H(j\omega)| = 1 \
\end{aligned}
\quad (5)
$$

当无源器件的数值为 R1= 1 kΩ，C1= 318 pF， R2= 1 kΩ，C2= 199 pF，R3= 1 kΩ，C3=106 pF， R4= 1 kΩ，C4= 53.1 pF，R5= 1 kΩ，C5= 26.5 pF， R6 = 1 kΩ，C6 = 16.8 pF，在截止频率 f1 = 500 kHz，f2 = 800 kHz，以及 f3 = 1.5 MHz，f4 = 3 MHz，f5 = 6MHz，f6 = 9.5 MHz 时，幅值和相角在频域中被分析。

$$
\begin{aligned}
&\lim_{f \to 0^+} H(f) = 1 \
&Max_1 = 1.09\ \text{at}\ f = 45\,\text{kHz} \
&Min = 0.812\ \text{at}\ f = 2\,\text{MHz} \
&Max_2 = 1.09\ \text{at}\ f = 100\,\text{MHz} \
&\lim_{f \to +\infty} H(f) = 1 \
\end{aligned}
\quad (6)
$$

两个最大值位于 45 千赫、100 兆赫，一个最小值位于 2 兆赫，如图3所示。

IV. 测量结果

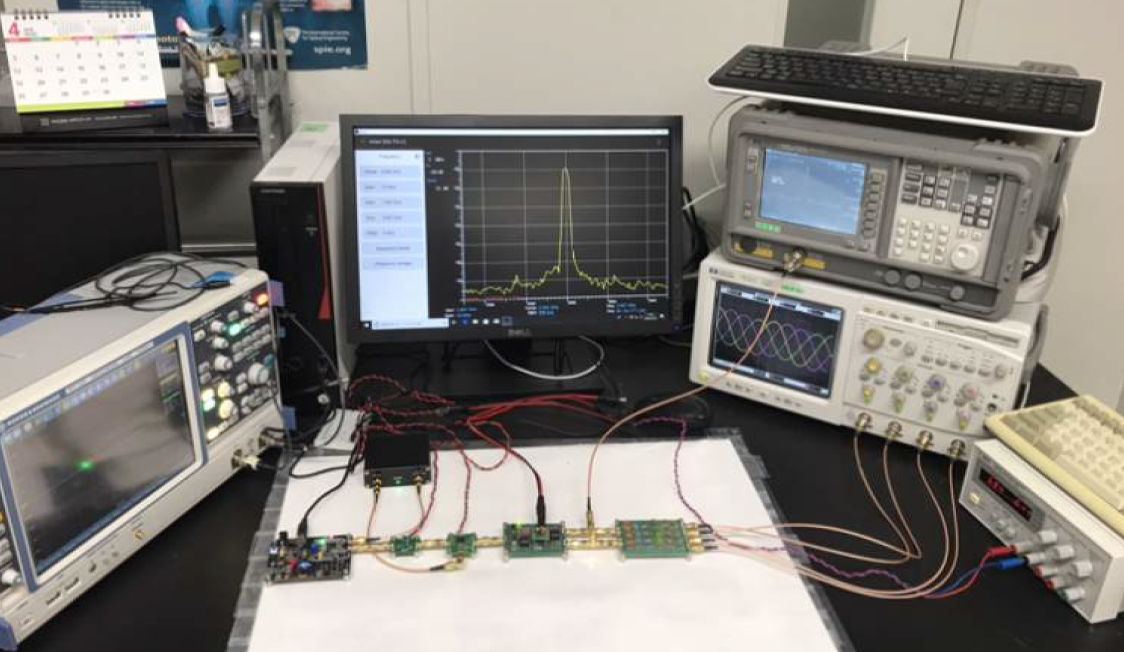
在实际设计中，寄生元件和选定的器件参数变化会影响电路行为。因此，传输函数测量为多相滤波电路的验证提供了多种可能性。图4显示了所提出的设计的原理图。使用网络分析仪、频谱分析仪、信号发生器、示波器和电源进行测量。所设计的低通滤波器的频率范围为50千赫至10兆赫。我们通过实验室电源为设计的电路提供6伏特电压，如图5所示。

图6显示了频域中传递函数的幅值和相位的频率响应。
在1千赫至10兆赫范围内，低于40千赫和高于2兆赫时出现了IQ失配。这些IQ失配是由寄生元件以及R、C元件的参数变化引起的。此外，测量设备的局限性和有源缓冲电路的特性也影响了测量结果。

V. CONCLUSION

本文介绍了六阶无源正交信号生成网络的设计考虑。所提出的网络的核心设计原理在于低通与高通网络之间的互补。
该网络的性能已在理论分析、理想仿真和实际测量中进行了讨论。在1千赫到10兆赫范围内，所提出的设计在实现中的IQ失配也在40千赫以下和2兆赫以上进行了测量。在未来工作中，我们将研究由寄生元件以及R、C元件的参数变化所引起的IQ失配。