A tree is an undirected connected graph without cycles.
Let's consider a rooted undirected tree with n vertices, numbered 1 through n. There are many ways to represent such a tree. One way is to create an array with n integers p1, p2, ..., pn, where pi denotes a parent of vertex i (here, for convenience a root is considered its own parent).
 For
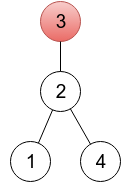
this rooted tree the array p is [2, 3, 3, 2].
For
this rooted tree the array p is [2, 3, 3, 2].Given a sequence p1, p2, ..., pn, one is able to restore a tree:
- There must be exactly one index r that pr = r. A vertex r is a root of the tree.
- For all other n - 1 vertices i, there is an edge between vertex i and vertex pi.
A sequence p1, p2, ..., pn is called valid if the described procedure generates some (any) rooted tree. For example, for n = 3 sequences(1,2,2), (2,3,1) and (2,1,3) are not valid.
You are given a sequence a1, a2, ..., an, not necessarily valid. Your task is to change the minimum number of elements, in order to get a valid sequence. Print the minimum number of changes and an example of a valid sequence after that number of changes. If there are many valid sequences achievable in the minimum number of changes, print any of them.
The first line of the input contains an integer n (2 ≤ n ≤ 200 000) — the number of vertices in the tree.
The second line contains n integers a1, a2, ..., an (1 ≤ ai ≤ n).
In the first line print the minimum number of elements to change, in order to get a valid sequence.
In the second line, print any valid sequence possible to get from (a1, a2, ..., an) in the minimum number of changes. If there are many such sequences, any of them will be accepted.
4 2 3 3 4
1 2 3 4 4
5 3 2 2 5 3
0 3 2 2 5 3
8 2 3 5 4 1 6 6 7
2 2 3 7 8 1 6 6 7
In the first sample, it's enough to change one element. In the provided output, a sequence represents a tree rooted in a vertex 4(because p4 = 4), which you can see on the left drawing below. One of other correct solutions would be a sequence 2 3 3 2, representing a tree rooted in vertex 3 (right drawing below). On both drawings, roots are painted red.

In the second sample, the given sequence is already valid.
#include<stdio.h>
#include<iostream>
#include<string.h>
#include<string>
#include<ctype.h>
#include<math.h>
#include<set>
#include<map>
#include<vector>
#include<queue>
#include<bitset>
#include<algorithm>
#include<time.h>
using namespace std;
void fre() { freopen("c://test//input.in", "r", stdin); freopen("c://test//output.out", "w", stdout); }
#define MS(x,y) memset(x,y,sizeof(x))
#define MC(x,y) memcpy(x,y,sizeof(x))
#define MP(x,y) make_pair(x,y)
#define ls o<<1
#define rs o<<1|1
typedef long long LL;
typedef unsigned long long UL;
typedef unsigned int UI;
template <class T1, class T2>inline void gmax(T1 &a, T2 b) { if (b>a)a = b; }
template <class T1, class T2>inline void gmin(T1 &a, T2 b) { if (b<a)a = b; }
const int N = 2e5+10, M = 0, Z = 1e9 + 7, ms63 = 0x3f3f3f3f;
int n;
int fa[N];
int vis[N];
vector<int>root, cir;
int tim;
void dfs(int x)
{
if (vis[x] == tim)
{
cir.push_back(x);
return;
}
if (vis[x])return;
vis[x] = tim;
dfs(fa[x]);
}
int main()
{
while (~scanf("%d", &n))
{
for (int i = 1; i <= n; ++i)
{
scanf("%d", &fa[i]);
vis[i] = 0;
}
root.clear(); cir.clear();
for (int i = 1; i <= n; ++i)
{
if (fa[i] == i)
{
root.push_back(i);
vis[i] = -1;
}
}
tim = 0;
for (int i = 1; i <= n; ++i)if(!vis[i])
{
++tim;
dfs(i);
}
int ans = 0;
int rt;
if (root.size())rt = root[0];
else rt = cir[0];
for (int i = 0; i < root.size(); ++i)
{
int x = root[i];
if (fa[x] != rt)
{
fa[x] = rt;
++ans;
}
}
for (int i = 0; i < cir.size(); ++i)
{
int x = cir[i];
if (fa[x] != rt)
{
fa[x] = rt;
++ans;
}
}
printf("%d\n", ans);
for (int i = 1; i <= n; ++i)printf("%d ", fa[i]);
puts("");
}
return 0;
}
/*
【trick&&吐槽】
这题做的时候没笔纸,瞎想想错了,
然后竟然做了好久才AC,真是太傻逼了。
【题意】
n(2e5)个点的图,每个点一条出边。
让你修改尽可能少的点的出度,使得这棵树变为反向有根树
(也就是所有点都可以沿着出边走,最终汇聚到根节点)
【类型】
环套树 贪心 脑洞
【分析】
首先,我们应该有大体的图形态构想。
每个点有且只有一条出边,我们形成的会是一个环套树结构
(树的根为一个点或者为一个环)
我们可以把树根为一个点的存到root中
把树根为环的通过每个点只走一遍的暴力dfs(在环套树的任一点做dfs,最终一定可以找到环并停留在环上一点)
找到环上任一点,然后把这点存到cir中。
我们如果没有root,选择cir[0]为rt(根)
然后把其他的root和cir上点都连到root上就可以AC啦
【时间复杂度&&优化】
O(n)
*/






 解决一道算法题目,关于调整不完整的树结构使之成为有效的有根树,介绍了解题思路及实现过程。
解决一道算法题目,关于调整不完整的树结构使之成为有效的有根树,介绍了解题思路及实现过程。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








