基于深度置信网络的聚合物熔融指数软测量

工业聚合过程中聚合物熔融指数软测量传感器的开发 工业聚合过程使用 深度置信网络

1 引言

过去几十年中，在过程控制研究领域，针对软传感器的研究已开展了大量工作。该技术在工业化学过程中得到了广泛应用。软传感器是用于估计工业过程中某些重要产品质量变量的有效技术，这些变量难以被直接有效测量。在过程控制领域，硬件仪器存在的问题（例如不可用或高成本）阻碍了产品质量控制。为克服这些问题，可基于从实际工业过程中获取的操作数据建立经验模型。借助此类模型，难以测量的质量变量可以从易于测量的过程变量中进行估计[1]。这种基于历史过程数据的建模技术近年来在化学过程中日益流行。这类数据驱动模型可有效用于降低工业过程中的生产成本并提高效率。

基于多元统计技术的过程建模方面已完成了大量成功的研究在上个世纪。1901年，皮尔逊[2]提出了主成分分析法（PCA）。该方法在20世纪30年代由哈罗德·霍特林进一步发展[3, 4]。基于PCA，主成分回归（PCR）和偏最小二乘法（PLS）作为解决输入变量间共线性问题的有用建模方法应运而生[2]。可通过使用主成分作为预测变量，基于PCR开发数据驱动的软传感器。作为PCR的改进，PLS回归能够同时对过程数据和质量数据进行建模[5]。Wold 等人[6]首次引入了PLS，随后Wold对其进行了进一步发展。在过程建模中，有许多基于PLS技术的应用。PLS和PCR的一个局限性在于它们均为线性技术，在应用于非线性过程建模时效果不佳。

随着机器学习的发展，过去几年中已报道了许多关于基于机器学习技术开发软传感器的研究。有许多基于机器学习的成功的过程建模技术，例如支持向量机（SVM）和人工神经网络（ANN）。麦卡洛克和皮茨[7]在20世纪40年代提出了最初的神经网络。20年后，随着计算机能力的大幅提升，神经网络成为一个热门的研究课题。反向传播算法由韦博斯[8]于1975年应用于人工神经网络（ANN）。人工神经网络的优点在于它们可以用来逼近任何非线性函数。人工神经网络在质量数据的估计和预测方面表现出色。反向传播算法能够处理异或问题。在反向传播训练算法中，神经元之间的权重被修改，以将误差从输出层反向传播上去[8]。然而，传统的ANN存在局部最优问题且泛化能力不足。支持向量机即使在训练数据较少的情况下也能达到可达最优。当将SVM应用于建模数据量较大的过程时，计算压力会增加。2006年，欣顿等人[9]首次提出了深度学习。深度置信网络（DBN）是基于深度学习的最著名的数据驱动建模技术之一。它在对高度非线性过程进行建模时表现出强大的泛化能力。该模型采用深层结构建立。深度学习在语音识别和图像分类等领域有广泛应用[10]。DBN训练过程包含两个训练阶段：先进行无监督训练，然后进行监督训练。在监督训练之前，DBN会从非线性过程输入数据中捕获更多信息，以实现对质量数据更准确的预测或估计。它在许多其他应用中也表现出显著性能[11]。

本研究利用深度置信网络（DBN）建立了聚合物熔融指数（MI）的软传感器，并将其应用于工业聚丙烯（PP）聚合过程。通过使用深度学习技术，大量没有预先存在的标签的工业过程数据样本也可以在无监督训练阶段被DBN模型所利用。然而，这些输入数据对于仅采用监督训练的传统前馈神经网络而言是无用的。这些过程数据样本有助于DBN模型在理想区域内调整权重。在无监督训练过程中捕获了来自过程数据的信息。本文结果表明，DBN模型对MI给出了非常准确的估计值。

本文的其余部分组织如下。第2节介绍了人工神经网络。第3节介绍了深度置信网络模型以及受限玻尔兹曼机（RBMs）和反向传播的主要原理。第4节介绍了一个工业聚丙烯聚合过程的案例研究。第5节讨论了深度置信网络模型架构的选择，并给出了聚合物熔融指数的估计结果。第6节总结了本文的结论。

2 人工神经网络

前馈神经网络是最著名的机器学习技术之一，可用于解决预测、分类和模式识别中的许多问题。过去几十年中已报道了大量关于人工神经网络的研究。在最初的形式中，它是一种简单的由麦卡洛克和皮茨发明的感知器，该模型计算输入变量的加权和，然后将其传递给激活函数。图 1 展示了一个简单感知器结构。

从图 1 可以看出，$x_i, i= 1, 2, \cdots, n$ 是输入变量，而 $w_j, j= 1, 2, \cdots, n$ 是这些输入变量对应的权重。麦卡洛克和皮茨[7]使用阈值函数作为激活函数。他们证明，如果适当选择权重，简单感知器可以执行通用计算。然而，许多复杂系统无法用此方法表示[14]。还可以使用许多其他激活函数，例如海维赛德阶跃函数、Sigmoid函数和高斯函数。这些激活函数在人工神经网络研究中有时也被称为传递函数。最流行的激活函数是Sigmoid函数。

Sigmoid函数的特点是呈“S”形曲线，如图 2 所示。

Sigmoid函数将输入值映射到0到1的范围内。在图 2 中，当x趋近于+ ∞时，输出值趋近于1；而当x趋近于– ∞时，输出值趋近于0。它具有适当的渐近特性。Sigmoid函数由公式(1)给出：

$$
S(x)= \frac{1}{1+ e^{- \beta x}} \tag{1}
$$

其中x表示加权输入值的总和，β是斜率参数。

人工神经网络的结构可以被视为神经元被组织成相互连接的层，相邻层之间的神经元具有加权连接。基本上，前馈神经网络和循环网络是人工神经网络的两种主要类型。前馈网络没有来自网络输出的反馈连接。循环神经网络是一种具有反馈连接的神经网络。在本研究中，前馈网络也被用于聚丙烯聚合过程中的软传感器开发，以与深度置信网络进行比较。

多层感知器是最经典的前馈网络类型，能够处理比简单感知器更复杂的问题。相邻层的神经元单向连接，没有反馈回路。一个多层感知器模型至少包含三层，通常由输入层、隐藏层和输出层构成。神经网络输入与输出变量之间的关系可以通过监督训练过程学习，并以训练好的网络权重形式存储。具有两个隐藏层的多层感知器结构如图 3 所示。

输入层中的每个单元都是网络的输入。隐藏层或输出层中某个单元的输出是通过将前一层加权输出的总和传递给激活函数来计算的，公式如下：

$$
O_j = f\left( \sum_{i=1}^{n} w_{ij} I_i + b_j \right) \tag{2}
$$

其中，$O_j$ 是某一层中单元$j$的输出值，$w_{ij}$ 是该单元与前一层第$i$个单元之间的权重，$I_i$ 是该单元的第$i$个输入（即前一层中第$i$个单元的输出值），$b_j$ 是偏置，$f$ 是激活函数。在网络训练过程中，权重和偏置通常被初始化为介于– 0.1 和 0.1 之间的随机值。通过使用训练算法调整网络权重，以最小化网络输出与目标标签之间的误差项。训练完成后，系统输入变量与输出变量之间的关系可由训练好的模型表示神经网络。训练多层前馈神经网络的过程是监督训练。最常用的监督训练算法是反向传播算法。多层前馈神经网络具有建模非线性过程的能力。然而，聚合过程具有高度非线性。通常使用的多层神经网络结构为浅层结构。当前馈神经网络在使用反向传播进行超过三层的训练时，模型常常存在泛化能力差的问题。这种建模技术无法满足估计准确性的需求。为了实现对混合指数（MI）更准确的估计，本研究建立了DBN模型。DBN具有深层结构和更强的泛化能力。

3 深度置信网络

3.1 深度置信网络结构

传统神经网络的局限性在于它们通常具有浅层结构。传统的神经网络模型中通常不超过三层。由于这一限制，当应用于高度非线性的工业过程时，浅层结构的神经网络可能无法达到令人满意的估计性能。实际工业过程通常具有高度非线性。前馈神经网络的浅层架构可能导致表示能力不足[15, 16]。为了逼近过程的各个区域，模型需要在隐含层中增加更多的隐层神经元。最近的研究表明，具有深层结构的网络能够获得可靠结果[15]。深度置信网络（DBN）已成功应用于许多研究领域，如分类和识别[17]。在DBN模型中，多个受限玻尔兹曼机（RBMs）可以堆叠并组合成一个学习网络。DBN基于深度学习技术构建了深层结构。图 4 展示了DBN基本结构。

图. 4所示的DBN具有五层，包括一个输入层、一个输出层和三层隐含层。在图 4 中，W是网络的权重，b和c是网络的偏置。可以认为DBN是堆叠RBM的组合。DBN的每个隐层被视为一个单独的玻尔兹曼机。与传统的玻尔兹曼机相比，DBN隐层中的神经元彼此之间不连接，但网络中的层之间具有对称连接。隐层中的单位是二值单元，可见输入层单元是高斯单元。训练的第一阶段是无监督训练，该过程使用操作数据来训练DBN模型，无需涉及任何目标变量。无监督训练有助于DBN比前馈神经网络挖掘出更多的相关性。权重被调整在监督训练阶段之前进入期望区域。无监督训练后，深度置信网络在监督训练阶段通过反向传播算法进行微调。

3.2 受限玻尔兹曼机

20世纪80年代，斯莫伦斯基[18]提出了受限玻尔兹曼机。欣顿等人[10]通过将受限玻尔兹曼机堆叠为深度置信网络的层来构建DBN。DBN包含堆叠的受限玻尔兹曼机，如图 4 所示。为了理解玻尔兹曼机的基本原理，首先需要介绍可见单元和隐单元之间的概率函数。公式(3)展示了该概率函数

$$
P(v,h)= \frac{\exp{-Energy(v,h)}}{Z} \tag{3}
$$

其中，Z 表示归一化因子，v 表示可见层的向量，h 表示隐藏层的向量。当能量函数减小时，概率 $P(v, h)$ 增大。在玻尔兹曼机中，能量函数由下式给出

$$
Energy(v,h)= -b^T v - c^T h - h^T Wv \tag{4}
$$

其中，W、b 和 c 是该函数的参数。需要注意的是，向量 v 和向量 h 均为二值变量。二值受限玻尔兹曼机被用作深度置信网络模型中的隐含层。然而，它们无法处理连续变量。为了解决这一问题，(4) 可以扩展为高斯受限玻尔兹曼机的能量函数：

$$
Energy(v,h)=\sum_{i} \frac{(v_i - a_i)^2}{2\sigma^2_i} - c^T h - h^T Wv \tag{5}
$$

其中$a_i$ 是高斯分布的均值， $\sigma_i$ 是输入神经元高斯分布的标准差。在实际应用中，输入数据的样本通常被归一化为零均值和单位方差应用。因此，(5) 可以更改为

$$
Energy(v,h)= \frac{1}{2} v^T v - b^T v - c^T h - h^T Wv. \tag{6}
$$

辛顿[19]还描述了其他形式的玻尔兹曼机，但本文中的深度置信网络仅使用高斯受限玻尔兹曼机和二值受限玻尔兹曼机。

3.3 受限玻尔兹曼机学习算法

训练受限玻尔兹曼机的目标是最大化概率P(v)，这可以通过最小化能量函数来实现。根据吉布斯采样，隐层h只能从可见层的可见点v中进行采样。基于先前的研究，可见点 v处的梯度可以表示为

$$
\frac{\partial \log P(v)}{\partial \theta} = \frac{\partial \log \sum_h P(v,h)}{\partial \theta} = \frac{\sum_h e^{-Energy(v,h)}(\partial[-Energy(v,h)] / \partial \theta)}{\sum_h e^{-Energy(v,h)}} - \frac{\sum_{\tilde{v}} \sum_h e^{-Energy(\tilde{v},h)}(\partial[-Energy(\tilde{v},h)] / \partial \theta)}{\sum_{\tilde{v}} \sum_h e^{-Energy(\tilde{v},h)}} = \sum_h P(h|v) \frac{\partial [-Energy(v,h)]}{\partial \theta} - \sum_{\tilde{v}} \sum_h P(\tilde{v},h) \frac{\partial [-Energy(\tilde{v},h)]}{\partial \theta} \tag{7}
$$

其中$\theta={W, b, c}$是网络参数的向量。(7)中的正项计算较为简单，因为向量v已知。而(7)中负项的计算则变得难以处理。对比散度是一种有效的方法，可用于克服计算负项二阶近似所带来的困难，并提供了一种有效的解决方案[20, 21]。训练受限玻尔兹曼机的过程始于在可见单元上使用训练向量，然后通过吉布斯采样从生成隐单元，并从更新可见单元，这一过程称为马尔可夫链。经过无限次迭代的吉布斯采样后，可见单元v采样即可获得满意的结果，且学习算法表现良好。

3.4 通过反向传播进行监督训练

反向传播是最常用的监督有监督训练方法用于训练神经网络。在无监督训练阶段之后，反向传播算法将在监督训练阶段对整个网络进行微调。计算网络输出与对应标签之间的误差，并将误差反向传播到前一层。公式(8)显示了误差项

$$
Err_j= O_j(1 - O_j)(T_j - O_j) \tag{8}
$$

其中$O_j$表示网络对一个训练样本的输出，$T_j$表示第j个输出神经元对应的目标值。隐含层误差项的表达式为

$$
Err_j= O_j(1 - O_j)\sum_k Err_k w_{jk} \tag{9}
$$

其中，$w_{jk}$ 是连接输出层和最后一个隐藏层的权重向量， $Err_k$ 是输出层的误差项。在训练过程中，权重更新从输出层传递到输入层。权重更新的公式如下所示

$$
w_{ij}= w_{ij}+ \eta Err_j O_i \tag{10}
$$

$$
c_j= c_j+ \eta Err_j \tag{11}
$$

其中 η是训练过程的学习率，$w_{ij}$和$c_j$分别是权重和偏置的向量。学习率需要适当选择，过大的学习率可能错过最小值，而过小的学习率通常导致训练速度缓慢。

如前所述，深度置信网络的训练包含一个无监督训练阶段和一个监督训练阶段。在无监督训练过程中，初始权重被调整到适当区域。随后，在监督训练阶段通过反向传播对整个网络进行微调，以获得精确的建模结果。在无监督训练期间从输入变量中提取的丰富潜在信息更具可解释性。这种半监督方法提高了深层结构模型的鲁棒性和泛化能力。

4 聚丙烯聚合过程

先进监控、控制和优化技术在现代工业化学过程中至关重要，可克服高成本问题并提高生产效率[22]。本文中，采用深度置信网络（DBN）为中国某聚丙烯生产装置开发软传感器。该装置如图 5 所示，采用两个连续搅拌釜反应器（CSTR）和两个流化床反应器（FBR）生产聚丙烯。丙烯、氢和催化剂被送入反应器。反应用于生长的聚合物颗粒的原料是进料到反应器中的这些气体和液体。它们也是传热介质的提供者。聚合物的熔体指数是关键的聚合物质量变量，应密切监测和控制。聚丙烯的熔体指数受催化剂、反应器温度和反应物料浓度等多种因素影响。例如，氢气可以提高聚丙烯的聚合速率，主要增加丙烯的初始聚合速率[23]。氢气浓度调节聚丙烯的分子量。氢气还可以延缓催化剂的失活速率。由于在此过程中测量聚合物熔体指数存在困难，因此需要找出熔体指数与一些在过程中易于测量的过程变量之间的关系。可通过软传感器获得对熔体指数的推断估计。由于该工业过程非常复杂，难以建立将聚合物熔体指数与易测过程变量关联起来的机理模型。因此，在开发该过程的软传感器时，需要采用非线性数据驱动模型。

聚丙烯牌号与一些关键变量相关，例如反应物组成、反应器温度和催化剂特性。D201的原料为丙烯、氢和催化剂。共聚单体被加入到D204中。在一个时间段内生产了多种聚合物牌号。该应用可获取覆盖此时间段的工业过程运行数据。在此过程中，每两小时记录一次聚合物熔体指数，每半小时记录一次过程样本。事实上，熔体指数仅与少数几个过程变量高度相关。根据张等人的研究[24], ，D204反应器中聚合物的熔体指数与D201和D202反应器中的氢浓度之间存在强相关性。D201反应器中聚合物的熔体指数与氢浓度和进料速率高度相关201[24]。D201和D202中的氢浓度、氢气进料速率以及D201和D204反应器中聚丙烯的熔体指数分别如图 6– 8 所示。由于工业保密性，这些变量的单位未公开。

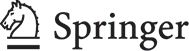
从图 8 可以看出，熔体指数数据覆盖了相当广泛的范围。因此，这些数据适用于进行开发数据驱动模型。软传感器应从有限的过程数据和质量数据中提取信息，以准确估计混合指数。从图 6–8所示的趋势可以看出，混合指数与氢气进料速率和浓度高度相关。

基于互相关分析[24]可以找到工业过程的时间延迟。用于混合指数推断估计的数据驱动模型可以表示为

$$
MI_1(t)= f_1[H_1(t), H_1(t - 1), H_1(t - 2), F(t - 9), F(t - 10), F(t - 11)] \tag{12}
$$

$$
MI_2(t)= f_2[H_1(t - 7), H_1(t - 8), H_1(t - 9), H_2(t - 6), H_2(t - 7), H_2(t - 8)] \tag{13}
$$

其中$MI_1$和$MI_2$分别为D201和D204中的混合指数，$H_1$和$H_2$分别为D201和D202中氢的浓度，F为进入D201的氢气进料速率。

原始过程数据集包含1534个过程操作数据样本和383个质量数据（混合指数）样本，可用于建立数据驱动的DBN模型。这表明过程变量样本的数量大于质量变量样本的数量。其中仅有383个过程变量样本具有对应的质量变量。然而，其余的过程变量样本可以在无监督训练阶段被DBN利用。通过这种方式，DBN能够从过程数据中捕获大量有价值的信息，从而提高对混合指数的估计精度。

监督训练阶段的数据集被划分为训练数据集、测试数据集和未见验证数据集。用于估计混合指数 1 的数据集划分如表1所示。用于估计混合指数 2 的数据集划分如表2所示。

模型结构的选择可以通过训练数据集和测试数据集利用交叉验证来确定。未见验证数据对于测试最终开发的深度置信网络模型的性能。

D201和(b) D202中的浓度)

D201 和 (b) D204 中的熔体指数)

由表1和2可知，选择了277个训练和测试变量样本，通过反向传播对深度置信网络进行微调以用于混合指数1 ，而深度置信网络仅使用268个训练和测试变量样本来在监督训练阶段对深度置信网络进行微调以用于混合指数2。在DBN模型的无监督训练阶段，只需要输入数据，而不需要目标值。那些没有相应输出数据的输入数据样本被称为“无标签”过程数据。因此，在DBN模型的无监督训练阶段，即使没有相应熔体指数数据的过程变量样本也可以被利用。然而，这些 “无标签”的过程变量无法被其他传统神经网络用于产品质量的推断估计。为了进行比较，也开发了传统神经网络模型。

表 1 数据集的划分 用于估计混合指数1

数据集	百分比	样本数量
训练数据	50%	192
测试数据	22%	85
未见验证数据	28%	106

表 2 数据集的划分 用于估计混合指数2

数据集	百分比	样本数量
训练数据	52%	200
测试数据	18%	68
未见验证数据	30%	115
## 5 结果与讨论

首先需要确定模型结构。在本研究中，开发并比较了 25个不同架构的DBN模型。在测试数据集上表现最佳的模型被视为具有适当的结构。这些DBN模型包含一个可见层（输入层）、一个额外的顶层（输出层）以及两个隐含层。无监督训练阶段的学习率为0.01，监督训练阶段的学习率为0.001。 25个深度置信网络模型的结构如表3所示。图 9和 10分别展示了这25个DBN模型在训练数据集和测试数据集上估计混合指数1时的平方误差和(SSE)。

从图9和图10可以看出，第7个DBN模型在测试数据集上具有最佳的泛化性能。第6个DBN模型在测试数据集上的误差值排名第二低。第12到第25个DBN模型的训练误差低于第7个DBN模型，但这些模型的测试误差大于第7个DBN模型。因此，第12到第25个DBN模型可能遭受了过拟合，其结构不适合被选用。根据图 9 和 10的结果，第一隐含层中的神经元数量可视为5。由表 3可知，这25个深度置信网络模型在第一和第二隐含层中的神经元数量相近。本研究的第一步是确认第7个DBN在这 25个DBN模型中表现最佳。为了避免未包含在表3中的某些 DBN模型可能表现出更优性能的情况，第二步是进一步研究第二隐含层中神经元的数量。构建了另外9个第二隐含层神经元数量从2到10的DBN模型。这些DBN模型在训练和测试数据上的误差项值如表4所示。

表 3 深度置信网络 模型 具有 不同 结构

No.	第一隐藏层中的神经元	第二隐藏层中的神经元	No.	第一隐藏层中的神经元	第二隐藏层中的神经元
1	2	1	14	8	7
2	2	2	15	9	9
3	3	3	16	9	8
4	3	2	17	10	10
5	4	4	18	10	9
6	4	3	19	11	11
7	5	5	20	11	10
8	5	4	21	12	12
9	6	6	22	12	11
10	6	5	23	13	13
11	7	7	24	13	12
12	7	6	25	14	13
13	8	8

表 4 误差 的 深度置信网络 模型 与 不同 结构 用于估计 混合指数1

No.	第一隐藏层中的神经元	第二隐藏层中的神经元	SSE (训练)	SSE (测试)
1	5	2	0.7562	0.5819
2	5	3	0.8204	0.6193
3	5	4	0.7824	0.5945
4	5	5	0.7696	0.5118
5	5	6	0.8206	0.5773
6	5	7	0.7271	0.5742
7	5	8	0.6723	0.5859
8	5	9	0.7628	0.6071
9	5	10	0.7372	0.6322

从表4可以看出，第7个DBN的训练误差最小，但其测试误差并非最小。第6到第9个DBN的测试误差呈上升趋势，因此第6到第9个DBN模型在测试数据上的估计结果出现了过拟合。第4个DBN（即表3中的第7个DBN模型）在所有 DBN模型中具有最低的测试误差。这表明第4个DBN模型的性能优于其他模型，应采用该模型的结构。

为了证明在无监督训练阶段使用那些没有对应目标值的输入数据样本作为额外训练数据的优势，还开发了一个仅在无监督训练阶段使用具有预先存在的标签的输入数据样本进行训练的DBN模型。这在表5中由深度置信网络编号1表示，其中深度置信网络编号2是通过使用没有对应MI样本的“无标签”过程数据构建的。表5中的深度置信网络编号2实际上是表5中的第4个DBN模型。表4中的两个DBN模型具有相同的结构。从表5可以看出，第一个 DBN模型在训练、测试和验证数据集上的SSE值均大于第二个DBN模型。因此，DBN可以从“无标签”数据中提取更多特征。深度置信网络编号2的性能优于深度置信网络编号 1。

表 5 误差 的 深度置信网络 模型 用于 估计 混合指数1 不同输入数据的 输入 数据

深度置信网络 编号	SSE（训练）	SSE（测试）	SSE（验证）
1	1.6203	0.8905	0.7024
2	0.7696	0.5118	0.6851

为了进行比较，还建立了七个传统的单隐层前馈神经网络模型。这些具有不同结构的传统前馈神经网络在训练和测试数据上的误差平方和值如表6所示。从表6可以看出，第4 个神经网络在估计MI1的测试数据上具有最低的SSE，在估计MI2的测试数据集上，第3个神经网络具有最低的 SSE。

未见验证数据上混合指数1 的深度置信网络与传统前馈神经网络的估计值如图 11所示。在图 11中，实线、虚线和点划线分别表示混合指数1 ,的实际值、深度置信网络的估计值以及传统前馈神经网络的估计值。从图 11可以看出，深度置信网络模型的估计值通常比前馈神经网络的估计值更接近相应的混合指数 1 实际值。深度置信网络和神经网络的误差平方和值列于表7中。由表7可见，深度置信网络在训练数据集上的误差平方和大于神经网络。然而，深度置信网络在测试和未见验证数据集的误差远小于神经网络。深度置信网络对混合指数1的推断估计证明了其强大的泛化能力，性能优于前馈神经网络。在无监督训练阶段，深度置信网络从过程数据中提取了丰富的潜在信息。总体而言，深度置信网络模型对混合指数1的估计值更加准确。

图 12 比较了深度置信网络和传统前馈神经网络在未见验证数据上对混合指数2的估计值。在图 12中，实线、虚线和点划线分别表示混合指数2,的实际值、深度置信网络的估计值以及传统前馈神经网络的估计值。从图 12可以看出，当混合指数值较高时，两个模型的表现相似；但当混合指数值较低时，深度置信网络模型提供了更好的估计。表8 显示了混合指数估计中的误差平方和值。深度置信网络在训练数据上的误差平方和大于神经网络，但在测试和未见验证数据上的误差平方和集合的规模远小于神经网络模型。图 12 和 表8 中的结果表明，深度置信网络对混合指数2的估计值比传统的前馈神经网络更可靠且更准确。

表 6 误差 的 神经 网络 与 不同 结构

No.	神经元在隐藏层	MI1 SSE (训练)	MI1 SSE (测试)	MI2 SSE (训练)	MI2 SSE (测试)
1	2	1.3256	0.7446	1.6025	0.6855
2	3	0.7949	0.8221	1.5185	0.7374
3	4	0.7924	0.6527	1.5035	0.6564
4	5	0.7675	0.6323	1.3650	0.6883
5	6	0.6347	0.6532	1.1009	0.8214
6	7	0.5124	1.1054	0.7844	0.8305
7	8	0.4201	0.8895	0.5108	1.6024

表 7 误差平方和 of estimating 混合指数1

模型	SSE（训练）	SSE（测试）	SSE（验证）
神经网络	0.7675	0.6323	0.8243
DBN	0.7696	0.5118	0.6851

表 8 误差平方和 的 估计 混合指数2

模型	SSE（训练）	SSE（测试）	SSE（验证）
神经网络	1.5035	0.6564	0.9915
DBN	1.5170	0.4342	0.8560

6 结论

本文研究了用于工业聚合过程中聚合物熔融指数在线推断估计的深度置信网络模型。深度置信网络可以构建深层结构，从而提取过程变量中的丰富潜在信息。传统神经网络模型无法利用的“无标签”过程数据，可在深度置信网络的无监督训练阶段加以使用。本文表明，采用该方法可提高聚合物熔体指数推断估计的准确性。文中对深度置信网络结构的选择进行了研究，选定了适用于MI1和MI2估计的适当 DBN结构。与传统的前馈神经网络相比，深度置信网络表现出更优的性能。研究表明，深度置信网络非常适用于开发用于聚合物熔融指数推断估计的非线性数据驱动模型。所提出的深度置信网络模型未来还可拓展用于构建多步超前预测模型。深度置信网络的网络结构可进一步优化以提升其鲁棒性。