原始视频:
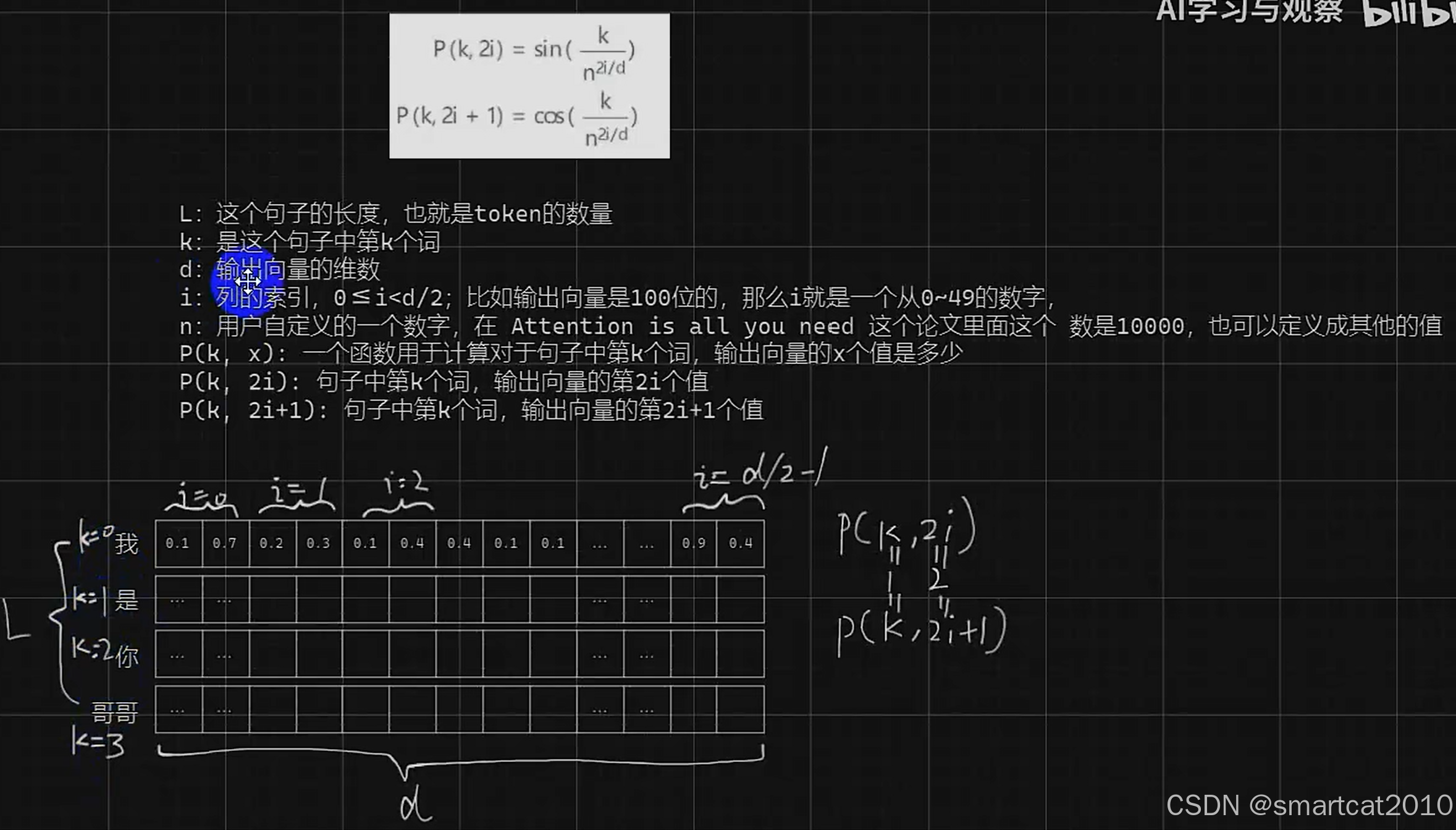
对某个维度而言,分母是固定的,值在[-1, 1]之间,随着token位置k,做周期性变化。
对同一个token而言,分子k是固定的,分母从1增大到n(10000),即周期从6.28逐渐增长到62800.
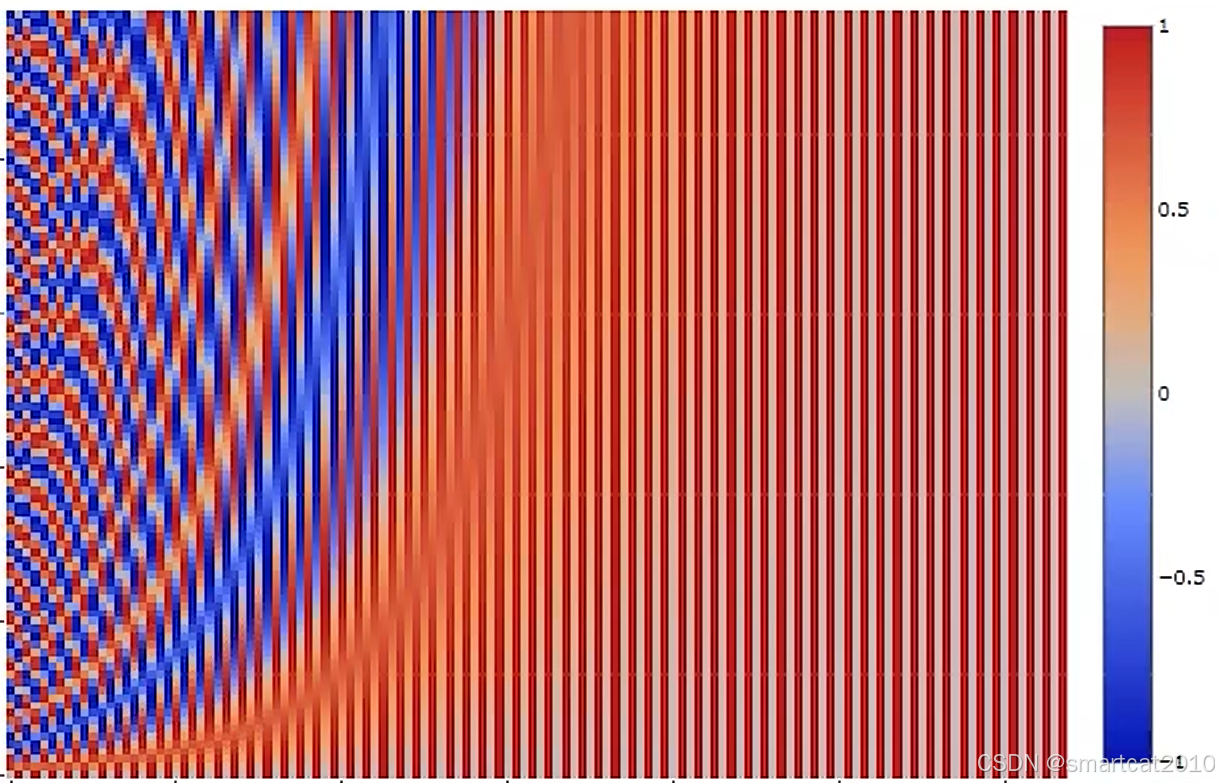
横轴是维度i,纵轴是token位置k。
相邻条纹,体现sin和cos的大差异。
截取竖着的一条(某维度),i小时,因为周期小(6.28),所以值随着k而变化剧烈;
截取竖着的一条(某维度),i大时,因为周期大(62800),所以值随着k而变化非常小;
截取横着的一条(某token),i小时,周期的变化大,值波动大;i大时,周期的变化小,值波动小;
Rotary Positional Embedding(RoPE)
用在LLama attention计算,q和k的向量乘法中。
给Query向量和Key向量,引入位置信息(旋转一定角度,该角度正比于该token在句子中的位置),q和k的点乘就变成了q旋转后的向量和k旋转后的向量进行点乘,等价于q旋转相对角度后和k进行点乘。
-------------
[1, 0]向量乘以旋转矩阵:(可以视为positional embedding的类似)
任意2维单位向量,乘以旋转矩阵:
-------------
扩展到多维:
m是token在句子中的位置。i是当前特征在第几维度,d是特征总维度。
前面的特征维度,f较大,mf这个旋转角度随位置m的变化而变化大;
后面的特征维度,f较小,mf这个旋转角度随位置m的变化而变化小;
-------------
特性1:连续旋转2个角度,等于一次旋转2个角度之和。
特性2:旋转矩阵的转置,等于旋转负角度。
从特性1和特性2,可推导2个向量的点乘:
q向量旋转了m角度,k向量旋转了n角度,二者的点乘,等于q旋转m-n角度再点乘k。
m只和q的token位置有关。n只和k的token位置有关。
因此,点乘结果,只和两个向量各自token的相对位置有关,和各自绝对位置无关了。
实际计算中,可以将R实现计算完缓存好,q乘以R(m),k乘以R(n),二者再点乘。




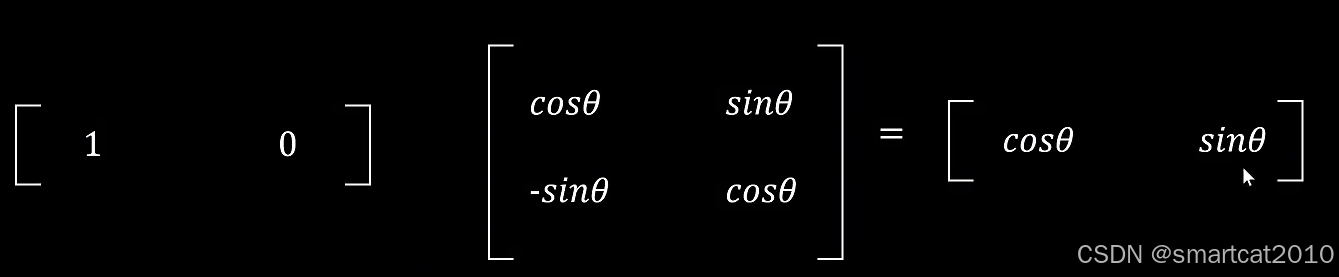


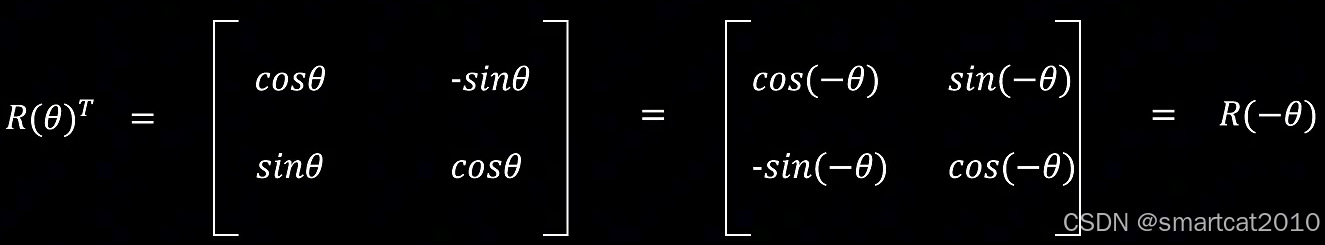
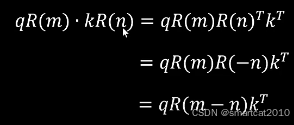
















 1582
1582

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








