leetcode hot100 之不同的二叉搜索树

最新推荐文章于 2025-03-17 21:37:11 发布

原创最新推荐文章于 2025-03-17 21:37:11 发布 · 270 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#leetcode #算法 #动态规划

LeetCode 专栏收录该内容

143 篇文章

订阅专栏

该博客介绍了如何使用动态规划解决LeetCode上的'不同二叉搜索树'问题。通过建立转移方程G(n) = ∑i=1nF(i,n)，其中F(i,n)表示以i为根节点的二叉搜索树的数量，逐步计算得出结果。此外，还提到G(n)与卡塔兰数的关系，并提供了C++实现的代码示例。

题目

给定一个整数 n，求恰由 n 个节点且节点值由 1 ~ n 构成的二叉搜索树有多少种。
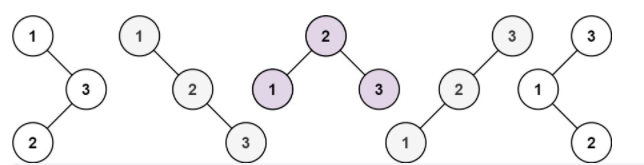
在这里插入图片描述

输入：n = 3
输出：5

原题链接：https://leetcode-cn.com/problems/unique-binary-search-trees/

思路

首先说明一下二叉搜索树的定义：左子树所有节点小于根节点，右子树所有节点大于根节点。

动态规划法。找到转移方程是关键。

假定 G(n) 表示：节点数为 n 的二叉搜索树有多少种。
F(i, n) 表示：以 i 为根节点，节点数为 n 的二叉搜索树有多少种。
那么
$\sum^n_{i=1}F(i, n)$
同时，边界情况，G(0) = 1， G(1) = 1

那么我们来看看 F(i, n) 如何求解。
在给定根节点 i 后，左子树是 [1, 2, …, i - 1] 构成的二叉搜索树；右子树是 [i + 1, …, n] 构成的二叉搜索树。F(i, n) 等于左右子树的笛卡尔积。故
$F (i, n) = G (i - 1) * G (n - i)$
于是
$\sum^n_{i=1}G(i - 1) * G(n - i)$

G(2) = G(0) * G(1) + G(1) * G(0)
G(3) = G(0) * G(2) + G(1) * G(1) + G(2) * G(0)
G(4) = …
根据转移方程，从小到大求解即可。

复杂度分析
- 时间复杂度 O(n^2)。两层遍历 O(n^2)
- 空间复杂度 O(n)。

此外，还有一个更数学的方法，G(n) 其实就是卡塔兰数，具体推导这里不展开，感兴趣可以再查阅。

代码

class Solution {
public:
    int numTrees(int n) {
        if (n < 1) {
            return 1;
        }
        vector<int> G(n+1);
        G[0] = 1;
        G[1] = 1;
        for (int i = 2; i <= n; i++) {
            for (int j = 1; j <= i; j++) {
                G[i] += G[j - 1] * G[i - j];
            }
        }
        return G[n];
    }
};