RMS值实际就是方均根值,就是一组统计数据的平方和的平均值的平方根。
RMSE为均方根误差,标示实际值与预测值之间的误差。公式如下:
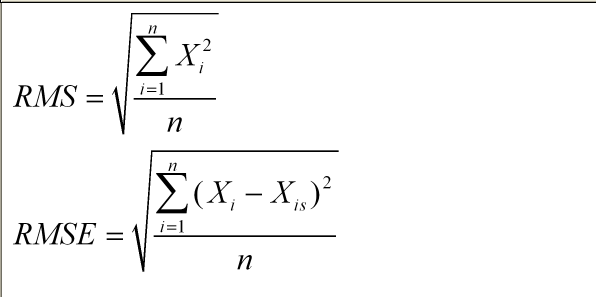
MAE为平均绝对误差

其中X(is)为x(i)的实际值,X(i)为预测值
 本文介绍了RMS(方均根值)的概念及其计算方法,并解释了RMSE(均方根误差)的意义与应用场景,同时对比了MAE(平均绝对误差)与RMSE的区别。
本文介绍了RMS(方均根值)的概念及其计算方法,并解释了RMSE(均方根误差)的意义与应用场景,同时对比了MAE(平均绝对误差)与RMSE的区别。
RMS值实际就是方均根值,就是一组统计数据的平方和的平均值的平方根。
RMSE为均方根误差,标示实际值与预测值之间的误差。公式如下:
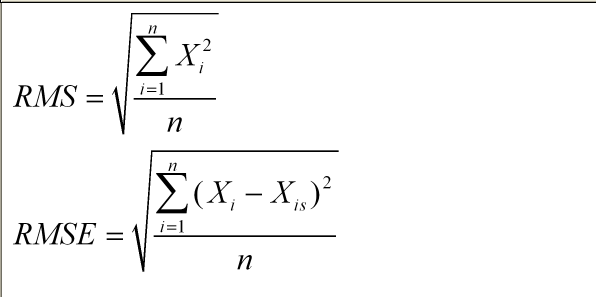
MAE为平均绝对误差

其中X(is)为x(i)的实际值,X(i)为预测值
 988
988

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


