@2018 牛客网暑期ACM多校训练营（第四场）:D Another Distinct Values(打表找规律)

链接：https://www.nowcoder.com/acm/contest/142/D
来源：牛客网
 

Chiaki has an n x n matrix. She would like to fill each entry by -1, 0 or 1 such that r1,r2,...,rn,c1,c2, ..., cn are distinct values, where ri be the sum of the i-th row and ci be the sum of the i-th column.

输入描述:

There are multiple test cases. The first line of input contains an integer T (1 ≤ T ≤ 200), indicating the number of test cases. For each test case:
The first line contains an integer n (1 ≤ n ≤ 200) -- the dimension of the matrix.

输出描述:

For each test case, if no such matrix exists, output ``impossible'' in a single line. Otherwise, output ``possible'' in the first line. And each of the next n lines contains n integers, denoting the solution matrix. If there are multiple solutions, output any of them.

示例1

输入

复制

2
1
2

输出

复制

impossible
possible
1 0
1 -1

 

[题意]

找出一种 放置方式 在  n*n的 矩阵内 保证 任意的行纸和 与 任意的列 之和,以及 行行,列列直间 不一样.

[思路]

dfs 打表, 打n=4

可以发现 奇数没有答案,  偶数, 分块,

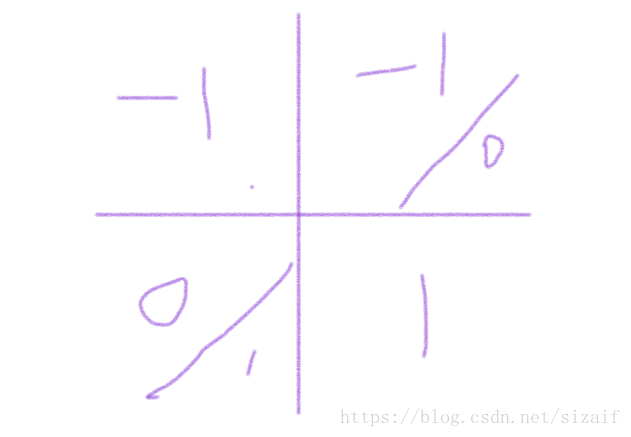
[代码]

#include <bits/stdc++.h>
#include <stdlib.h>
#include <utility>
#define findx(x,b,n) lower_bound(b+1,b+1+n,x)-b
#define FIN      freopen("input.txt","r",stdin)
#define FOUT     freopen("output.txt","w",stdout)
#define SHUT ios_base::sync_with_stdio(false); cout.setf(ios::fixed); cout.precision(20); cout.tie(nullptr); cin.tie(nullptr);
#define lson rt << 1, l, mid
#define rson rt << 1|1, mid + 1, r

#pragma comment(linker, "/STACK:1024000000,1024000000")  // 扩栈
//next_permutation(a+1,a+x) 全排列
#define rep(i,a,n) for(int i=a;i<n;i++)
#define per(i,a,n) for(int i=n-1;i>=a;i--)
#define pb push_back
#define mp make_pair
#define all(x) (x).begin(),(x).end()
#define fi first
#define se second
#define SZ(x) ((int)(x).size())

using namespace std;

typedef vector<int> VI;
typedef long long ll;
typedef pair<int,int> PII;


const double PI=acos(-1.0);
const int INF=0x3f3f3f3f;
const double esp=1e-6;
const int maxn=1e6+5;
const int MOD=16777216;
const int mod=16777216;
int dir[5][2]={0,1,0,-1,1,0,-1,0};


inline void ex_gcd(ll a,ll b,ll &d,ll &x,ll &y){if(!b){ x=1; y=0; d=a; }else{ ex_gcd(b,a%b,d,y,x); y-=x*(a/b);};}
inline ll gcd(ll a,ll b){ return b?gcd(b,a%b):a;}
inline ll exgcd(ll a,ll b,ll &x,ll &y){if(!b){x=1;y=0;return a;}ll ans=exgcd(b,a%b,x,y);ll temp=x;x=y;y=temp-a/b*y;return ans;}
inline ll lcm(ll a,ll b){ return b/gcd(a,b)*a;}
inline ll qpow(ll x,ll n){ll res=1;for(;n;n>>=1){if(n&1)res=(res*x)%MOD;x=(x*x)%MOD;}return res;}
inline ll inv_exgcd(ll a,ll n){ll d,x,y;ex_gcd(a,n,d,x,y);return d==1?(x+n)%n:-1;}
inline ll inv1(ll b){return b==1?1:(MOD-MOD/b)*inv1(MOD%b)%MOD;}
inline ll inv2(ll b){return qpow(b,MOD-2);}

/*********************************head************************/


int n;
int mmps[500][500];
int tts[10][10];


void dfs(int x,int y)
{
    if( y > n+1)
    {
        y = 1;
        x ++;
    }
    if( x == n+1)
    {
        int sux = 0,suy = 0;
        int flag = 0;
        map<int,int>mpp;
        mpp.clear();
        rep(i,1,n+1)
        {
            sux = 0;
            rep(j,1,n+1)
            {
                sux += tts[i][j];
            }
            if(!mpp[sux])
                mpp[sux] = 1;
            else
                flag = 1 ;
        }
        rep(i,1,n+1)
        {
            suy = 0;
            rep(j,1,n+1)
            {
                suy += tts[j][i];
            }
            if(!mpp[suy])
                mpp[suy] = 1;
            else
                flag = 1;
        }
        if(!flag)
        {
            rep(i,1,n+1)
            {
                rep(j,1,n+1)
                {
                   printf("%3d ",tts[i][j]);
                }
                cout<<endl;
            }
            cout<<endl;
            cout<<"//////////////////"<<endl;
            cout<<endl;
        }
        return ;
    }

    rep(k,-1,2)
    {
        tts[x][y] = k;
        dfs(x,y+1);
    }
}
int main()
{
    int t;
    scanf("%d",&t);
    while(t--)
    {
        scanf("%d",&n);
        if(n%2==1)
        {
            cout<<"impossible"<<endl;
            continue;
        }
        else
            cout<<"possible"<<endl;
        memset(mmps,0,sizeof(mmps));
        rep(i,1,n/2+1)
        {
            rep(j,1,n+1)
                mmps[i][j] = -1;
        }
        int c ;
        rep(i,2,n/2+1)
        {
            c = i-1;
            for(int j = n;c>0;j--,c--)
                mmps[i][j] = 0;
        }
        rep(i,n/2+1,n+1)
        {
            rep(j,1,n/2+1)
                mmps[i][j] = 0;
        }
        int  k = n/2;
        for(int i = n;i>n/2+1;i--)
        {
            c = --k;
            for(int j = n/2;c>0;j--,c--)
                mmps[i][j] = 1;
        }
        rep(i,n/2+1,n+1)
        {
            rep(j,n/2+1,n+1)
                mmps[i][j] = 1;
        }
        rep(i,1,n+1)
        {
            rep(j,1,n+1)
            {
                printf("%d%c",mmps[i][j],j==n?'\n':' ');
            }
        }
    }

    return 0;
}